Производные основных элементарных функций 3 страница
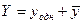
Для нахождения 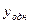 составим характеристическое уравнение
составим характеристическое уравнение 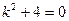 , имеющее комплексные корни
, имеющее комплексные корни 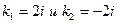 . В этом случае общее решение однородного уравнения ищем в виде
. В этом случае общее решение однородного уравнения ищем в виде
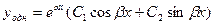 (4)
(4)
где 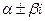 - комплексные корни характеристического уравнения. Подставим в (4)
- комплексные корни характеристического уравнения. Подставим в (4) 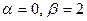 , имеем:
, имеем:
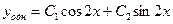
Для нахождения частного решения 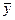 неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция
неоднородного дифференциального уравнения воспользуемся следующей теоремой: если правая часть неоднородного уравнения есть функция 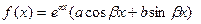 и числа
и числа 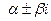 не являются корнями характеристического уравнения, то существует частное решение
не являются корнями характеристического уравнения, то существует частное решение 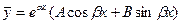 . Если же числа
. Если же числа 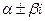 являются корнями характеристического уравнения, то существует частное решение
являются корнями характеристического уравнения, то существует частное решение 
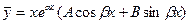 .
.
Применяя эту теорему при 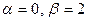 , имеем:
, имеем:
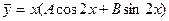 .
.
Дважды дифференцируя последнее равенство, находим 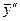 :
:
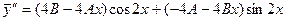
Подставив в данное уравнение 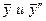 , получим:
, получим:
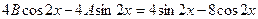 ,
,
Откуда 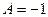 ,
, 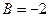 .
.
Следовательно, 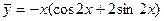 и
и
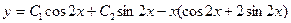
Найдем 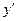 :
:
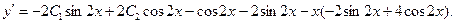
Используя начальные условия, получим систему
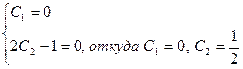
Следовательно, 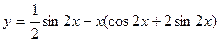 есть искомое частное решение данного дифференциального уравнения.
есть искомое частное решение данного дифференциального уравнения.
Задачи № 91-110; 111-130
Данные задачи относятся к теме «Числовые и степенные ряды». Рассмотрим предварительно следующие вопросы:
1. Понятие числового ряда.
Члены числовой последовательности, соединенные знаком (+) или (-), образуют числовой ряд вида: 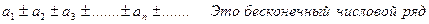
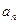 - общий член, где n – порядковый номер члена.
- общий член, где n – порядковый номер члена.
Другая форма записи числового ряда 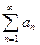
2. Понятие частичной суммы числового ряда и суммы ряда.
Частичной суммой 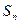 называется сумма первых
называется сумма первых 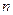 членов.
членов. 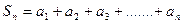 . Конечный предел частичных сумм числового ряда при
. Конечный предел частичных сумм числового ряда при 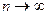 называется суммой ряда
называется суммой ряда 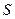 .
. 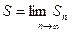 .
.
3. Какой числовой ряд называется сходящимся?
Если числовой ряд имеет сумму 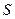 , то ряд является сходящимся. Если же
, то ряд является сходящимся. Если же 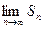 не существует или равен
не существует или равен 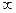 , то числовой ряд – расходящийся и суммы не имеет.
, то числовой ряд – расходящийся и суммы не имеет.
4. Необходимый признак сходимости числового ряда. Достаточные признаки сходимости для знакоположительных рядов: признак сравнения, признак Даламбера, интегральный признак Коши.
Теорема. Если числовой ряд сходится, то предел его общего члена при 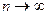 равен 0, т.е.
равен 0, т.е. 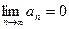 .
.
Необходимый признак сходимости не является достаточным. Поэтому для исследования числовых рядов на сходимость существуют достаточные признаки.
Признак сравнения. Даны два числовых ряда с положительными членами 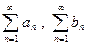 . Если, начиная хотя бы с некоторого номера
. Если, начиная хотя бы с некоторого номера 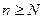 , выполняется
, выполняется 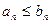 , то:
, то:
1) из сходимости ряда 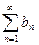 следует сходимость ряда
следует сходимость ряда 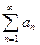 ,
,
2) из расходимости ряда 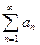 следует расходимость ряда
следует расходимость ряда 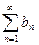
Признак Даламбера. Дан ряд с положительными членами 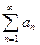 . Если существует предел отношения последующего члена к предыдущему при
. Если существует предел отношения последующего члена к предыдущему при 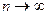 , равный
, равный 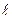 , т.е.
, т.е. 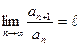 , то:
, то:
1) при 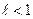 ряд сходится
ряд сходится
2) при 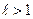 ряд расходится
ряд расходится
3) при 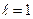 вопрос остается открытым
вопрос остается открытым
5. Признак Лейбница о сходимости знакочередующегося ряда.
Числовой ряд вида 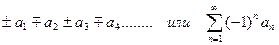 называется знакочередующимся.
называется знакочередующимся.
Признак Лейбница. Если: 1) члены знакочередующегося ряда 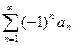 убывают по абсолютной величине, т.е.
убывают по абсолютной величине, т.е. 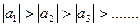 и 2)
и 2) 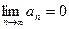 , то такой ряд сходится и его сумма
, то такой ряд сходится и его сумма 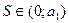 .
.
6. Понятие степенного ряда и области его сходимости.
Степенным рядом называется функциональный ряд:
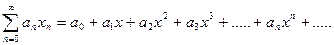 ;
;
где 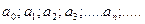 - коэффициенты ряда,
- коэффициенты ряда, 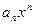 - общий член ряда – степенная функция.
- общий член ряда – степенная функция.
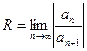 - радиус сходимости; (-R;R) – интервал сходимости.
- радиус сходимости; (-R;R) – интервал сходимости.
Интервал (-R;R) c включением одного или двух его концов называется областью сходимости степенного ряда.
7. Разложение в ряд Маклорена функций: 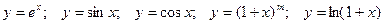
Всякая функция f(x) бесконечно дифференцируемая в интервале (-R;R) разлагается в ряд Маклорена:
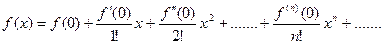 .
.
Интервал (-R;R) – интервал сходимости ряда Маклорена.
8.Применение степенных рядов в приближенных вычислениях.
На практике приходится прибегать к приближенным вычислениям функций; определенных интегралов; при решении дифференциальных уравнений. В этих случаях функцию разлагают в степенной ряд Маклорена, а ряд заменяют суммой конечного числа членов с требуемой точностью. Точность оценивается с помощью первого отброшенного члена.
С помощью рядов составлены таблицы тригонометрических функций; таблицы логарифмов; таблицы, применяемые в теории вероятностей и математической статистике.
Рассмотрим задачи:
Задача 1. Написать первые три члена ряда 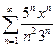 , найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
, найти интервал сходимости ряда и исследовать его сходимость на концах интервала.
Решение. Беря последовательно 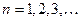 , запишем данный ряд в виде:
, запишем данный ряд в виде:
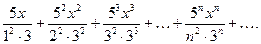
Для нахождения области сходимости ряда применим признак Даламбера
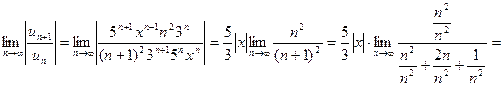
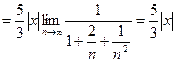
Данный ряд сходится абсолютно при тех значениях х, которые удовлетворяют неравенству 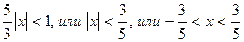
Исследуем сходимость ряда на концах полученного интервала. При 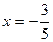 данный ряд принимает вид
данный ряд принимает вид 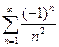 .
.
Последний ряд является знакочередующимся; абсолютная величина его члена стремится к нулю при 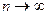 и члены убывают по абсолютной величине. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит,
и члены убывают по абсолютной величине. Следовательно, по признаку Лейбница сходимости знакочередующихся рядов этот ряд сходится. Значит, 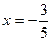 принадлежит области сходимости данного ряда.
принадлежит области сходимости данного ряда.
При 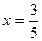 данный ряд принимает вид
данный ряд принимает вид 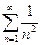 . Исследуем сходимость этого ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл
. Исследуем сходимость этого ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл
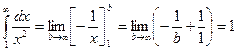
Так как несобственный интеграл сходится, то сходится и исследуемый ряд. Значит, при 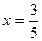 исходный ряд сходится.
исходный ряд сходится.
Таким образом, 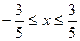 - область сходимости данного ряда.
- область сходимости данного ряда.
Задача 2.Вычислить 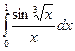 с точностью до 0,001.
с точностью до 0,001.
Решение. Представим подынтегральную функцию в виде степенного ряда.
Заменив x в разложении функции 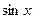 на
на 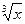 имеем:
имеем:
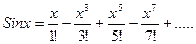 .
.
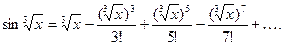
Тогда
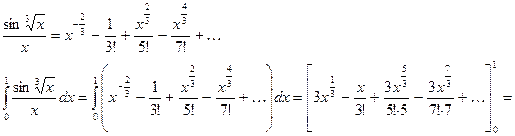
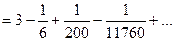
Полученный знакочередующийся ряд удовлетворяет условию теоремы Лейбница. Так как четвертый его член по абсолютной величине меньше 0,001, то для обеспечения заданной точности достаточно взять первые три члена. Тогда
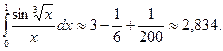

Тренировочные задания
1. Найти указанные пределы
1. 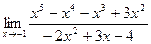 2.
2. 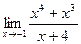
3. 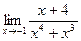 4.
4. 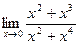
5. 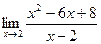 6.
6. 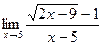
7. 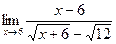 8.
8. 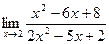
9. 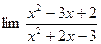 10.
10. 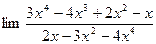
а) 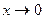 а)
а) 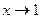
б) 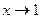 б)
б) 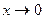
в) 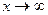 в)
в) 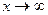
11. 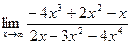 12.
12. 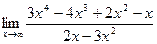
13. 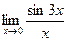 14.
14. 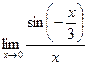
15. 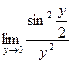 16.
16. 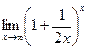
17. 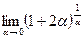 18.
18. 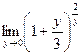
2. Найти производные и дифференциалы функции
1. 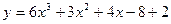 13.
13. 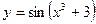
2. 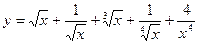 14.
14. 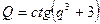
3. 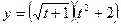 15.
15. 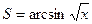
4. 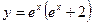 16.
16. 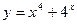
5. 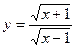 17.
17. 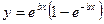
6. 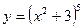 18.
18. 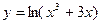
7. 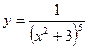 19.
19. 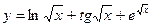
8. 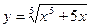 20.
20. 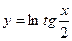
9. 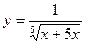 21.
21. 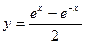
10. 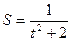 22.
22. 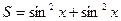
11. 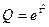 23.
23. 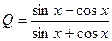
12. 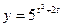 24.
24. 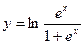
3. Найти полные дифференциалы для данных функций



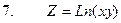
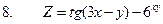
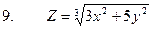
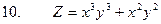
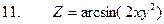
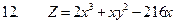
4.Найти неопределенные и определенные интегралы.
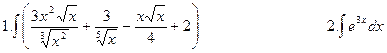







ПРАВИЛО ВЫБОРА ВАРИАНТА
Вариант контрольной работы определяется по таблице в зависимости от двух последних цифр номера шифра личного дела студента. В колонке таблицы по вертикали расположены цифры от 0 до 9, каждая из которых - предпоследняя цифра номера шифра. В верхней строке по горизонтали размещены так же цифры от 0 до 9, каждая из которых - последняя цифра шифра.
Пересечение вертикальной и горизонтальной линий определяет номера заданий контрольной работы. Например, по последним двум цифрам номера шифра «78» находят вариант контрольной работы на пересечении строки с цифрой 7 и столбца с цифрой 8. Для контрольной работы №1 это номера:5, 11, 27, 40, 41, 58, 70, 79, 82.
ТАБЛИЦА ВЫБОРА ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ №2
