Без ограничений и неотрицательность переменных

Начнем с изучения методов решения задач ВП без ограничений. Задача НП называется задачей без ограничений, если она не содержит условий, ограничивающих область изменений переменных. Такая задача имеет вид

Z = f (x₁ ,x₂ ,…, x_n ) max.

(3.1)

Необходимое условие экстремума целевой функции f (x₁ ,x₂ ,…, x_n ) заключается в следующем. Пусть f дифференцируема и имеет экстремум в некоторой точке. Тогда в этой точке будут верны такие равенства:

. . . ,

Точки, которые удовлетворяют условию (3.8),Ж называются стационарными. В общем случае система (3.8) может иметь множество решений. Система может быть сложной и ее решение не всегда возможно.

Для случая выпуклой (вогнутой) функции f система если имеет решения, то только одно. Оно будет доставлять функции f максимум, если f выпукла, доставлять минимум, если f вогнута.

Теперь рассмотрим вопрос о решении задачи выпуклого программирования в случае неотрицательности переменных.

(3.2)

Задача вида

Z = f (x₁ ,x₂ ,…, x_n ) max

x_j ≥ 0 ; j=1,2,…,n,

где f (x₁ ,x₂ ,…, x_n ) - выпуклая (вогнутая) функция, называется задачей ВП с неотрицательными переменными.

Сформулируем условия для определения наибольшего значения функции f в задаче(3.3). Внутри области (x_j 0) необходимым условием экстремума является равенство нулю частных производных функции f : =0. На границе области (x_j = 0) частные производные удовлетворяют условию ≤ 0, если f вогнутая функция.

Примеры возможных решений задачи максимизации функции одной неотрицательной переменной иллюстрируют все возможные решения задачи в одномерном случае(рис.1-3). Если решение внутри области(x₀ > 0), то производная =0 .Рассмотрим решение задачи максимизации функции f. Предположим, что ее решение x₀ находится внутри области определения. В этом случае производная функции f в точке максимума x₀ равна нулю. Данная ситуация отражена на рис. 1

y y y

f_x'(x₀)=0 ≤0 < 0

0 x₀>0 x 0 x₀=0 x 0 x₀=0 x

^{рис. 1 рис. 2 рис. 3}

Возможны также случаи расположения решения x₀ на границе области. При нахождении наибольшего значения в этом случае производная функции f в точке x₀ может быть неположительной (рис.2). Такая ситуация возникает при выпуклости максимизируемой функции. Производная функции f в точке x₀ может быть и отрицательной (рис. 3).Это будет в случае, когда максимизируемая функция будет вогнутой.

Все случаи расположения решения x₀ на границе области определения функции f можно обобщить в виде неравенства: ≤0.

Все эти случаи можно отразить в виде равенства нулю произведения x₀ на ,то есть в виде равенства x₀ = 0.

Следовательно, для одномерной функции необходимое условие экстремума

x₀ = 0.

Аналогично рассуждая, можно сформулировать необходимое условие экстремума функции n переменных, оно будет иметь вид x_j 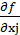=0; j=1,2,…,n,

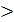где x_j ≥ 0, ≤ 0. Причем, если x_j 0, то 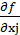=0, если, x_j = 0, то 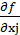≤ 0.

Аналогичным будет подход и к решению задачи выпуклого программирования в случае ограничений в виде равенств.