Параметры вынужденных колебаний. Резонанс

Вынужденные колебания совершаются с частотой изменения вынуждающей силы, но при этом амплитуда колебаний и сдвиг фаз колебаний относительно вынуждающей силы зависят от разности собственной частоты колебаний и частоты вынуждающей силы ( ).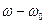

Для амплитуды выполняется зависимость:

,

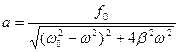а для разности фаз:

.

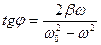Резонансом называется резкое возрастание амплитуды колебаний при приближении частоты вынуждающей силы к собственной частоте. Особенно сильно резонанс проявляется при малом затухании β.

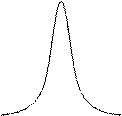
A Резонансная частота это такая частота

вынуждающей силы при которой амплиту-

да вынужденных колебаний будет макси-

мальна:

.

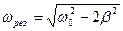Соответственно резонансная амплитуда

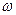оказывается равной:

рис. 29 Резонанс .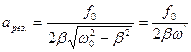

Здесь ω′ , как и выше, обозначена частота затухающих колебаний:

.

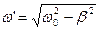При 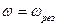тангенс разности фаз вынужденных колебаний и вынуждающей силы оказывается равным 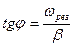. И при малом значении затухания β ( 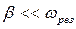) 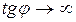, а это означает, что .

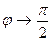Волны. Уравнение волны.

Волновой процесс – колебания, распространяемые в среде (в пространстве). При этом направление колебаний и направление распространения волны могут совпадать, а могут быть взаимно перпендикулярны. Если направление колебаний совпадает с направлением распространения волны, то такие волны называются продольными. А в случае, когда колебания совершаются в направлении перпендикулярном распространению волны – поперечными.

Волновым фронтом называют геометрическое место точек, до которых к настоящему моменту дошел волновой процесс.

Волновая поверхность геометрическое место точек, колеблющихся в одной фазе.

Если волновые поверхности (и волновой фронт) представляют собой плоскости, то такие волны называются плоскими волнами.

Соответственно у сферических волн волновые поверхности имеют форму сферы.

При описании волнового процесса смещение из положения равновесия принято обозначать буквой ξ (кси), поскольку координата x связана с информацией о распространении волны. Соответственно, амплитуду колебаний будем обозначать ξ_0.

Если в точке с координатой x в результате распространения плоской волны возникают колебания, описываемые обычным гармоническим уравнением колебаний 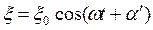, то необходимо учесть, что начались они только тогда, когда до этой точки дошла волна. Поэтому из начальной фазы следует вычесть отставание фазы, возникшее за время Δt, затраченное волной на преодоление этого расстояния:

.

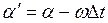Δt зависит от скорости распространения волны υ: 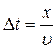. Значит, колебания в точке с координатой x подчиняются закону:

.

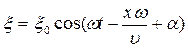Отношение 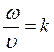называется волновым числом и с помощью него волновой процесс записывается уравнением

,

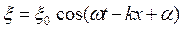которое называется уравнением плоской волны. Данное уравнение дает описание волны в случае, когда волна распространяется вдоль оси x (одномерный случай). Если плоская волна распространяется в произвольном направлении, задаваемом вектором (трехмерный случай), то уравнение плоской волны будет выглядеть так:

.

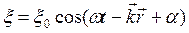Здесь вектор 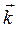- волновой вектор, проекциями которого на оси являются соответствующие волновые числа:

.

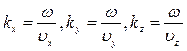В уравнении сферической волны необходимо учесть уменьшение амплитуды обратно пропорционально расстоянию, пройденному волной:

.
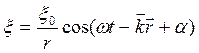