Универсальный вертикальный питатель магазинного типа

Универсальный вертикальный питатель [68] рис.1.17 состоит из основания 1, через которое проходит штанга 2 с кулачком 3, приёмника заготовок 8, отсекателя 10, опирающегося на подшипник 7, установленный на оси 14. Отверстия в приёмнике 8 и отсекателе 10 имеют такое же расположение, как в

плите 19. К отсекателю 10 прикреплена планка 5 со штырём 4, а так же штифт 21, связанный с пружиной 9, которая соединена с приёмником 8. На подшипниках 13, 15 расположена втулка 17, которая через подпружиненный фрикционный механизм 6 связана с отсекателем 10. На втулке 17 жёстко закреплён магазин, состоящий из двух пластин – верхней 16 и нижней 11, выполненный в виде храповика с собачкой 12, в отверстиях которых вставлены трубки 18, расположенные по концентрическим окружностям. Центры отверстий трубок на средней окружности смещены на угол относительно центров отверстий трубок на внутренней окружности, а центры отверстий на средней окружности смещены

Рис. 1.17.

на угол относительно отверстий трубок наружной окружности. Между магазином и отсекателем закреплена неподвижная плита 19. Отверстия в плите 19 по окружности смещены относительно отверстий отсекателя, чтобы в исходном положении заготовки из трубок 18 через отверстие плиты 19 не попали в отверстия отсекателя 10.

После заполнения магазина заготовками его поворачивают до тех пор, пока заготовки из трубок 18 не попадут в отверстия плиты 19. При перемещении штанги 2, приводимой в движение от рабочего органа станка или сборочного автомата, кулачок 3 через штырь 4 и планку 5 поворачивает отсекатель 10 до совмещения его отверстий с отверстиями плиты 19. Заготовки поступают в отверстия отсекателя 10. При этом магазин, удерживаемый собачкой 12, не поворачивается. При опускании штанги 2 отсекатель 10 под действием пружины 9 возвращается в исходное положение, совмещая свои отверстия с отверстиями приёмника 8, заготовки проваливаются в приёмник и по лоткам 20 попадают в рабочую зону. Магазин, заклиниваемый новыми заготовками, попавшими из трубок в отверстия неподвижной плиты 19, не поворачивается. Это происходит до тех пор, пока последние заготовки из трубок 18, совмещённых с отверстиями плиты 19, не выпадут в отверстия отсекателя 10. После этого при возвращении отсекателя в начальное положение, благодаря фрикционному механизму 6, движение через втулку 17 передаётся магазину, который поворачивается до тех пор, пока заготовки из трубок средней концентрической окружности не поступают в отверстия плиты 19 и т.д. Максимальное число одновременно выдаваемых заготовок определяется числом отверстий на одной концентрической окружности плиты 19, отсекателя 10, приёмника 8. Устанавливая заглушки на отверстия только на плите 19, можно регулировать число выдаваемых заготовок.

Время подачи заготовок из вертикального питателя равно:

,

где - время срабатывания отдельных механизмов.

1 этап движения. Выпадение заготовки в отсекатель.

Кинематическая схема согласно рис. 1.17 приведена на рис. 1.18, где а – заготовка.

Воспользуемся основным уравнением динамики и будем учитывать только силу веса заготовки . Минимальная скорость выпадания будет у последней заготовки магазина. В проекции на ось движения уравнение запишется:

,

где - ускорение свободного падения; - проекция ускорения.

Рис. 1.18.

Дважды интегрируя уравнение при нулевых начальных условиях окончательно получим время выпадания заготовки:

, (1.86)

где - длина или диаметр шаровой заготовки.

2 этап движения. Поворот отсекателя на позицию выдачи заготовок – этап движения 2а и возвращение его в исходное положение – этап движения 2б.

Отсекатель рис.1.19 под действием внешних сил, от кулачка или пневмоцилиндра, поворачивается на требуемый угол, а возвращается в исходное положение под действием пружины.

При разработке устройств наряду с решением задачи надёжного функционирования с требуемой точностью решается задача обеспечения максимальной производительности, т.е. решение задачи определения предельных режимов работы.

Рис. 1.19.

Определение жёсткости пружины отсекателя

Найдём жёсткость пружины из необходимого условия надёжного возвращения отсекателя в исходное положение:

, (1.87)

где - момент силы пружины; - соответственно моменты трения заготовок торчащих из магазинов на первой, второй и третьей окружностях, упирающихся в плоскость отсекателя; - момент трения фрикциона об отсекатель.

Для обеспечения надёжного функционирования фрикциона необходимо, чтобы его момент был больше моментов трения заготовок об отсекатель.

.

Запишем равенство:

, (1.88)

где - коэффициент запаса момента ( =1,3).

Запишем (1.87) в виде равенства, подставим в него (1.88) и значения каждого составляющего выражения:

(1.89)

где - сила пружины отсекателя; - коэффициент запаса момента ( =1,3); - вес заготовки; - число заготовок в трубке магазина; - число трубок (магазинов) по окружности; - коэффициент трения; - радиус отсекателя; 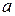- длина рычага пружины отсекателя; - соответственно радиусы расположения трубок по внутренней окружности, средней и наружной.

В момент приведения отсекателя в исходное положение сила пружины равна: ,

где - жёсткость пружины; - величина предварительного натяжения пружины, которым задаются.

Из (1.89) с учётом последнего выражения найдём минимальную жёсткость пружины отсекателя:

. (1.90)

Этап движения 2б.

Найдём время приведения отсекателя в исходное положение.

Воспользуемся дифференциальным уравнением вращательного движения [13] отсекателя:

, (1.91)

где - момент инерции отсекателя относительно центра 0; - вектор углового ускорения; - главный вектор внешних сил, действующих на систему.

В проекции на ось вращения с учётом всех действующих сил уравнение (1.91) запишется:

, (1.92)

где (1.93)

В первом приближении считаем удлинение пружины « » в растянутом положении линейным размером.

После преобразований уравнение (1.92) с учётом (1.93) примет вид:

. (1.94)

Обозначим коэффициент при ‑ , а постоянный член правой части уравнения - , получим:

. (1.95)

Решение данного уравнения нужно искать в виде суммы решений однородного дифференциального уравнения и частного решения данного уравнения:

. (1.96)

Решение однородного уравнения запишется:

; (1.97)

где - постоянные интегрирования, которые находятся из начальных условий.

Частные решения данного уравнения нужно искать в виде:

. (1.98)

Тогда подставляя и в уравнение (1.95) найдём частное решение:

. (1.99)

Отсюда . (1.100)

Подставим (1.97) и (1.100) в уравнение (1.96):

.

Найдём постоянные интегрирования, а для этого сформируем второе уравнение:

.

Запишем начальные условия движения отсекателя в исходное положение:

При .

Окончательно получим закон движения отсекателя:

. (1.101)

Проще найти время поворота отсекателя не аналитическим, а графическим способом. В уравнение (1.101) подставляем время и строим кривую. На графике заданному углу поворота отсекателя будет соответствовать время (рис.1.20).

Рис. 1.20.

Определение силы пневмоцилиндра (кулачка)

Найдём силу пневмоцилиндра или кулачка, которая надёжно обеспечит поворот отсекателя на требуемый угол .

Необходимое условие надёжного поворота:

. (1.102)

Сила пружины в крайнем положении после поворота равна:

.

С учётом правой части выражения (1.89), выражение (1.90) (1.102) запишется:

,

где - коэффициент запаса момента ( =1,2).

Окончательно сила пневмоцилиндра равна:

. (1.103)

С другой стороны сила пневмоцилиндра находится исходя из параметров поршня:

, (1.104)

где - давление воздуха в магистрали; - диаметр поршня.

Отсюда находим диаметр поршня.

Определение предельной угловой скорости движения отсекателя

Найдём предельную угловую скорость движения отсекателя, при которой в момент удара об упор В (рис.1.19) стержень испытывал бы напряжения изгиба только в пределах упругих деформаций.

Воспользуемся дифференциальным уравнением вращательного движения [13] (1.91). Спроектируем его на ось вращения, один раз проинтегрируем и рассмотрим случай удара, когда учитывается только сила удара.

, (1.105)

где - угловые скорости в конце и начале движения; - момент силы удара рычага об упор В; - время удара.

В конце удара =0, тогда (1.105) примет вид:

. (1.106)

Считаем, что работы силы удара и силы медленного нагружения рычага при одинаковом изгибе одинаковы;

тогда , (1.107)

где - изгибающий момент рычага.

; .

Окончательно: (1.108)

Известно [54], что .

Отсюда . (1.109)

, (1.110)

где - диаметр рычага.

Величина прогиба стержня равна:

, (1.111)

где - изгибающая сила рычага; - модуль упругости материала рычага; - полярный момент инерции сечения рычага:

. (1.112)

Длина дуги изгиба равна:

.

Отсюда . (1.113)

Подставим (1.108, 1.109, 1.110, 1.116, 1.112 и 1.113) в выражение (1.107) и после преобразований получим:

.

Выделим из последнего выражения правую часть уравнения (1.106), подставим в него и найдём предельную угловую скорость движения отсекателя, при которой стержень будет испытывать только упругие деформации.

. (1.114)

Для обеспечения требуемой скорости (1.114) поворота отсекателя необходимо на шток пневмоцилиндра поставить пружину торможения.

Пример 1.1. Определить предельную частоту вращения отсекателя при торможении его движения ударом стержня об неподвижный упор (рис.1.19).

Данные для расчёта приведены в таблице 1.1.

Таблица 1.1.

Материал стержня и упора сталь 45	Параметры стержня	Параметры отсекателя
Предел прочности на изгиб	Модуль упругости материала	Диаметр	Длина	Диаметр	Вес	Момент инерции
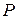(кг/см2)	Е (кг/см2)	(см)	(см)	(см)	(см)	(кг×см×с2)
	2×106				5,39	3,2076

Находим предельную угловую скорость вращения отсекателя:

=0,128 с^-1.

Определяем частоту вращения отсекателя:

=1.225 об/мин.

Определение жёсткости пружины пневмоцилиндра

Воспользуемся принципом Даламбера [13]. Расчётная схема соответствует рис. 1.19, где - сила пневмоцилиндра и добавится противодействующая сила – сила пружины пневмоцилиндра.

Следует заметить, что предельная угловая скорость отсекателя будет в случае, когда выдана последняя заготовка из магазина, а остальные магазины пусты.

Запишем выражение моментов сил в проекции на ось вращения в момент начала удара.

, (1.115)

где ; - момент трения в подшипниках отсекателя (можно пренебречь); (жёсткость С берётся из выражения (1.90); - момент от пружины пневмоцилиндра ( ); - момент сил инерции ( ).

Считаем, что движение отсекателя – равноускоренное.

Тогда - угол поворота отсекателя .

Подставляя в (1.115) все составляющие моменты и найдём жёсткость пружины пневмоцилиндра:

. (1.116)

Определение времени поворота отсекателя

Воспользуемся дифференциальным уравнением вращательного движения [13]. С учётом действующих сил: - силы пневмоцилиндра; - силы пружины пневмоцилиндра; - силы пружины отсекателя; 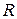- силы вязкого трения, а так же рассматривая случай, когда все магазины опустошены и выдаётся порция последних заготовок дифференциальное уравнение в проекции на ось вращения запишется:

(1.117)

где берётся из выражения (1.116), а С – из (1.114).

После преобразования уравнение (1.117) примет вид:

(1.118)

Обозначим: коэффициент при - 2 ; при - , а постоянный член правой части уравнения - , получим:

. (1.119)

Решения уравнения нужно искать в виде:

.

Решение однородного дифференциального уравнения определяется соотношением и 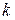. Рассматриваем случай большого сопротивления, когда > .

,

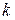где - круговая частота с учётом сопротивления .

Частное решение нужно искать в виде:

,

где - постоянный член.

Тогда ;

.

Решение уравнения (1.119) запишется:

. (1.120)

Сформируем второе уравнение, взяв производную от предыдущего:

.

Запишем начальные условия.

При .

Из уравнения изменения угла поворота имеем:

.

Из уравнения изменения скорости:

.

После преобразований запишем постоянные интегрирования:

.

Подставляя постоянные интегрирования в уравнение (1.120) получим закон движения отсекателя при выдаче заготовок в приёмник.

. (1.121)

Время поворота отсекателя находим из графической зависимости, построенной по уравнению (1.121) путём подстановки текущих значений времени движения.

Время поворота отсекателя будет соответствовать углу его поворота .

3 этап движения. Выпадание заготовки в приёмник.

По аналогии с первым этапом движения:

,

где - высота приёмника.