Связь параметров колебательной системы с периодом колебаний. Энергия колебательной системы с одной степенью свободы

В предыдущих параграфах данной главы были введён параметр колебательной системы w – круговая или циклическая частота и частота колебаний n, связанные между собой соотношением 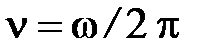. Для строгого выяснения физического смысла этих величин выразим их через период колебания.

Периодом колебаний называют промежуток времени, по истечении которого колебание повторяется, то есть колеблющаяся точка, тело проходит те же положения и в том же направлении (см. рис. 3.2.). Аналитически это может быть записано так х(t + n×Т) = х(t); здесь n – целое число (периодов), Т – период колебаний, t – промежуток времени, через который нас интересует положение движущейся точки, тела. Аналитическая запись может быть прочитана так, через произвольное целое число периодов тело будет двигаться так же, как и в данный момент времени. Уравнение движения примет вид: 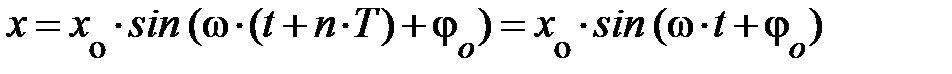. Поскольку синусы двух аргументов равны, если эти аргументы отличаются на 2p×n, (где 2p – период синуса, косинуса, n – целое число этих периодов), то возможна следующая запись 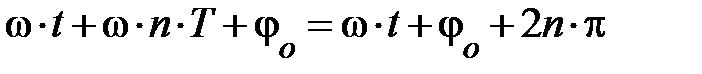. Из равенства фаз следует связь между периодом и круговой частотой 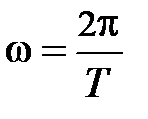, которая показывает число полных колебаний совершаемых за 2p секунд. Круговая частота измеряется в радианах за секунду. Частота колебаний равная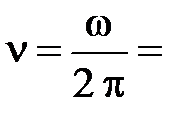 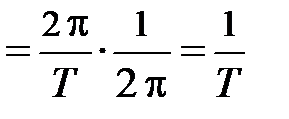показывает, сколько колебаний совершается за одну секунду. Единицей измерения частоты является герц (Гц). Если период колебаний Т = 1 с, то частота n = 1 Гц, что означает – через 1 с тело проходит те же положения и в том же направлении (см. рис. 3.2.).

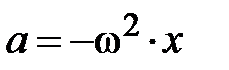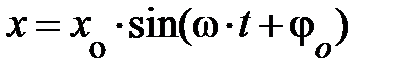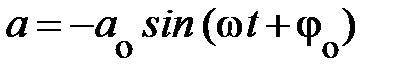Подводя итог сказанному выше, обратим внимание на следующее. Всякое колебательное движение есть движение, происходящее с ускорением, поэтому на колеблющееся тело должна действовать сила, сообщающая это ускорение. Направление силы совпадает с направлением ускорения, а вектор ускорения при гармоническом колебании всегда направлен к положению равновесия ; см. рис. 3.3., графики и ; графики всегда противоположны по направлению, что подтверждает – ускорение, как правило, направлено к положению равновесия. Таким образом, тело совершает колебательное движение, если на него действует сила всегда направленная к положению равновесия, а по величине – прямо пропорциональная смещению из этого положения F = ma = – –m× 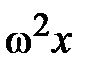= – kx. Для пружинного маятника, представленного на рис. 3.2., период колебаний был получен выше (с. 29). Читатель может попробовать свои силы по преобразованию представленного в предыдущей строчке выражения силы и получить период колебаний пружинного маятника самостоятельно.

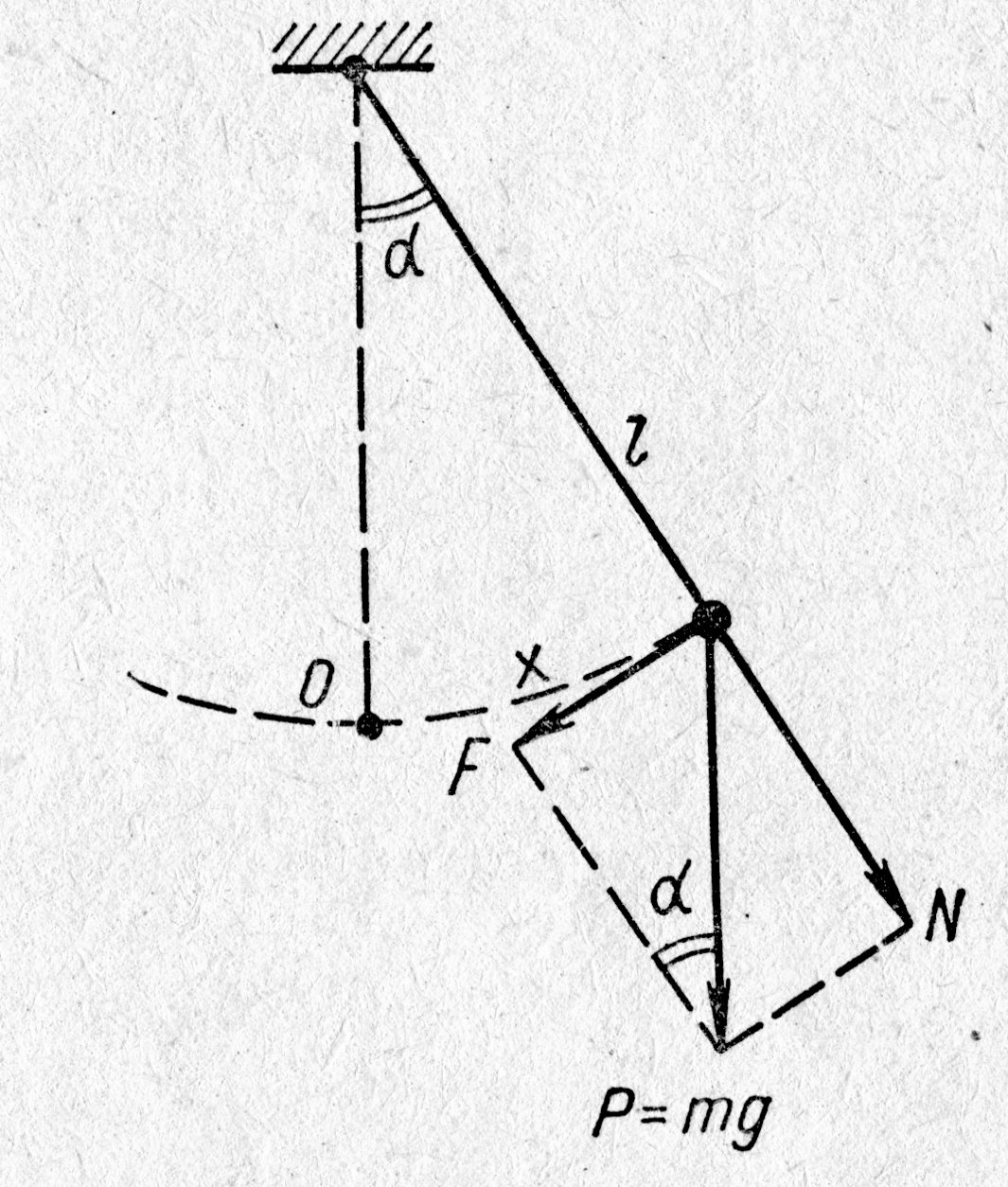
Рис. 3.4.

Fв

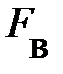Для получения формулы периода колебаний математического мятника, представляющего собой точечное тело массой m, подвешенное к невесомой и нерастяжимой нити длиной l, воспользуемся рис. 3.4.. Возвращающей в состояние равновесия силой является составляющая силы тяжести на направление движения ; она направлена по касательной к траектории движения. При малых углах отклонения от положения равновесия, синус угла a равен его радианной мере и синус угла a запишется 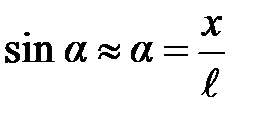, а формула возвращающей силы F = = mg×sina примет вид F @ mg× 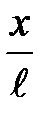. Во втором законе Ньютона последствия возвращающей силы равны произведению массы тела на ускорение колебательного движения. Формула возвращающей силы немедленно принимает вид mg× 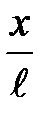= m× 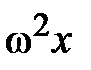. Проведя в последнем равенстве несложные преобразования, читатель самостоятельно может получить аналитическое выражение для периода колебаний математического маятника 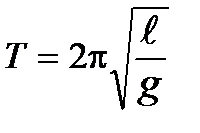. Из формулы следует, параметрами колебательной системы являются длина нити и ускорение свободного падения. В системах такого рода длина нити характеризует инертные свойства маятника (математического, физического) к движению, а именно, к отклонению из состояния равновесия. Ускорение свободного падения в таких системах определяет возвращающее действие в состояние равновесия.

Таким образом, простейшая колебательная система, состоящая из двух тел, является замкнутой консервативной системой, в которой действуют только внутренние силы. Это указывает на то, что работа внутренних сил определяется изменением потенциальной энергии системы и равна изменению кинетической энергии; то есть колебательные движения в механических системах сопровождаются периодическими превращениями кинетической энергии колеблющихся тел в потенциальную энергию взаимодействия частей системы и обратно. Запишем потенциальную энергию системы: 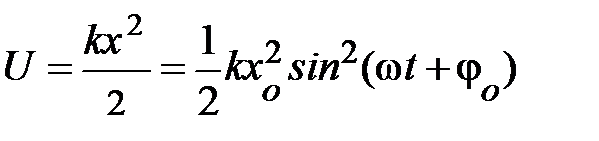, если учесть, что 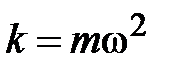, формула энергии запишется 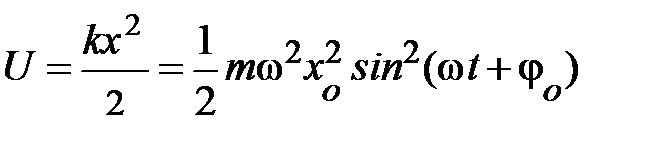. Аналитическое выражение для кинетической энергии имеет вид: 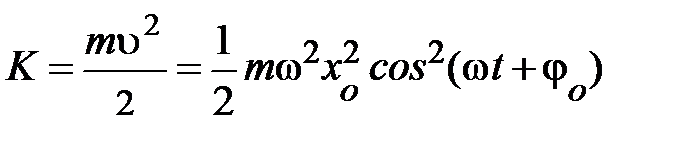. Если читатель проделает простые преобразования, учитывая, что полная энергия системы равна сумме кинетической и потенциальной энергий и примет к вниманию, что 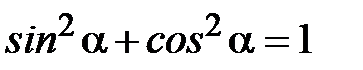, то сможет убедиться – полная энергия системы действительно равна: 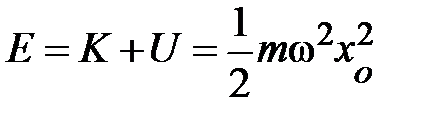. Здесь уместно заметить, в замкнутых системах циклическая частота колебаний не зависит от начальных условий и определяется только параметрами колебательной системы. В приведённых примерах это l, g и k, х.