Свойство 5: (в частности, , )
Проблемы с применением формулы перехода к новому основанию могут возникнуть, если переменная х, относительно которой нужно решить уравнение, стоит в основании логарифма. Приведём пример такой ситуации.
Пример8.Решить уравнение 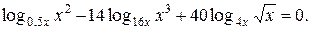
Область определения исходного уравнения – это все положительные числа, кроме 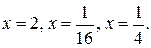 Приводя каждый логарифм к основанию х, получим уравнение
Приводя каждый логарифм к основанию х, получим уравнение 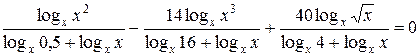 . Его область определения не содержит 1, которая является корнем данного уравнения. Такая ситуация будет возникать в случае, если
. Его область определения не содержит 1, которая является корнем данного уравнения. Такая ситуация будет возникать в случае, если 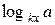 приводится к основанию х.
приводится к основанию х. 
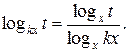 Значение х=1 принадлежит области допустимых значений переменной х в правой части равенства и не принадлежит ей в левой части равенства. Следовательно, число 1 может быть потерянным или посторонним корнем уравнения при использовании формулы перехода к новому основанию логарифма.
Значение х=1 принадлежит области допустимых значений переменной х в правой части равенства и не принадлежит ей в левой части равенства. Следовательно, число 1 может быть потерянным или посторонним корнем уравнения при использовании формулы перехода к новому основанию логарифма.
Аналогичная ситуация возникает, в частности, и при применении формулы 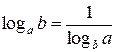 . Запишем её в виде
. Запишем её в виде 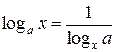 . Число 1 принадлежит области допустимых значений в левой части равенства и не принадлежит ей в правой части, что может привести к потере корня, равного 1, или к приобретению его в качестве постороннего. Приведём пример.
. Число 1 принадлежит области допустимых значений в левой части равенства и не принадлежит ей в правой части, что может привести к потере корня, равного 1, или к приобретению его в качестве постороннего. Приведём пример.
Пример 9.Решить уравнение 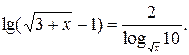
Область определения данного уравнения D=(0;1)È(1;+¥). Преобразуем правую часть уравнения: 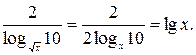 В результате преобразования получим уравнение
В результате преобразования получим уравнение 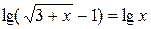 , область определения которого расширилась на 1. Непосредственной подстановкой легко убедиться, что 1 является корнем полученного уравнения, однако, для данного уравнения 1 – посторонний корень.
, область определения которого расширилась на 1. Непосредственной подстановкой легко убедиться, что 1 является корнем полученного уравнения, однако, для данного уравнения 1 – посторонний корень.
Таким образом, при применении формулы 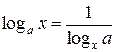 слева направо полезно переходить к совокупности
слева направо полезно переходить к совокупности 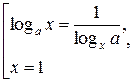 а справа налево – к системе
а справа налево – к системе 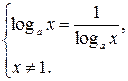
Применение формулы 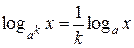 , если переменная х стоит в основании логарифма, а k – чётное число (
, если переменная х стоит в основании логарифма, а k – чётное число ( 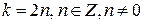 ) также приводит к изменению области определения уравнения. Она принимает вид
) также приводит к изменению области определения уравнения. Она принимает вид 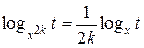 (*). В левой части равенства значения х любые, кроме нуля, а в правой части положительны и отличны от 1. Поэтому формулу (*) слева направо во избежание потери корней целесообразно использовать в виде
(*). В левой части равенства значения х любые, кроме нуля, а в правой части положительны и отличны от 1. Поэтому формулу (*) слева направо во избежание потери корней целесообразно использовать в виде 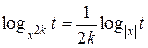 , а при её применении справа налево следует отсеивать возможные посторонние корни. Рассмотрим примеры.
, а при её применении справа налево следует отсеивать возможные посторонние корни. Рассмотрим примеры.
Пример 10.Решить уравнение 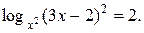
Данное уравнение в области его определения равносильно уравнению 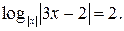 Далее получим систему
Далее получим систему
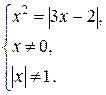
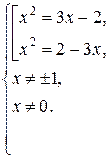

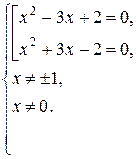
Решения совокупности уравнений: 
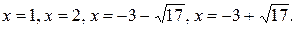 Решения системы:
Решения системы: 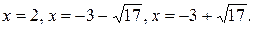
Ответ: 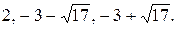
Отметим, что применение свойств 4 и 5 без знака модуля приводит к потере решений.
4.2. Комплекс заданий
Решить уравнение. Ответ.
№ 1. 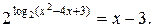 Нет решений.
Нет решений.
№ 2. 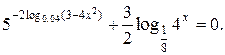
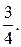
№ 3. 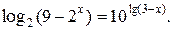 0.
0.
№ 4. 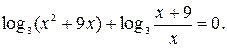 -10.
-10.
№ 5. 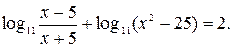 -6; 16.
-6; 16.
№ 6. 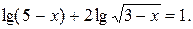
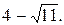
№ 7. 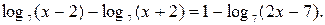 9.
9.
№ 8. 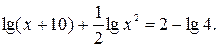
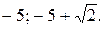
№ 9. 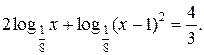
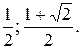
№10. 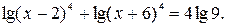
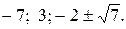
№ 11. 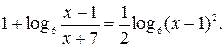 -13.
-13.
№ 12. 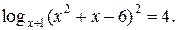 1.
1.
№ 13. 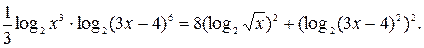 1; 2;
1; 2; 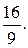
№ 14. 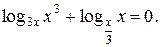 1;
1; 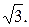
№ 15. 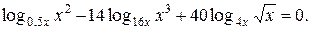 1; 4;
1; 4; 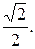
№ 16. 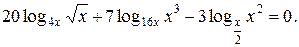 1; 4;
1; 4; 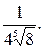
Приведём таблицу использования свойств корней при решении уравнений составленного комплекса.
| Номера свойств | 2 и 3 | |||
| Номера заданий | 1 - 3 | 4 - 7 | 8 -13 | 14 - 16 |
