В последовательном колебательном контуре

С использованием программы FASTMEAN

Цель работы

С помощью программы FASTMEAN смоделировать переходные процессы в последовательном колебательном контуре и исследовать влияние параметров контура на режимы колебаний.

Задание на самостоятельную подготовку к работе

2.1. Изучите теоретические вопросы, связанные с анализом переходных колебаний в последовательном колебательном контуре.

2.2. Каковы особенности анализа колебаний в последовательном колебательном контуре при воздействии прямоугольного импульса?

2.3. В соответствии со своим номером варианта выпишите из табл. 2.1 значения параметров RLC-контура (рис. 2.1) и рассчитайте значение С_кр, при котором возникает критический режим, используя соотношение R_кр= 2 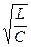. Полученное значение С_кр запишите в табл. 2.3.

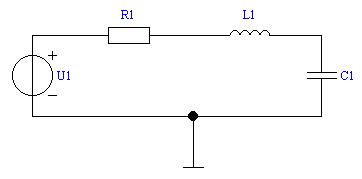
Рис. 2.1

2.4. Рассчитайте и запищите в табл. 2.2 и 2.3 следующие величины:

а) добротность контура при разных значениях емкости С1, С2, С3, С_кр:

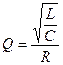
б) значения периода свободных колебаний T_с при С=С2 и С=С3:

T_с = =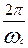

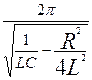
в) корни характеристического уравнения р₁и р₁,величины декремента затухания Δ и логарифмического декремента затухания αT_с при С=С2 и С=С3, используя формулы:

Р_1,2=-α±jω_с, α= ; ; ; ;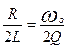

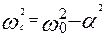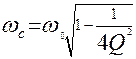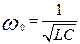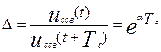; αT_с=lnΔ.

2.5. Рассчитайте и запишите в табл. 2.3 корни характеристического уравнения р₁ и р₂

при С=С1 и С= С_кр:

Р_1,2=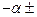

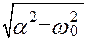
2.6. Покажите на комплексной плоскости расположение корней характеристического уравнения при различных значениях емкости С1, С_кр, С2, С3 с указанием соответствующей величины добротности Q.

Таблица 2.1

Значения параметров RLC-контура

Вариант	Параметры RLC-контура
R, Ом	L, мГн	C1, мкФ	C2, мкФ	С3, мкФ
		3,14		0,05	0,0195
		6,364		0,025	0,0097
		4,46	8,5	0,056	0,014
		6,878		0,04	0,0091
		7,88	6,5	0,032	0,0079
		4,677	4,5	0,026	0,0131
		4,458		0,03	0,0137
		4,606		0,052	0,0136
		4,774	5,2	0,025	0,0128
		6,994	6,2	0,035	0,0089
		2,21		0,055	0,0275
		4,51	4,9	0,027	0,0136

Таблица 2.2

Результаты расчета и анализа на ПК

Предвари- тельный расчет	C, мкс	Q	Tс, мкс	Δ=	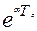αTс	Р1,2=-α±jωс, 1/с
С2
С3
Результаты анализа на ПК		Измеряется по графикам	Вычисляется по данным измерений
Tс		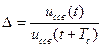αTс=ln Δ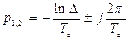
С2
C3

Таблица 2.3

Результаты расчета Q, р₁ и р₂

C,мкФ	Q	Р1=	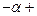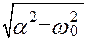Р2=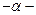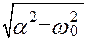
С1 задано
Скр

Задание для работы в компьютерном классе

3.1 Загрузите программу FASTMEAN.

3.2. Постройте на экране дисплея схему последовательного RLC-контура, показанного на рис. 2.1 (приложение, пп.1, 2). Ко входу контура подсоедините источник напряжения. Смоделируйте источник прямоугольных импульсов с t_и = 200 мкс.

Задайте следующие параметры источника напряжения:

«Тип источника – меандр

«Частота (f)» – 1 кГц

«Коэффициент заполнения (К)» – 20%

«Макс.напряжение (Umax)»– 1 В

«Мин.напряжение (Umin)» – 0 В

«Длительность фронта (tfr)» – 1 нс

«Задержка включение (delay)» – 0 пер

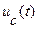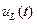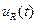3.3. Задайте значения параметров пассивных элементов RLC-контура, пользуясь табл. 2.1. В качестве параметра емкости С выберите значение С1. Рассчитайте временные характеристики , и , для этого выберите в меню «Анализ» → «Переходный процесс». Выведите на дисплей график входного напряжения, а также графики напряжений на элементах R, L и С. Конечное время в меню «Переходный процесс» возьмите равным 400 мкс, число точек 1000.

3.4. Повторите моделирование для емкости С_кр.

3.5. Повторите моделирование при С=С2. На дисплей выведите графики входного напряжения и 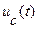. По полученному графику 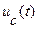с помощью линейки определите величину периода свободных колебаний T_с и значения амплитуд напряжений u_cсв(t) и u_cсв(t+T_c). Рассчитайте величину декремента затухания Δ и занесите Δ и T_с в табл. 2.2. Обратите внимание на то, что при определении u_cсв(t) и u_cсв(t+T_c) в интервале времени 0 ≤ t ≤ t_и значения этих величин, рассчитанные на ПК, составляет сумму собственной и вынужденной составляющих: u_c(t)= u_cсв(t)+ u_cвын(t).

3.6. Повторите п. 3.5 при С=С3.

3.7. Постройте и зарисуйте временные зависимости входного напряжения и 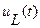при С=С3.

3.8. Постройте и зарисуйте временные зависимости входного напряжения и 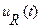при С=С3.

Указания к защите

4.1. Отчет по лабораторной работе должен содержать:

- схему исследуемой цепи;

- расчетные формулы и таблицы с результатами предварительного расчета и анализа на ПК;

- графики рассчитанных на ПК временных зависимосте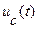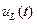й , и 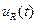с указанием соответствующего режима и величины добротности контура Q;

- заполненные табл. 2.2 и 2.3;

- на комплексной плоскости показать расположение корней характеристического уравнения, рассчитанных согласно пп. 2.4, 2.5;

- выводы о влиянии величины емкости на добротность контура, период собственных колебаний, декремент затухания и длительность переходного процесса;

- графики напряжений.

4.2. Подготовиться к ответам на вопросы и решению типовых задач.

Контрольные вопросы

1. Какие колебания возникают в последовательном колебательном контуре при ступенчатом воздействии, при отключении воздействия, при воздействии прямоугольного импульса?

2. Какие режимы собственных колебаний возможны в последовательном колебательном контуре, и чем они определяются?

3. Какие корни характеристического уравнения соответствуют каждому из этих режимов?

4. Какой физический смысл имеют вещественная и мнимая составляющие комплексно-сопряженных корней характеристического уравнения?

5. Какими соотношениями связаны параметры RLC-контура для каждого режима?

6. Как рассчитать значения С_кр, L_кр, R_кр?

7. Как должны измениться потери в контуре (значение емкости С, индуктивности L), чтобы критический режим перешел в апериодический? колебательный?

8. Может ли частота свободных колебаний ω_св в контуре RLС быть выше (равна, ниже) резонансной частоты ω_о этого же контура?

9. Что понимают под начальными условиями для RLС-контура?

10. Как величина добротности контура влияет на режим собственных колебаний?

11. Как величина добротности влияет на период собственных (свободных) колебаний, декремент затухания и длительность переходного процесса?

Лабораторная работа 3