Решение линейных уравнений по формулам Крамера

Теорема Крамера

Применение формул Крамера к решению систем линейных уравнений

Теорема. Система п уравнений с п неизвестными, определи­тель которой отличен от нуля, всегда имеет решение и притом единственное. Оно находится следующим образом: значение каж­дого из неизвестных равно дроби, знаменателем которой явля­ется определитель системы, а числитель получается из опреде­лителя системы заменой столбца коэффициентов при искомом неизвестном на столбец свободных членов.

Пусть дана система п линейных уравнений с п переменными:

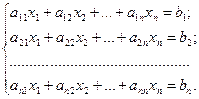
Из коэффициентов при неизвестных составим матрицу А, а из свободных членов — матрицу-столбец В, т. е.

А = 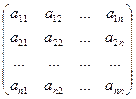, В = .

Определитель матрицы А обозначим ∆ и назовем определителем системы. Таким образом,

.

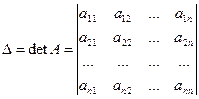Пусть ∆ ≠ 0. Если в определителе системы заменить поочере1дно столбцы коэффициентов при х₁, х₂, ..., х_п на столбец свободных членов, то получим п определителей (для п неизвестных)

, …, .

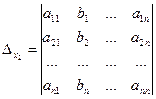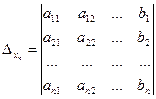Тогда формулы Крамера для решения системы п линейных урав­нений с п неизвестными запишутся так:

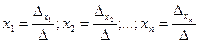
или короче

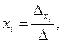где i = 1, 2, …, n.

Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:

1. ∆=0 и каждый определитель ∆_xi=0. Это имеет место
только тогда, когда коэффициенты при неизвестных х_i пропор
циональны, т. е. каждое уравнение системы получается из перво­
го уравнения умножением обеих его частей на число k. Очевидно,
что при этом система имеет бесчисленное множество решений.

2. ∆=0 и хотя бы один из определителей ∆_xi≠0. Это имеет
место только тогда, когда коэффициенты при всех неизвестных,
кроме Xi, пропорциональны. При этом получается система из про­
тиворечивых уравнений, которая не имеет решений.