Следствия из законов Ньютона

Законы механики Ньютона

1) Первый закон Ньютона: Существуют такие системы отсчета, называемые инерциальными, относительно которых свободные тела движется равномерно и прямолинейно.

Первый закон механики, или закон инерции, как его часто называют, бал, по существу, установлен еще Галилеем, но общую формулировку ему дал Ньютон.

Свободным телом – называют тело, на которое не действуют какие – либо другие тела или поля. При решении некоторых задач тело можно считать свободным, если внешние воздействия уравновешены.

Системы отсчета, в которых свободная материальная точка покоится или движется прямолинейно и равномерно, называются инерциальными системами отсчета. Прямолинейное и равномерное движение свободной материальной точки в инерциальной системе отсчета называется движением по инерции. При таком движении вектор скорости материальной точки остается постоянным ( 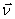= const ). Покой точки является частным случаем движения по инерции ( 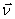=0).

В инерциальных системах отсчета покой или равномерное движение представляет собой естественное состояние, а динамика должна объяснить изменение этого состояния (т.е. появление уско­рения тела под действием сил). Свободных тел, не подверженных воздействию со стороны других тел не существует. Однако, благо­даря убыванию всех: известных взаимодействий с увеличением рас­стояния, такое тело можно реализовать с любой требуемой, точ­ностью.

Системы отсчета, в которых свободное тело не сохраняет ско­рость движения неизменной, называются неинерциальными. Неинерциальной является система отсчета, движущаяся с ускорением отно­сительно любой инерциальной системы отсчета. В неинерциальной системе отсчета даже свободное тело может двигаться с ускорением.

Равномерное и прямолинейное движение системы отсчета не влияет на ход механических явлений, протекающих в ней. Никакие механические опыты не позволяют отличить покой инерциальной системы отсчета от ее равномерного прямолинейного движения. Для любых механических явлений все инициальные системы отсче­та оказываются равноправными. Эти утверждения выражают меха­нический принцип относительности (принцип относительности Галилея). Принцип относительности является одним из наиболее об­щих законов природы, в специальной теории относительности он распространяется на электромагнитные и оптические явления.

Масса, плотность, сила.

Свойство тела сохранять свою скорость при отсутствии взаимодействия с другими телами называется инертностью. Физическая величина, являющаяся мерой инертности тела в поступательном движении, называется инертной массой. Масса тела измеряется в килограммах: 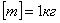. Масса характеризует также способность тела взаимодействовать с другими телами в соответствии с законом всемирного тяготения. В этих случаях масса выступает как мера гравитации и ее называют гравитационной массой.

В современной физике с высокой степенью точности доказана тождественность значений инертной и гравитационной масс данно­го тела. Поэтому говорят просто о массе тела (m ).

В механике Ньютона считается, что

а) масса тела равна сумме масс всех частиц (или материальных точек), из которых оно состоит;

б) для данной совокупности тел выполняется закон сохранения массы: при любых процессах, происходящих в системе тел, ее масса остается неизменной.

Плотность однородного тела равна 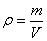. Единица плотности 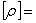1 кг/м³.

Силой называется векторная физическая величина, являющаяся мерой механического воздействия на тело со стороны других тел или полей. Сила полностью определена, если заданы ее модуль, направление и точка приложения. Прямая, вдоль которой направ­лена сила, называется линией действия силы.

В результате действия силы тело изменяет скорость движения (приобретает ускорение) или деформируется. На основании этих опытных фактов производится измерение сил.

Сила является причиной возникновения не скорости, а ускорения тела. С направлением силы совпадает во всех случаях направление ускорения, но не скорости.

В задачах механики учитываются гравитационные силы (силы тяготения) и две разновидности электромагнитных сил - силы упру­гости и силы трения.

Второй закон Ньютона

Второй закон Ньютона описывает движение частицы, вызванное влиянием окружающих тел, и устанавливает связь между ускорением частицы, ее массой и силой, с которой на нее действуют эти тела:

Если на частицу с массой т окружающие тела действуют с силой 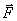, то эта частица приобретает такое ускорение 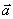, что произведение ее массы на ускорение будет равно действующей силе.

Математически второй закон Ньютона записывается в виде:

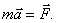
На основе этого закона устанавливается единица силы — 1 Н (нью­тон). 1 Н — это сила, с которой нужно действовать на тело массой 1 кг, чтобы сообщить ему ускорение 1 м/с².

Если сила 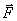, с которой тела действуют на данную частицу, из­вестна, то записанное для этой частицы уравнение второго закона Ньютона называют ее уравнением движения.

Второй закон Ньютона часто называют основным законом дина­мики, так как именно в нем находит наиболее полное математическое выражение принцип причинности и именно он, наконец, позволяет решить основную задачу механики. Для этого нужно выяснить, какие из окружающих частицу тел оказывают на нее существенное действие, и, выразив каждое из этих действий в виде соответствующей силы, следует составить уравнение движения данной частицы. Из уравнения движения (при известной массе) находится ускорение частицы. Зная

же ускорение можно определить ее скорость, а после скорости — и положение данной частицы в любой момент времени.

Практика показывает, что решение основной задачи механики с помощью второго закона Ньютона всегда приводит к правильным результатам. Это и является экспериментальным подтверждением справедливости вто­рого закона Ньютона.

Третий закон Ньютона.

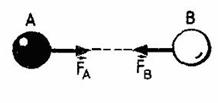
Третий закон Ньютона: Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.

Это означает, что если на тело А со стороны тела В действует сила 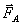, то одновременно на тело В со стороны тела А будет действовать сила 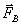, причем = - .

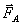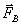Используя второй закон Ньютона, можно записать:

,

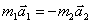Отсюда следует, что

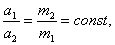
т. е. отношение модулей ускорени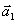й и 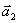взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил. Более массивное тело получает меньшее ускорение, а легкое - большее.

Важно понимать, что силы, о которых идет речь в третьем законе Ньютона, приложены к разным телам и поэтому они не могут уравновешивать друг друга.

Следствия из законов Ньютона

Законы Ньютона представляют собой систему взаимосвязанных законов, которые позволяют глубже понять сущность понятий силы и массы. Следствия из законов:

1. Сила является мерой воздействия, оказываемого на данную частицу со стороны других тел, и с увеличением расстояния до них убывает, стремясь к нулю.

То, что сила является мерой воздействия со стороны окружающих частику тел, следует из того, что она зависит от состояния этих тел и при этом определяет ускорение данной частицы: 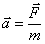. Убывания действующей силы до нуля при неогра­ниченном удалении от частицы окружающих ее тел является следствием первого и второго законов Ньютона. Так как, со­гласно первому закону Ньютона, бесконечно удаленная от всех тел

частица имеет нулевое ускорение 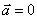. Согласно второму закону Нью­тона 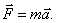Поэтому при 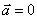и сила .

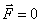2. Сила, с которой сразу несколько тел действует на данную частицу, равна сумме сил, с которыми эти тела действуют на нее по отдельности:

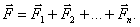
Это утверждение называется принципом независимости взаимодействий. С учетом этого принципа второй закон Ньютона записы­вается в виде:

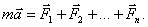
Сумму сил, стоящую в правой части этого закона, называют равнодействующей силой.

Принцип независимости взаимодействий иначе называют принципом суперпозиции сил.

3. Сумма всех внутренних сил, действующих в любой сис­теме, всегда равна нулю.

Под внутренними понимают те силы, которые действуют между телами самой рассматриваемой системы.

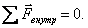
Внутренние силы не способны привести в движение систему тел как целое. Действительно, для этого нужно было бы сообщить ускорение, а ускорение, как это следует из второго закона Ньютона, могут сообщить системе лишь те силы, сумма ко­торых отлична от нуля.

4. Отношение модулей ускорений, полученных двумя те­лами в результате взаимодействия друг с другом, равно обратному отношению их масс:

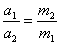
Динамика.

 Динамика рассматривает силы в качестве причины движения тел. При этом следует различать:

• Динамику поступательного движения, или динамику материальной точки, и
• Динамику вращательного движения, или динамику твердого тела.

 Второй закон Ньютона

F₁ + F₂ + F₃ + … = ma,

m − масса тела, F₁ + F₂ + F₃ + … = F − сумма всех сил, действующих на материальную точку.
 Теорема о движении центра масс

М_систa_ц.м. = F_1вн + F_2вн + …,

где М_сист − масса системы материальных точек (масса тела или системы тел), a_ц.м. − ускорение центра масс этой системы, F_1вн + F_2вн + … − сумма внешних сил, действующих на эту систему.

 Третий закон Ньютона

F₁₂ = −F₂₁.

 Сила всемирного тяготения (гравитационная сила)

F = Gm₁m₂/r², [F] = кг•м/c² = H,

G = 6,67 × 10⁻¹¹ H•м²/кг² − гравитационная постоянная, m₁ и m₂ − массы материальных точек, r − расстояние между точками.

 Сила тяжести

F = gm,

g_o = GM/R²,

g = GM/(R + h)² = g_o/(1 + h/R)²,

где g_o − ускорение свободного падения вблизи поверхности планеты, g − ускорение свободного падения на высоте h от поверхности, R − радиус планеты, M − масса планеты. Для планеты Земля R = R_З.

 Первая космическая скорость

v_I = √{gR_З},

 Вторая космическая скорость

v_II = √{2}v_I = √{2gR_З},

R_З − радиус Земли.

 3-й Закон Кеплера

T₁²/T₂² = a₁³/a₂³

где T₁ и T₂ − периоды обращения двух планет вокруг Солнца, а a₁ и a₂ − длины больших полуосей их орбит.

 Вес тела − сила, с которой тело действует на горизонтальную опору или растягивает подвес, находясь в поле тяготения Земли.

 Вес тела в покое или движущегося по вертикали равномерно и прямолинейно

P = mg.

 Вес тела, опускающегося с ускорением или поднимающегося с замедлением

P = m(g − a).

 Вес тела, поднимающегося с ускорением или опускающегося с замедлением

P = m(g + a).

 Перегрузки при подъеме с ускорением или спуске с замедлением

n = P/(mg).

 Сила упругости пружины

F = −kΔx,

k − коэффициент жесткости, [k] = Н/м, Δx = x − x_o, деформация пружины от начальной x_o до конечной x длины.

 Сила упругости стержня, закрепленного на одном конце и свободного на другом

σ = F/S = εE = |Δl|E/l_o = |l − l_o|E/l_o,

E − модуль упругости материала стержня (Юнга), σ − механическое напряжение, ε = |Δl|/l_o − относительное удлинение стержня.

 Сила трения.
Движущееся тело теряет свою энергию, не только преодолевая  сопротивление окружающей среды, на из-за наличия трения. Сила трения действует на поверхности соприкосновения тел и затрудняет их перемещение относительно друг друга.
 Сила трения скольжения

F_тр = μN,

μ − коэффициент трения между телом и поверхностью, зависит от материала поверхностей, шероховатости тела и поверхности, от скорости тела относительно поверхности, N − сила нормального давления, которая прижимает тело к опоре.
Трение покоя проявляется в том случае, когда тело, находившееся в  состоянии покоя, приводится в движение. При отсутствии скольжения, сила трения покоя равна силе, вызывающей движение тела.