Матрицы и действия с матрицами
Матрицей размера 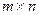 называется прямоугольная таблица чисел, содержащая
называется прямоугольная таблица чисел, содержащая 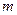 строк и
строк и 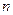 столбцов. Матрицы обозначают прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы[1] и обозначаются строчными буквами с двойным индексом:
столбцов. Матрицы обозначают прописными (заглавными) буквами латинского алфавита. Числа, составляющие матрицу, называются элементами матрицы[1] и обозначаются строчными буквами с двойным индексом: 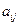 , где первый индекс (
, где первый индекс ( 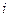 ) соответствует номеру строки, а второй индекс (
) соответствует номеру строки, а второй индекс ( 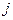 ) – номеру столбца. Матрица размера
) – номеру столбца. Матрица размера 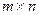 может быть записана в одном из видов
может быть записана в одном из видов
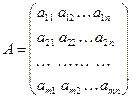
либо 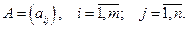
При необходимости указать размер матрицы будем использовать запись 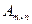 .
.
Элементы матрицы, имеющие одинаковые индексы, называются диагональными. Матрица, у которой ниже главной диагонали стоят нули, называется треугольной.
Матрица, состоящая из одной строки, называется матрицей-строкой, а матрица, состоящая из одного столбца – матрицей-столбцом. Обе такие матрицы называют также вектором.
Матрица, все элементы которой равны нулю, называется нулевой матрицей и обозначается 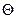 .
.
Если число строк матрицы равно числу столбцов, то матрица называется квадратной, а число строк (столбцов) порядком матрицы.
Квадратная матрица, у которой только диагональные элементы могут быть не равны нулю, называется диагональной матрицей
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается 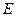 .
.
Матрица, полученная из исходной перестановкой строк со столбцами, называется транспонированной матрицей и обозначается 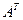 :
:
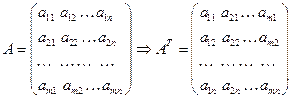 .
.
Заметим, что 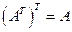 .
.
В математике матрица рассматривается как самостоятельный математический объект, с которым можно производить различные действия.
1. Сравнение матриц. Две матрицы равны, если они имеют одинаковый размер и соответствующие элементы равны:
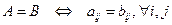 .
.
2. Умножение матрицы на число. Для того чтобы умножить матрицу на число надо умножить на это число все элементы матрицы:
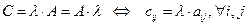 .
.
3. Сложение (вычитание) матриц. Сложение (вычитание) матриц проводится поэлементно и возможно для матриц одного размера:
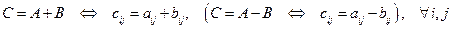 .
.
При сложении и умножении матриц на чило действуют все законы сложения и умножения.
4. Умножение матриц. Матрицы перемножаются по правилу строки на столбец:
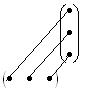
Рис.1
А именно, осуществляется операция, которая называется сумма произведений: элементы, соединенные одной линией перемножаются, а затем результаты складываются. То есть, чтобы получить элемент 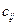 матрицы
матрицы 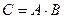 надо каждый элемент
надо каждый элемент 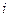 −ой строки матрицы
−ой строки матрицы 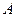 умножить на соответствующий по порядку элемент
умножить на соответствующий по порядку элемент 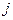 −го столбца и результаты сложить.
−го столбца и результаты сложить.
При записи знак умножения 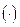 может быть опущен:
может быть опущен: 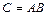 .
.
Умножение матриц возможно только в случае, если число столбцов первой матрицы равно числу строк второй матрицы. Результат умножения – матрица, имеющая число строк, совпадающее с числом строк первой матрицы, и число столбцов равное числу столбцов второй матрицы. При умножении матрицы на вектор-столбец получаем вектор-столбец. При умножении матрицы на транспонированную матрицу получаем квадратную матрицу.
Умножение матриц не коммутативно,т.е. в общем случае 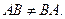 .
.
Роль единицы при умножении матриц играет единичная матрица 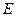 . Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушается порядок множителей и умножение возможно. То есть, верны следующие свойства умножения:
. Для матриц выполнены ассоциативный и дистрибутивный законы умножения, если не нарушается порядок множителей и умножение возможно. То есть, верны следующие свойства умножения:
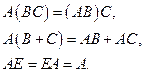
Отметим также свойство умножения для транспонированных матриц
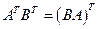 .
.
5. Возведение в степень. Для квадратных матриц определено возведение в натуральную степень, которое проводится как последовательное умножение. При этом, очевидно, справедлив коммутативный закон умножения
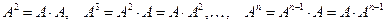 .
.
►Пример 1.
а) Даны матрицы 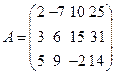 ,
, 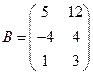
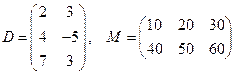 .
.
Выполнить указанные действия:
1) указать размер матрицы  ,
,
2) записать элемент матрицы  ,
,
3) найти: а) транспонированную матрицу 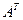 , б) матрицу
, б) матрицу 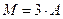 ,
,
4) вычислить 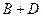 ,
,
5) вычислить 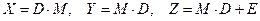 (
( 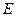 - единичная матрица).
- единичная матрица).
Решение.
1) Матрица 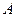 имеет 3 строки и четыре столбца, следовательно, ее размер
имеет 3 строки и четыре столбца, следовательно, ее размер 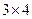 .
.
2) Элемент 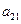 находится во второй строке и первом столбце матрицы
находится во второй строке и первом столбце матрицы 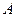 :
: 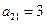 .
.
3) Транспонированная матрица получается из исходной, при замене строк на столбцы, а для записи матрицы 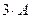 необходимо все элементы матрицы
необходимо все элементы матрицы 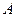 умножить на три:
умножить на три:
а) 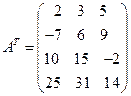 , б)
, б) 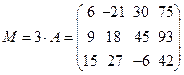 .
.
4) Матрицы 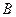 и
и 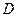 имеют одинаковый размер, следовательно, их можно складывать
имеют одинаковый размер, следовательно, их можно складывать
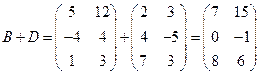 .
.
5) Число столбцов матрицы 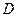 равно числу строк матрицы
равно числу строк матрицы  . Следовательно, возможно умножение
. Следовательно, возможно умножение 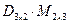 , При этом получаем матрицу
, При этом получаем матрицу 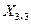 , имеющую три строки и три столбца:
, имеющую три строки и три столбца:
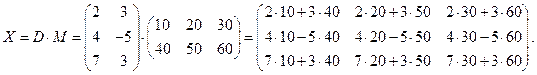
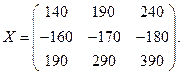
Аналогично возможно и умножение 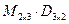 , получаем матрицу
, получаем матрицу 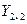 .
.
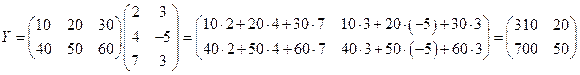 .
.
Так как складывать можно только матрицы одного размера, для нахождения матрицы 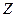 необходимо взять единичную матрицу второго порядка
необходимо взять единичную матрицу второго порядка
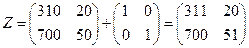 . ◄
. ◄
Упражнения.
1. Даны матрицы: 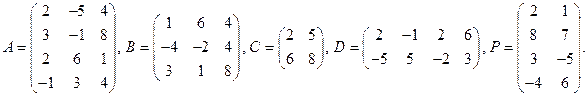
Выполнить действия:
а) 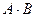 , б)
, б) 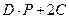 , в)
, в) 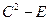 , г)
, г) 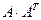 , д)
, д) 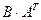 .
.
Ответы:
а) 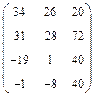 , б)
, б) 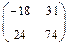 , в)
, в) 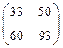 , г)
, г) 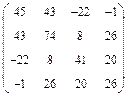 , д)
, д) 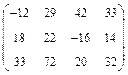 .
.
Определители
Определителем (детерминантом) n-го порядка называется числовая характеристика квадратной матрицы A размера 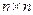 , вычисляемая по определенному правилу (см., например,
, вычисляемая по определенному правилу (см., например,  ). Обозначается определитель одним из символов
). Обозначается определитель одним из символов 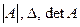 .
.
Определитель первого порядка – определитель для матрицы размера 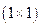 , состоящей из одного числа, – равен самому числу:
, состоящей из одного числа, – равен самому числу:
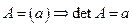 .
.
Для определителей второго и третьего порядков имеем:
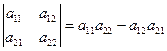 ; (1)
; (1)
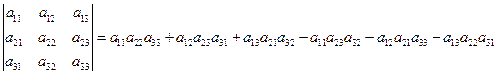 . (2)
. (2)
При вычислении определителя третьего порядка удобно пользоваться следующей схемой (схема Саррюса):
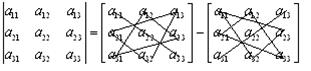
Рис. 2
Определитель равен алгебраической сумме произведений элементов, соединенных на рисунке одной непрерывной линией. Для определителей порядка выше третьего подобных простых схем не составлено, и для вычисления надо использовать упрощения, основанные на свойствах определителей.
Введем несколько важных понятий.
Минором 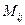 определителя
определителя 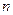 −го порядка называется определитель, полученный из данного вычеркиванием
−го порядка называется определитель, полученный из данного вычеркиванием 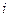 −ой строки и
−ой строки и 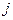 −го столбца.
−го столбца.
Алгебраическим дополнением к элементу 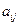 определителя
определителя 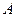 называется выражение
называется выражение
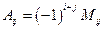 .
.
Для вычисления определителя 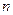 −го порядка справедливы рекуррентные формулы через определители (
−го порядка справедливы рекуррентные формулы через определители ( 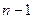 )−го порядка:
)−го порядка:
 (3)
(3)
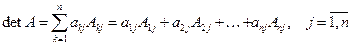 . (4)
. (4)
Свойства определителей.
Так как определитель не меняется при транспонировании матрицы, свойства, приведенные ниже для строк, справедливы и для столбцов.
- Определитель, имеющий нулевую строку равен нулю.
- Определитель, у которого две строки равны или пропорциональны, равен нулю.
- Общий множитель строки можно выносить за знак определителя.
- Перестановка двух строк определителя изменяет знак определителя.
- Если строку определителя умножить на постоянное число и прибавить к другой строке, то определитель не изменится.
- Сумма произведений элементов строки на соответствующие алгебраические дополнения к элементам другой строки равна нулю.
.
- Определитель
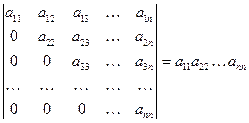 .
.
То есть определитель треугольной матрицы равен произведению ее диагональных элементов.
- Определитель произведения квадратных матриц равен произведению определителей этих матриц:
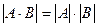 .
.
►Пример 2. Вычислить определители:
1)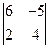 ,2)
,2)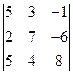 ,3)
,3) 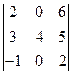 , 4)
, 4) 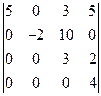 , 5)
, 5) 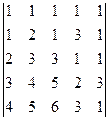 .
.
Решение.
1) Определитель вычислим по формуле (1) 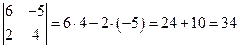 .
.
2) Определитель вычислим по формуле (2) и по формулам (3,4) . По формуле (2)
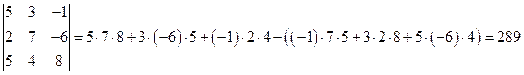 .
.
Для вычисления по формуле (3) возьмем вторую строку (выбор строки произволен) и вычислим миноры и алгебраические дополнения к элементам этой строки
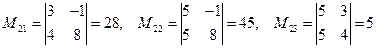 .
.
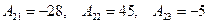 .
.
По формуле (3) имеем 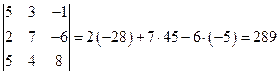 .
.
3) Заметим, что в определителе 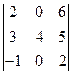 во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец
во втором столбце имеется два нуля. Воспользуемся формулой (4) и выберем для разложения второй столбец
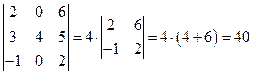 .
.
4) Определитель 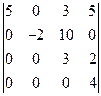 имеет треугольный вид, следовательно,
имеет треугольный вид, следовательно,
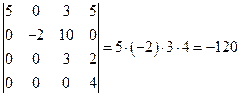 .
.
6) Определитель 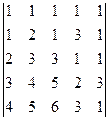 имеет пятый порядок. Разложение по элементам строки (столбца) приводит к четырем определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем
имеет пятый порядок. Разложение по элементам строки (столбца) приводит к четырем определителям четвертого порядка, что в свою очередь дает для каждого из них четыре определителя третьего порядка. Многовато! Воспользуемся пятым свойством определителей. Умножим первую строку на минус единицу и прибавим ее ко второй строке. Затем последовательно первую строку умножим на минус два и прибавим к третьей строке; первую строку умножим на минус три и прибавим к четвертой строке: первую строку умножим на минус четыре и прибавим ее к четвертой строке. Замечаем, что первая строка при наших действиях остается неизменной, поэтому все операции можно сделать за один шаг перехода. Договоримся условно записывать сделанные операции над равенством перехода. Получаем
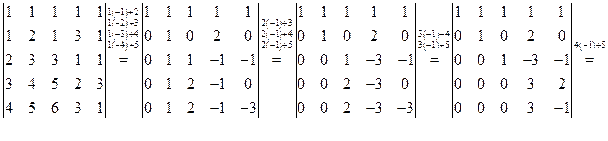
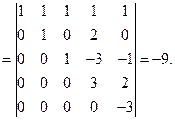
Упражнения.
1. Вычислить определители:
а) 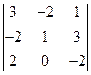 ; б)
; б) 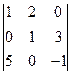 ; в)
; в) 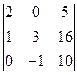 ; г)
; г) 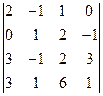 ; д)
; д) 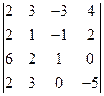 ;
;
е) 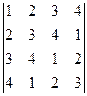 ; ж)
; ж) 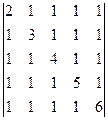 ..
..
Ответы:
а) -12; б) 29; в) 87; г) 0; д) 48; е) 160; ж) 394.
