Исследовать точность отработки системой управления гармонического сигнала

3.1. В блоке Transfer Fcn установить ПФ объекта как в п.2.1.

3.2. В блоке PID Controller задать параметры ПИ-регулятора P=1, I=1, D=0. Подать на вход системы управления сигнал 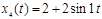. Для этого в блоке Step1 установить значение Final value=2, а в окне настроек блока Sine Wave – параметры гармонического сигнала. Запустить процесс моделирования и измерить постоянную составляющую и амплитуду установившейся гармонической ошибки на графике e(t).

3.3. В ПФ объекта управления добавить в числитель полином

(4s² +5s +1), а в знаменатель – ( 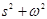), где значение 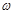взять равным частоте гармонического сигнала .

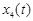В блоке PID Controller установить P=10, I=D=0. Наблюдать процессы x(t), y(t), e(t). Измерить амплитуду y(t) в установившемся режиме и значение установившейся ошибки. Результаты моделирования сохранить.

Исследовать влияние возмущающего воздействия f(t) на точность системы управления.

4.1. Подключить на соответствующие входы системы управления постоянное задающее и возмущающее воздействия: x₁(t)=a₀1(t), f(t)=b₀1(t). Предварительно установить в блоке Step 2 параметр Final Value равным b₀=0,5a₀.

Выбрать в блоке PID Controller П-регулятор, установив Р=10, I=D=0. В блоке Transfer Fcn установить ПФ объекта как в п. 2.3.

4.2.а) Запустить процесс моделирования. По графику e(t) измерить величину установившейся ошибки. Результаты моделирования сохранить.

б) Установив в блоке Step2 b₀=0, запустить процесс моделирования и определить установившуюся ошибку. Результаты моделирования сохранить.

4.3. Исследовать комбинированную систему управления с компенсацией возмущающего воздействия. Для этого:

а) подключить компенсирующее устройство, установив в блоке Gain 1 коэффициент передачи равным единице;

б) задать в блоке PID Controller ПФ ПИ-регулятора

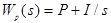, где I=1, а значение P выбирается из таблицы;

в) установить в блоке Transfer Fcn1 ПФ компенсирующего устройства

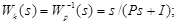
г) отключить задающее воздействие, установив в блоке Step значение Final Value=0;

д) сформировать возмущающее воздействие на объект в виде 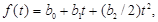где b₀=0,5a₀; b₁=0,5a₁; b₂=0,5a₂.

Для этого установить в блоке Gain единицу, и задать численные значения параметров соответственно в блоках Step2, Ramp и Constant1;

e) подключить на первый вход блока Mux возмущающее воздействие f(t), предварительно удалив линию связи для отображения сигнала x(t);

ж) запустить процесс моделирования и наблюдать сигналы f(t), y(t), e(t). Результаты моделирования сохранить.

Содержание отчета

1. Структурные схемы исследуемых систем.

2. Таблицы и графики зависимостей 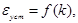полученные в результате моделирования.

3. Графики зависимостей 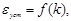полученные расчетным путем.

4. Расчет амплитуды гармонической ошибки по результатам п. 3.2 и сравнение расчетного значения с результатом моделирования.

5. Объяснение отличий результатов, полученных в п. 3.2 и 3.3; в п. 4.2 и 4.3.

6. Результаты выполнения п. 4.3.

Значения параметров	№ варианта
а0	1,5		2,5		3,5
а1, с-1		0,7	0,5	0,4	0,3	0,25
а2 , с-2	0,25	0,3	0,4	0,5	0,6	0,8
Т, с	0,08	0,1	0,15	0,2	0,25	0,3
P

Контрольные вопросы.

1. Определение статической, скоростной ошибок и ошибки по ускорению, понятие статической и астатической системы.

2. Как влияет коэффициент усиления системы на ошибки воспроизведения степенных задающих воздействий?

3. Определить значение установившейся ошибки замкнутой системы с ПФ 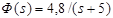при задающем воздействии вида:

а) v(t)=5∙1(t), t≥0; б) v(t)=2sin t, t≥0.

4. Определить коэффициент усиления и порядок астатизма системы управления, если ПФ ошибки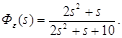

5. Как можно устранить установившуюся ошибку от постоянного возмущающего воздействия?

6.Чем достигается астатизм системы управления (рис.2.1) относительно возмущения?

7. Дать понятие селективной инвариантности системы по отношению к гармоническому воздействию.

Лабораторная работа №4