Методом переменных состояния
Изучите теоретический материал по учебной литературе: [1, с.13; 49–64]; [3, с.196–198] и ответьте на следующие вопросы:
1. Какие переменные в электрической цепи обычно принимают за переменные состояния?
2. Сколько систем уравнений составляют при решении задачи методом переменных состояния?
3. Какие зависимости устанавливаются в первой и во второй системах уравнений при решении задачи методом переменных состояния?
4. Какая из двух систем является системой дифференциальных уравнений, алгебраических?
5. Какие способы используются для получения уравнений состояния и уравнений выходных параметров?
В качестве подготовительных рекомендуется выполнить задачи 8.1 и 8.2. Для аудиторной самостоятельной работы предлагается решение задачи 8.3.
При расчете переходного процесса методом переменных состояния рекомендуется следующий порядок:
1. Выбрать переменные состояния. В предложенных для расчета схемах это напряжения на емкостных элементах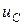 
и токи в индуктивных катушках 
.
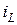2. Составить систему дифференциальных уравнений для первых производных от переменных состояния.
Для этого описать послекоммутационную схему с помощью законов Кирхгофа и решить ее относительно первых производных от переменных состояния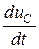 
и 
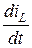в зависимости от переменных , 
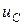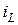и источников э.д.с. (в предлагаемых схемах источник э.д.с. – единственный).
В матричной форме эта система дифференциальных уравнений 1-го порядка будет иметь вид:
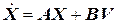, (8.1)
где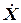 
– столбец производных , ;
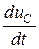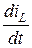Х – вектор - столбец переменных состояния.
В цепях второго порядка:
, 
.
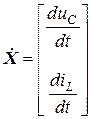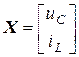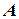– квадратная матрица порядка n, определяемая топологией электрической цепи и параметрами ее элементов. В цепях второго порядка эта матрица имеет порядок 2´2.
Матрица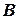 
– прямоугольная матрица порядка 
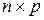, где n – порядок цепи.
Матрица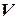 
– столбец 
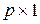– определяется источниками э.д.с. и источниками токов схемы и называется вектором входных величин.
3. Составить систему алгебраических уравнений для искомых переменных, которые называются выходными. Это токи в любых ветвях схемы (кроме тока 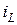) и напряжения на любых элементах схемы (кроме напряжения 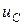). Полученные алгебраические уравнения устанавливают связи между выходными переменными, с одной стороны, и переменными состояния и источниками напряжения и тока схемы – с другой. В матричной форме эта система алгебраических уравнений имеет вид
,
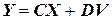где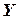 
– вектор выходных величин;
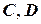– матрицы, определяемые топологией электрической цепи, параметрами ее элементов и количеством искомых переменных.
Для того чтобы описать послекоммутационную схему с помощью законов Кирхгофа и выразить производные 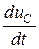и 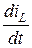через переменные состояния и значения напряжений источников напряжения и токов источников тока, удобно начинать анализ с построения нормального дерева заданной электрической схемы. Нормальное дерево – это дерево, построенное с соблюдением определенного приоритета ветвей, включаемых в его состав, а именно: ветви с источниками напряжения; ветви с емкостными элементами; ветви с резистивными элементами. Заметим, что речь идет о цепях, не содержащих емкостных сечений и индуктивных контуров.