Погрешности компонентов аналитических зависимостей

Тема 4 Таксация древесных стволов и их частей

Определение объема стволовой древесины по аналитическим зависимостям

Погрешности расчетов объема стволовой древесины по аналитическим зависимостям

Погрешности компонентов аналитических зависимостей

Существуют физические (ксилометрический и весовой) и математические способы определения объема древесной массы.

Ксилометрический способ основан на измерении объема воды, вытесненной погруженной в ксилометр древесиной, весовой – на определении массы древесины по массе единицы ее объема.

Математические способы основаны на использовании аналитических моделей образующей древесного ствола или его частей, построенных на основе сходства ее с стереометрическими телами вращения и которые наиболее приемлемы в лесотаксационной практике.

Способы определения объемов древесных стволов и их частей. По диаметрам на разных высотах ствола могут быть найдены площади поперечных сечений древесных стволов по следующей формуле:

g = А + Вх + Сх² + Dx³, где

g - площадь поперечного сечения ствола

с диаметром d, g=0,785 d² • 0,00001;

х - расстояние от шейки корня до рассматриваемого сечения;

А, В, С, D - некоторые постоянные коэффициенты.

Определив площади поперечных сечений стволов, находим объем ствола или его части V. Его рассматривают как сумму бесконечно тонких поперечных отрезков, имеющих вы­соту dx и площадь основания g. Соответственно этому объем равен: 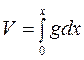. Подставив вместо g его значения, определяемые по кубической параболе, получаем:

.

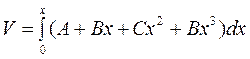Для нахождения коэффициентов А, В, С и D решают урав­нения, определяющие изменение площади поперечных сечений ствола. Размер площадей сечений изменяется в зависимости от расстояния по стволу по формуле:

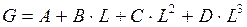
Проведя интегрирование, получают объем древесного ствола в следующем виде: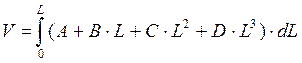

или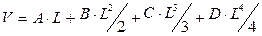

Этот способ наиболее полно учитывает объем ствола. На такой же основе разработаны разнообразные способы определения объема стволов в зависимости от того, сколько сечений ствола (и их площадей) используются для нахождения объема.

Если учитываются значения площади сечения на шейке корня ( 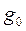) и на любом другом отрезке длины ствола ( 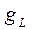), то используя найденные значе­ния коэффициентов и длину ствола L, по­лучаем: .

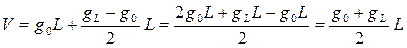Эта формула в лесной таксации называется простой формулой Смалиана.

Если взять вместо полусуммы величин сечений поперечное сечение на половине ствола, тогда формула примет следующий вид: V = γ ·L.

Это соотношение называется фор­мулой определения объема ствола по величине срединного сечения, или формулой объема цилиндра. Впер­вые она была применена немецким лесоводом Губером. В связи с этим ее называют простой формулой Губера.

Если используется значение площади поперечного сечения на 1/3 высоты ствола, а второе - в верхней части, то определение объема ствола проводится по соотношению:.

.

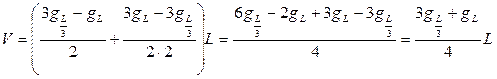Эта формула называется формулой Госфельда.

Для целых стволов (хлыстов), у которых площадь поперечного сечения в верхнем конце равна нулю, формула Госфельда будет иметь та­кой вид:

.

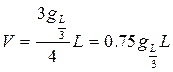При использовании только площади сечения на середине длины (γ), по­лучим: 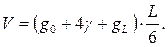Такую фор­мулу первым применил немецкий лесовод Рикке. В связи с этим ее и называют ее простой формулой Ньютона — Рикке.

При использовании приведенных формул для определения объема древесный ствола или его части ствол приравнивают к правильному геометрическому телу - пара­болоиду, поскольку для образующей древесного ствола взято уравнение кубической параболы.

Практически по приведенным соотношениям объем древесных стволов или их частей определяется с некоторой степенью приближения. Поэтому необходимо знать погрешности вычисления объема ствола.

Наиболее точное вычисление объема ствола происходит при расделении его на некоторое количество частей и нахождении объема ствола как суммы объемов этих частей, т.е. .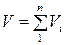

Например, ствол, как правило, делится на отрезки длиной 2 м, если его длина равна 14 и более метров. При меньшей длине ствола отрезки берут длиной 1 или 0,5 м. Необходимо чтобы количество отрезков было не менее 7-10 штук.

Рассмотрим способы определения объема ствола путем деления его длины (L) на «n» равных отрезков длиной ℓна основе рассмотренных выше соотношений.

Площади сечений каждого отрезка обозначим как g₁, g₂ … g_n. Объем каждого отрезка определится как 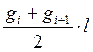. Общий объем будет равен:

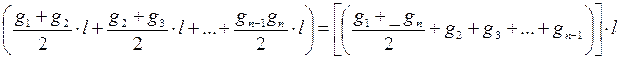Объем вершины определяется как объем конуса, т.е. .

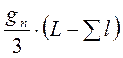Эта формула называется сложной формулой Смалиана.

Наиболее часто в практике научных исследований применяют сложную формулу Губера или срединных сечений.

Обозначив площади сечений середины отрезков через γ имеем:

V = γ₁1 +γ₂l + γ_nl = l (γ₁ + γ₂ + … + γ_n).

При определении объемов отдельных отрезков по сложнойформуле Госфельда, учитывающей сечение на 1/3 длины отрезка и в верхнем отрезке, общий объем ствола будет равен

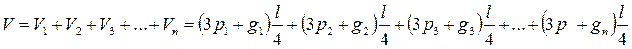В этой формуле сечения на одной трети отрезков 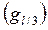обозначены через 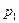, , 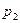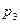и т. д. Преобразовав эту формулу, получим:

.

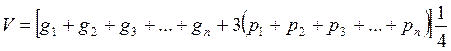При двухметровой длине отрезков при определении объема ствола по формуле Госфельда необходимо измерить диаметры в верхнем сечении каждого отрезка и на 0,67 м от их нижних сечений. В результате преобразований получена следую­щая формула:

.

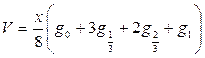При определении объемов отдельных отрезков по сложной формуле Ньютона - Рикке общий объем ствола будет равен

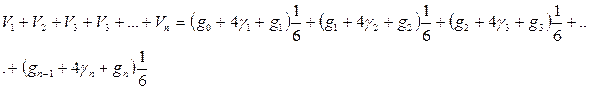
После соответствующих преобразований формула примет такой вид:

,

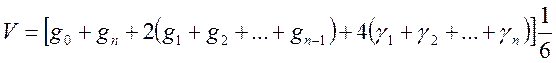где

g – площади сечения на четных разрезах ствола;

γ – площади сечения на нечетных разрезах ствола.

Этот вид уравнения называется формулой Симпсона.

Если ствол разделить на десять отрезков (по методике проф. В. К. Захарова), то объем ствола определяется по соотношению:

,

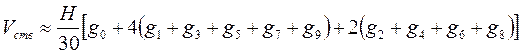где Н – длина ствола,

g₀, g₁, …, g₁₀ – площади сечения на 0,0; 0,1;, …; 1,0 высоты ствола,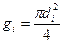

Погрешности расчетов объема стволовой древесины по аналитическим зависимостям. Величины объемов ствола, определяемые ксилометрическим способом, являются наиболее точными. Поэтому принято сравнивать расчетные величины объемов с объемом, найденным ксилометрическим способом, а выявленные расхождения выражать в процентах отклонений

Например, определение объемов дубовых стволов по простой формуле Смалиана дает систематическое преувеличение в среднем на 65%, а по простой формуле Симпсона на 23%. Причиной этого являются корневые наплывы, площадь сечения которых учитывается этими соотношениями (по данным исследований кафедры таксации Воронежского лесохозяйственного института).

Вычисление объемов целых стволов (хлыстов) по простой формуле Губера и Госфельда давало ошибки, как в сторону преуменьшения, так и преувеличения от 8 до 12%.

Американскими исследователями установлено, что определение объема стволов с длиной до 5 м по способу Смалиана систематически завышалось, а по способу Губера – занижалось (ошибка в пределах 10-15%).

Определение же объема более коротких стволов в пределах 1-2м как по формуле Смалиана, так и по формуле Губера давало более низкую ошибку – 6-10%, (США, Янг Г).

Результаты сопоставления вычисленных объемов по сложным форму­лам и найденным ксилометрическим путем, проведенные в Мо­сковской сельскохозяйственной академии им. К. А. Тимиря­зева показывают, что все четыре формулы дают близкие ре­зультаты. Формулы Симпсона и Смалиана дают отклонения с положительным знаком, две другие - с отрицательным.

Объемы, вычисленные по формуле Госфельда и Губера, показывают преуменьшение, что является свойством этих двух формул.

Расхождения в результатах исчисления объемов по всем че­тырем формулам лежат в пределах 2 %.

Отклонения в объемах, вычисленных по сложным формулам

(данные ТСХА им. К. А. Тимиря­зева)

Формула	Отклонение объемов стволов, %
березы 17 шт	сосны 15 шт	дуба 3 шт
Губера	-0,9	-1,2	+1,9
Смалиана	+0,8	-0,3	+0,2
Симпсона	+0,3	-0,2	+0,8
Госфельда	-0,3	-0,6	-0,6

Таким образом, результаты определения объемов по всем четырем формулам следует признать равноценными.

Наиболее часто применяется формула срединного сечения. Она крайне проста, вычисления по ней производить легко, результаты получаются удовлетворительные. В обычных условиях, когда видовое число близко к 0,50, объем большого количества стволов определяется с ошибкой меньшей ±4%, с тенденцией к занижению его значений (-1-2%).

Погрешности измерений компонентов аналитических зависимостей определения объема.

При измерении параметров стволов, участвующих в определении объема деревьев неизбежны ошибки, обусловливающие погрешности последующих расчетов.

Например, ошибка в измерении диаметра влечет за собой равные погреш­ности определения объема и площади сечения;

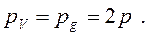
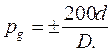, где

d – погрешность определения диаметра;

D – измеряемый диаметр.

Из теории ошибок известно, что относительная ошибка в процентах в объеме стереометрических тел определяется по соотношению:

,

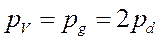а при многочисленных измерениях средняя величина этой ошибки опре­деляется по формуле: .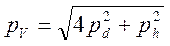

Эти ошибки по свидетельству немецкого профессора М. Продан носят всеобщий характер и возникают в следствии:

· ошибок перечета, так называемых ошибок наблюдения;

· ошибок из-за неправильной формы поперечного сечения стволов;

· ошибок, порождаемых неравно­мерным распределением деревьев в пределах ступеней тол­щины;

· ошибок округления.

Ошибки перечета связаны с дефектами мерной вилки. Они могут быть самой различной величины. Ошибки наблюдения возникают от неправильного положения вилки при перечете и субъективных ошибок (обмера одного дерева 2 раза или его пропуска). При тщательном перечете, по мнению М. Продана, ошибки наблюдения достигают 0,3 % по площади сечения.

Ошибки из-за неправильной формы ствола составляют ±0,5 % по площади сечения.

Ошибки, порождаемые неравномерным распределением деревьев в пределах ступеней толщины, зависят от характера распределения деревьев в данной ступени, со­ставляют – в более мелких ступенях толщины ±0,1- 0,3 %, в бо­лее крупных ±0,03-0,8 % от площади сечения деревьев, вхо­дящих в эту ступень.

Ошибки округления колеблются от - 1,5% до +1 %.