Евклидтік кеңістіктегі беттер

Элементарлық бетті жазықтықтың бөлігін үзіліссіз деформациялау арқылы(созу, қысу және майыстыру) алуға болады. Осылай деформациялау процессі кезінде жазықтықтың нүктесі қайсыбір траекториямен орыyауыстыра отырып беттің нүктесіне өтеді

.

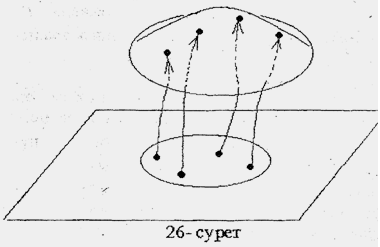
Жалпы жағдайда беттің табиғаты сан алуан болып келеді. Сондықтан оны жазықтықтың бөлігінен деформация арқылы алу мүмкін емес. Олар өзін-өзі қиятын немесе беттескен бөліктері де бар болуы мүмкін. Дегенмен, мұндай беттің әрбір нүктесінің маңайының құрылымы элементарлық бет тәрізді болып келеді.

Беттердің геометриялық қасиеттерін зерттеу үшін оларға кейбір шарттар – регулярлық шартын қоямыз. Ерекшеліктері жоқ беттерді қарастыруымен ғана шектеліп және оларды зерттеу үшін тиімді аппаратты дамытып, біз беттердің кейбір маңызды сипаттамаларын: бірінші және екінші квадраттық формалар, орта және гаусстық қисықтылық және т.б. енгіземіз. Олардың беттердің ішкі және сыртқы геометриялық қасиеттерін суреттеудегі рольдерін көрсетеміз.

Бет туралы ұғым

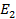евклидтік жазықтықта oij-тік бұрышты координаталар жүйесін берелік.

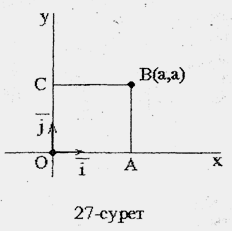Сонда әрбір 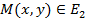нүктеге 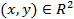нүктесін сәйкес қоятын биективтік 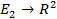бейнелеуі орнатылады. Бұл бейнелеудің гомеоморфизм болатынын байқау қиын емес. Осыны ескерсек, онда біз сандық 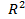кеңістігін 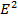жазықтығымен, сандық 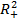- жарты кеңістікті oxy жазықтығының 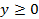болғанда жарты жазықтығымен, ал сандық квадратты OABC квадратымен теңестіре аламыз.(27-сурет)

Анықтама. 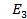кеңістікте өте қарапайым беттер деп келесі фигураларды айтатын боламыз: жазықтықты, тұйық жарты жазықтықты, квадратты.

Өте қарапайым беттердің біріне гомеоморфты фигураны элементарлық бет дейді. Мысалы, эллипстік және гиперболалық параболоидтар, параболалық цилиндр- элементарлық беттер (себебі олардың әрқайсысы жазықтыққа гомеоморфты). Жарты сферада өзінің шекарасымен қоса элементарлық бет болады (дөңгелекке гомеоморфты). Басқаша айтқанда, 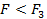фигурасы элементарлық бет болады, егер ол екі өлшемді сандық аралыққа 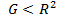гомеоморфты болса.

Анықтама. Саны шектеулі немесе саналымды элементарлық беттер жиынымен бүркеп жабуға болатын 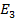кеңістіктегі фигура бет деп аталады.

Анықтамадан, F беттің әрбір M нүктесі үшін 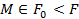шарты орындалатындай 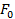элементарлық беті табылатындығы шығады. Элементарлық емес беттерге мысал болатындар: 1) сфера(оны екі жарты сферамен жабуға болады); эллипсоид (ол сфераға гомеоморфты); 2) эллипстік цилиндр(оны саны шектеулі «цилиндрлік жолақтармен» бүркеуге болады, олардың әрқайсысы жазықтыққа гомеоморфты); бір қуысты гиперболоид (ол эллипстік цилиндрге гомеоморфты); 3) қос қуысты гиперболоид (оның әрбір бөлігі жазықтыққа гомеоморфты); 4) гиперболалық цилиндр.

Анықтама.F бетінің M нүктесі үшін кеңістік 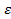–маңайы – 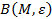табылып, 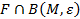қиылысуы элементарлық бет болса, онда М нүктесі кәдімгі нүкте деп аталады. Сонымен қатар, егер бұл қиылысу жазықтыққа гомеоморфты болса, нүкте ішкі деп, ал егер ол тұйық жарты жазықтыққа гомеоморфты болса, онда нүкте шекаралық деп аталады.

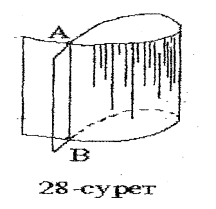
Кәдімгідей емес нүкте ерекше нүкте деп аталады. 28-суретте өзін-өзі АВ түзуінің бойымен қиятын цилиндрлік бет бейнеленген. Бұл түзудің әрбір нүктесі бет үшін ерекше нүкте болады.

Кәдімгі нүктелерден ғана тұратын бетті қарапайым бет деп атайды. Беттің барлық шекаралық нүктелерінің жиыны беттің шекарасы немесе жиегі деп аталады. Әрбір элементарлық бет қарапайым да болады. Сфера, эллипсоид, эллипстік цилиндр, гиперболоидтар қарапайым беттер. Конустық бет қарапайым бет болмайды, себебі оның төбесі ерекше нүкте.

Квадратқа гомеоморфты әрбір беттің жиегі болады және оның жиегі шеңберге гомеоморфты. Ал тұйық жарты жазықтыққа гомеоморфты беттің жиегі түзу сызыққа гомеоморфты. Әрбір қарапайым беттің екіөлшемді көпбейне болатынын(немесе екіөлшемді жиекті көпбейне) байқаймыз.

Бұдан былай біз жазықтыққа(немесе сандық 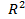кеңістігіне) гомеоморфты жазық облысты G-деп белгілейтін боламыз. Кеңістікте координаталар жүйесін енгізсек, онда 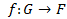гомеоморфизмі G облысын F элементарлық бетіне бейнелейді. Олай болса, f бейнелеуі 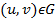нүктесіне 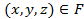нүктесін сәйкес қояды. Яғни G облысында u мен v-дан тәуелді функциялар аламыз:

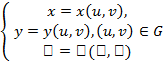(1)

(1)-ші теңдіктер жүйесін Ғ бетінің параметрлік теңдеулері деп атаймыз. Олар мына векторлық функцияға

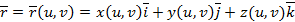(2)

эквивалентті. (2)-ні беттің векторлық теңдеуі дейміз. Келешекте бет (2) векторлық теңдеуімен берілсе, онда 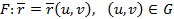деп жазуға келіселік.

(1)-ші функциялар G мен F жиындарының арасында өзара бір мәнді сәйкестік орнатуы үшін

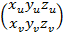(3)

матрицасының G жиынының барлық нүктелеріндегі рангісі екіге тең болуы қажетті және жеткілікті екендігі математикалық анализ курсынан белгілі. (3) матрицада 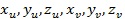деп дербес туындылар белгіленген. Бұл шарттың геометриялық мағынасы мынадай, яғни (3) матрицаның рангісі екіге тең болуы үшін 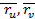векторлары коллинеар болмауы қажетті және жеткілікті,

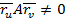(4)

(4) шартты қанағаттандырмайтын нүктелер беттің ерекше нүктелері деп аталады.

Регулярлы беттер. Анықтама. 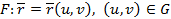беті берілсін. Егер бұл беттің ерекше нүктелері жоқ болса және 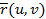векторлық функциясының барлық k-ретті үзіліссіз туындылары бар болса, онда Ғ беті k-ретті регулярлық бет деп аталады және

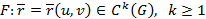
деп жазылады.

Қисықтар теориясындағы сияқты беттердің теңдеулерін де мүмкін өзгертулер арқылы ықшамдауға болады. Мысалы, G және 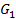облыстарының арасында бір мәнді сәйкестік орнататын 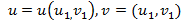функциялар жүйесі берілсін. Егер

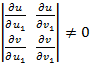
болса және 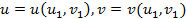функцияларының k-ретті үзіліссіз туындылары бар болса, онда Ғ бетінің векторлық теңдеуін былай жазуға болады:

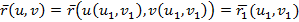
және 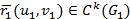. Демек, осы айтылған шарттарды қанағаттандыратындай параметрді өзгерту мүмкіндігі регуляр беттің регулярлық классын өзгертпейді.

Кей ретте беттер 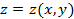түрінде берілуі мүмкін. Мұндай жағдайда бет айқын теңдеумен берілген деп атайды. Оны (1)-ші түрге келтіруге болады. Шындығында, егер 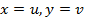деп белгілесек, онда

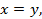
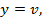
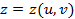
шығады.

Егер бет 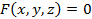, теңдеуімен берілсе, онда бет айқын емес түрде берілген деп атайды. Жалпы, соңғы теңдік бетті анықтау үшін 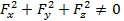болуы керек. Яғни дербес туындылардың бірі нөлден өзгеше болуы қажет. 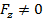болсын. Онда 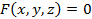теңдігі 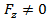қанағаттандырып тұрған нүктенің мейлінше аз маңайында, 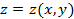функциясын анықтайтыны математикалық анализ курсынан белгілі. Ендеше беттің теңдеуін айқын түрде жазуға болады.