Определение функции двух и более переменных

МАТЕМАТИКА

Методические указания по подготовке

К контрольным работам

Часть 3

Учебно-методическое пособие

Специальности: 080507 Менеджмент организации; 080500 Менеджмент; 080504 Государственное и муниципальное управление; 080505 Управление персоналом

ЧЕРЕПОВЕЦ

2012

Рассмотрено на заседании кафедры математики, протокол № 3 от 20.10.11 г.

Одобрено редакционно-издательской комиссией ФОМ и ЕНД ФГБОУ ВПО ЧГУ, протокол № 1 от 25.10.11 г.

Составитель: Г.А. Киселева

Рецензенты: Н.О. Сорокина, канд. физ.-мат. наук, доцент (ЧГУ);

О.А. Кашинцева, канд. тех. наук,доцент (ЧГУ)

Научный редактор: Н.В. Плотникова, канд. физ.-мат. наук, доцент

© Киселева Г.А., 2012

© ФГБОУ ВПО «Череповецкий государственный университет», 2012

Введение

Данное учебно-методическое пособие предназначено для студентов экономических специальностей дневной и заочной форм обучения.

Пособие содержит решения примерных вариантов контрольных работ и краткие теоретические сведения по темам «Дифференциальное исчисление функций нескольких переменных», «Дифференциальные уравнения».

Задания в контрольных работах составлены с учетом требований Государственного стандарта по специальностям: 080507 «Менеджмент организации», 080500 «Менеджмент», 080504 «Государственное муниципальное управление», 080505 «Управление персоналом».

Пособие поможет студентам самостоятельно подготовиться к контрольным работам, восполнить обнаруженные пробелы в знаниях.

Контрольная работа 3.1

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Краткие теоретические сведения

Определение функции двух и более переменных

Если каждой паре (x; y) значений двух независимых переменных из области D соответствует по некоторому правилу f единственное значение z из Z, то говорят, что z = f(x; y) – функция двух переменных x и y.

Совокупность пар (x; y), при которых определена функция
z = f(x; y), называют областью определения функции двух переменных.

Если каждую пару (x; y) изображать точкой на плоскости, то область определения – совокупность точек на плоскости (или вся плоскость).

Примеры.

1) 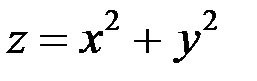. Область определения – вся плоскость.

2)

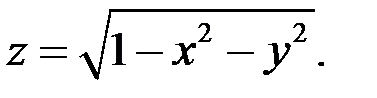
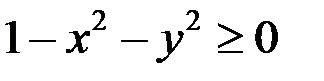или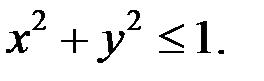

Область определения – круг с центром в начале координат и радиусом равным 1.

Если каждой совокупности (x₁; x₂; …; x_n) значений
n-независимых переменных из пространства Rⁿ соответствует по некоторому правилу f единственное значение z из Z, то говорят, что
z = f(x₁; x₂; …; x_n) – функция n – независимых переменных.

Способы задания функции нескольких переменных те же, что и для функции одной переменной. Наиболее распространенный – аналитический.

Геометрическое изображение

Функция одной переменной изображается на плоскости в виде линии y = f(x).

Функция двух переменных изображается в пространстве в виде поверхности, которая определяется уравнением z = f(x; y).

Примеры.

1) z – 2x + 5y + 10 = 0 – уравнение плоскости. Данная плоскость – график функции z = 2x – 5y – 10.

2) x² + y² + z² = R² – уравнение сферы , радиуса R , с центром в начале координат. С другой стороны, сфера есть объединение графиков двух функци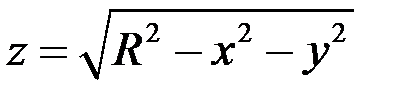й и .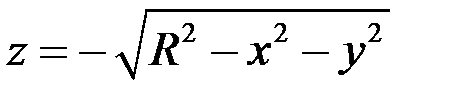

График функции двух переменных – геометрическое место точек (x; y; f(x; y)).

Построение графиков функций двух переменных во многих случаях представляет значительные трудности. Поэтому существует ещё способ изображения функции двух переменных, основанный на сечении поверхности z = f(x; y)плоскостями z = C, где C – любое число, то есть плоскостями, параллельными OXY.

Множество точек, в которых функция z = f(x; y), принимает одно и то же значение C, называют линией уровня функции. C – уровень.

Если взять числа c₁, c₂, …, c_n, образующие арифметическую прогрессию с разностью h, то получим ряд линий уровня, по взаимному расположению которых можем получить представление о графике функции, то есть о форме поверхности. Там, где линии располагаются «гуще», функция изменяется быстрее (поверхность идет круче), а в тех местах, где линии уровня располагаются реже, функция изменяется медленнее (поверхность более пологая). Чем меньше h, тем точнее представление о графике функции.

Пример.

у

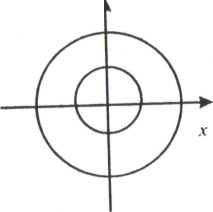Построить линии уровня функции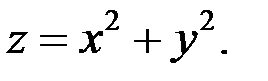

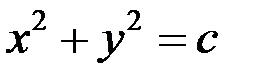(0 ≤ с < +∞).

Придавая с различные значения, получим семейство линий уровня, представляющих собой концентрические окружности.

При с = 0 окружность вырождается в точку (0; 0). Так как в данном случае линии уровня – окружности с центром в начале координат, то графиком функции должна быть поверхность вращения вокруг оси OZ. Из аналитической геометрии известно, что уравнение 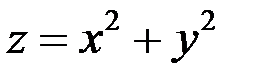определяет параболоид вращения.

Замечание. Функцию трех или более переменных изобразить с помощью графика в пространстве невозможно.