Указания к выполнению контрольных заданий 3 страница
Расчеты проведем в рабочей таблице.
| t | 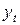 | 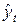 |  |  | |
| 1994 | -2,5 | 30 | 30,0476 | -0,0476 | 0,0023 |
| 1995 | -1,5 | 35 | 34,7619 | 0,2381 | 0,0567 |
| 1996 | -0,5 | 39 | 39,4762 | -0,4762 | 0,2268 |
| 1997 | 0,5 | 44 | 44,1905 | -0,1905 | 0,0363 |
| 1998 | 1,5 | 50 | 48,9048 | 1,0952 | 1,1995 |
| 1999 | 2,5 | 53 | 53,6190 | -0,6190 | 0,3832 |
| Суммы | 0,00 | 251 | 197,3810 | 0,0000 | 1,9048 |

Табличное значение t - критерия Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = 6 – 2 = 4 составляет 2,78, т.е.  =2,78.
=2,78.
Отсюда,

Таким образом,
 ;
;
 .
.
С вероятностью 0,95 можно ожидать, что в 2000 году расходы семьи на товар "А" будут находиться в пределах от 55,4089 до 61,2577 руб.
Обратите внимание на то, что приведенные формулы верны только для уравнения парной регрессии, линейной по параметрам.
Задача 4 посвящена теме «Временные ряды в эконометрических исследованиях».
Рассмотрим методику решения задачи на примере:
Имеются следующие данные о величине дохода в расчете на одного члена семьи в процентах к 1994 году и о расходах семьи на товар "А" в 1994-1999 гг.:
| Годы | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Расходы на товар "А", руб. | 30 | 35 | 39 | 44 | 50 | 53 |
| Доход на одного члена семьи в процентах к 1994 году, % | 100 | 103 | 105 | 109 | 115 | 118 |
Пункт 1. Определение функциональной формы трендового уравнения регрессии описано в пункте 2 к задаче 3.
Пункты 2-3. При измерении корреляции между двумя временными рядами следует учитывать возможность наличия ложной корреляции, обусловленной простым сопутствием временных рядов. Для того чтобы устранить ложную корреляцию, следует определять степень тесноты связи не самих уровней временных рядов, а их последовательных (первых или вторых) разностей или отклонений от трендов (если последние не содержат тенденции).
Сделайте вывод о наличии или отсутствии ложной корреляции при разных способах измерения связи между исследуемыми временными рядами, поясните причины существования ложной корреляции.
По данным примера рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по исходным уровням ряда:

Заметим, что расчет может быть осуществлен и по другим формулам.
Промежуточные расчеты проведем в рабочей таблице.
| Годы | y | x | xy | y2 | x2 |
| 1994 | 30 | 100 | 3000 | 900 | 10000 |
| 1995 | 35 | 103 | 3605 | 1225 | 10609 |
| 1996 | 39 | 105 | 4095 | 1521 | 11025 |
| 1997 | 44 | 109 | 4796 | 1936 | 11881 |
| 1998 | 50 | 115 | 5750 | 2500 | 13225 |
| 1999 | 53 | 118 | 6254 | 2809 | 13924 |
| Суммы | 251 | 650 | 27500 | 10891 | 70664 |

Близкое к единице значение коэффициента корреляции свидетельствует о тесной прямой связи между расходами на товар "А" и доходом на одного члена семьи.
Однако, учитывая, что расчет был произведен по уровням временного ряда, корреляция между изучаемыми признаками может быть вызвана простым сопутствием явлений во времени.
Для того, чтобы исключить тенденцию, рассчитаем коэффициент корреляции по первым разностям.
Промежуточные расчеты проведем в рабочей таблице.
| Годы | y | x | Δy | Δx | ΔxΔy | Δy2 | Δx2 |
| 1994 | 30 | 100 | |||||
| 1995 | 35 | 103 | 5 | 3 | 15 | 25 | 9 |
| 1996 | 39 | 105 | 4 | 2 | 8 | 16 | 4 |
| 1997 | 44 | 109 | 5 | 4 | 20 | 25 | 16 |
| 1998 | 50 | 115 | 6 | 6 | 36 | 36 | 36 |
| 1999 | 53 | 118 | 3 | 3 | 9 | 9 | 9 |
| Суммы | 251 | 650 | 23 | 18 | 88 | 111 | 74 |
 .
.
 .
.
Коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи, рассчитанный по первым разностям, показывает не столь тесную связь, как коэффициент, рассчитанный по уровням ряда динамики.
Расчет коэффициента корреляции по первым разностям позволяет устранить тенденцию, зависимость между x и y, обусловленную сопутствием рядов во времени.
Рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по отклонениям от тренда.
Прежде, чем рассчитывать отклонения от тренда, определим функциональную форму трендовых уравнений регрессии расходов на товар "А" и дохода на одного члена семьи.
Слабая колеблемость первых разностей (цепных абсолютных приростов) позволяет говорить о линейной форме обеих моделей.
Трендовое линейное уравнение регрессии расходов на товар "А" имеет вид (расчеты см. в методических указаниях к решению задачи 3):
 .
.
Аналогично рассчитаем параметры трендового линейного уравнения регрессии доходов в расчете на одного члена семьи:
| Годы | t | x | xt | t2 |
| 1994 | -2,50 | 100 | -250 | 6,25 |
| 1995 | -1,5 | 103 | -154,5 | 2,25 |
| 1996 | -0,5 | 105 | -52,5 | 0,25 |
| 1997 | 0,5 | 109 | 54,5 | 0,25 |
| 1998 | 1,5 | 115 | 172,5 | 2,25 |
| 1999 | 2,5 | 118 | 295 | 6,25 |
| Суммы | 0 | 650 | 65 | 17,5 |

Таким образом, трендовое линейное уравнение регрессии имеет вид:
 .
.
Перейдем к расчету коэффициента корреляции по отклонению от тренда согласно формуле:

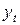 | 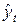 |  |  |  |  |  |  |   | |
| 1994 | 30 | 30,0476 | -0,0476 | 0,0023 | 100 | 99,0476 | 0,9524 | 0,9070 | -0,04535 |
| 1995 | 35 | 34,7619 | 0,2381 | 0,0567 | 103 | 102,7619 | 0,2381 | 0,0567 | 0,056689 |
| 1996 | 39 | 39,4762 | -0,4762 | 0,2268 | 105 | 106,4762 | -1,4762 | 2,1791 | 0,702948 |
| 1997 | 44 | 44,1905 | -0,1905 | 0,0363 | 109 | 110,1905 | -1,1905 | 1,4172 | 0,226757 |
| 1998 | 50 | 48,9048 | 1,0952 | 1,1995 | 115 | 113,9048 | 1,0952 | 1,1995 | 1,199546 |
| 1999 | 53 | 53,6190 | -0,6190 | 0,3832 | 118 | 117,6190 | 0,3810 | 0,1451 | -0,23583 |
| Суммы | 251 | 197,3810 | 0,0000 | 1,9048 | 650 | 532,3810 | 0,0000 | 5,90476 | 1,90476 |
 .
.
Величина этого коэффициента корреляции еще более убедительно свидетельствует о сопутствии рядов во времени.
Пункт 4. По аналогии с коэффициентами корреляции параметры уравнения регрессии по временным рядам определяют также не по исходным их уровням, а по последовательным разностям, либо отклонениям от тренда.
Обратите внимание на интерпретацию параметров, полученных уравнений регрессии:
- если уравнение регрессии построено по первым разностям, то коэффициент регрессии b характеризует изменение прироста результативного признака при изменении прироста факторного признака на единицу.
Сделайте общий вывод о наличии и тесноте причинно-следственной связи между изучаемыми временными рядами, укажите ее направление.
Определим параметры уравнения парной линейной регрессии по первым разностям.
Расчет осуществляется обычным методом наименьших квадратов:
| Годы | y | x | Δy | Δx | ΔxΔy | Δy2 | Δx2 |
| 1994 | 30 | 100 | |||||
| 1995 | 35 | 103 | 5 | 3 | 15 | 25 | 9 |
| 1996 | 39 | 105 | 4 | 2 | 8 | 16 | 4 |
| 1997 | 44 | 109 | 5 | 4 | 20 | 25 | 16 |
| 1998 | 50 | 115 | 6 | 6 | 36 | 36 | 36 |
| 1999 | 53 | 118 | 3 | 3 | 9 | 9 | 9 |
| Суммы | 251 | 650 | 23 | 18 | 88 | 111 | 74 |

Отсюда, модель имеет вид:

Коэффициент регрессии b = 0,5652 означает, что с изменением прироста душевого дохода на 1 процентный пункт расходы на товар "А" изменяются с ускорением, равным 0,5652 руб.
Контрольные задания
Задача 1
Задания:
1) Постройте поле корреляции результативного и факторного признаков.
2) Определите параметры уравнения парной линейной регрессии. Дайте интер претацию найденных параметров и всего уравнения в целом.
3)Постройте теоретическую линию регрессии, совместив ее с полем корреляции. Сделайте выводы.
4)Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
5)С вероятностью 0,95 оцените статистическую значимость коэффициента регрессии и уравнения регрессии в целом. Сделайте выводы.
6) С вероятностью 0,95 постройте доверительный интервал для прогноза оценки  и доверительный интервал генерального значения
и доверительный интервал генерального значения  (
(  -задается отдельно в условии каждой задачи).
-задается отдельно в условии каждой задачи).
7)Определите значение коэффициента эластичности и объясните его.
1.Туристическая компания предлагает места в гостиницах приморского курорта. Менеджера компании интересует, насколько возрастает привлекательность гостиницы в зависимости от ее удаленности от пляжа. С этой целью по 14 гостиницам города была выяснена среднегодовая наполняемость номеров и расстояние от пляжа:
| Расстояние, км | 0,1 | 0,1 | 0,2 | 0,3 | 0,4 | 0,4 | 0,5 | 0,6 | 0,7 | 0,7 | 0,8 | 0,8 | 0,9 | 0,9 |
| Наполняемость, % |
К пункту 6. Значение  =0,65.
=0,65.
2.Компанию по прокату автомобилей интересует зависимость между пробегом автомобилей и стоимостью ежемесячного обслуживания. Для выяснения характера этой связи было отобрано 15 автомобилей. Результаты исследования представлены в таблице:
| Пробег, тыс. км | |||||||||||||||
| Стоимость обслуживания, у.е. |
К пункту 6. Значение  =18,5.
=18,5.
3.Торговцу нужно выяснить, как изменяется количество пучков салата, продаваемых ежедневно в розницу. Имеются следующие сведения о количестве и цене:
| Количество, тыс./день | ||||||||
| Цена, у.е. за единицу |
К пункту 6. Значение  =20.
=20.
4.Компания, занимающаяся продажей радиоаппаратуры, установила на видеомагнитофон определенной модели цену, дифференцированную по регионам. Следующие данные показывают цены на видеомагнитофон в 8 различных регионах и соответствующее им число продаж:
| Число продаж, шт. | ||||||||
| Цена, у.е. | 5,5 | 6,0 | 6,5 | 6,0 | 5,0 | 5,6 | 4,5 | 5,0 |
К пункту 6. Значение  =5,75.
=5,75.
5.Некоторая компания недавно провела рекламную кампанию в магазинах с демонстрацией антисептических качеств своего нового моющего средства. Через 10 недель компания решила проанализировать эффективность этого вида рекламы, сопоставив еженедельные объемы продаж с расходами на рекламу (тыс. руб.):
| Объем продаж, у.е. | ||||||||||
| Расходы на рекламу, у.е. |
К пункту 6. Значение  =7,5.
=7,5.
6. По 10 однородным предприятиям имеются данные о количестве рабочих с профессиональной подготовкой и количестве бракованной продукции:
| № предприятия | ||||||||||
| Количество рабочих с профессиональной подготовкой, % | ||||||||||
| Количество бракованной продукции, % |
К пункту 6. Значение  =27.
=27.
7.При исследовании годового дохода и сбережений населения в случайном порядке отобрано 9 человек. Получены следующие данные:
| Доход, тыс. у.е. | |||||||||
| Сбережения, у.е.. |
К пункту 6. Значение  =17.
=17.
8.Проведен опрос случайно выбранных 10 студентов, проживающих в общежитии университета, для выявления зависимости между средним баллом по результатам предыдущей сессии и числом часов в неделю, затраченных студентом на самостоятельную подготовку:
| Средний балл | 4,6 | 4,3 | 3,8 | 3,8 | 4,2 | 4,3 | 3,8 | 4,0 | 3,1 | 3,9 |
| Число часов |
К пункту 6. Значение  =27.
=27.
9. Имеются данные по 14 предприятиям о производительности труда и коэффициенте механизации работ:
| Коэффициент механизации работ, % | ||||||||||||||
| Производительность труда, шт. |
К пункту 6. Значение  =65.
=65.
10. Представлены данные, характеризующие зависимость между количеством внесенных удобрений и урожайностью картофеля:
| Удобрения, кг/га. | Картофель, ц/га. |
К пункту 6. Значение  =160.
=160.
Задача 2
Задания:
1) Определите парные и частные коэффициенты корреляции, корреляции, проверьте их значимость для α = 0,05, сделайте выводы.
2) Постройте линейное уравнение множественной регрессии, поясните экономический смысл его параметров и всего уравнения в целом. Проверьте значимость параметров уравнения регрессии на уровне значимости α = 0,05.
3) Рассчитайте коэффициенты эластичности. Дайте их интерпретацию.
4) Найдите множественный коэффициент корреляции и детерминации, объясните их смысл.
5)Проверьте наличие мультиколлинеарности в модели, вычислив значение показателя VIF.
6) Проверьте значимость полученного уравнения регрессии в целом на уровне значимости α = 0,05.Сделайте выводы.
1. В конце семестра студенты сдают экзамены. Перед сдачей экзаменов в 20 группах был проведен опрос о том, какую оценку по сдаваемым в сессию курсам они ожидают получить. После сессии полученные оценки были сопоставлены с ожидаемыми оценками и числом студентов в группах.
| Средняя оценка по предмету в i-той группе студентов | Ожидаемая оценка | Число студентов в группе |
| 4,1 3,4 3,3 3,0 4,7 4,6 3,0 4,6 4,6 3,6 3,5 4,0 3,6 3,1 3,3 4,5 2,8 3,7 3,8 3,9 | 3,4 3,1 3,0 2,8 3,7 3,5 2,9 3,7 3,5 3,2 3,0 3,5 3,3 3,1 3,3 3,9 2,9 3,2 3,4 3,4 |
2. Имеются следующие данные о результатах аукционных торгов старинными часами:
| № п/п | Цена продажи, тыс. у.е. | Возраст часов, лет | Число участников аукционных торгов, чел. | № п/п | Цена продажи, тыс. у.е. | Возраст часов, лет | Число участников аукционных торгов, чел. |
| 1,2 | 1,7 | ||||||
| 1,1 | 1,0 | ||||||
| 0,8 | 1,1 | ||||||
| 1,5 | 1,1 | ||||||
| 1,0 | 1,2 | ||||||
| 2,0 | 1,3 | ||||||
| 1,8 | 1,5 | ||||||
| 1,2 | 0,9 | ||||||
| 1,3 | 1,1 | ||||||
| 0,9 | 1,2 |
