Лекция 5. «Элементы математической статистики»

Математическая статистика − раздел математики, изучающий математические методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей.

Теория вероятностей позволяет выражать вероятности сложных событий через вероятности элементарных событий, а математическая статистика по результатам наблюдений (по выборке) позволяет оценить вероятности случайных событий или осуществить проверку гипотез о значении этой вероятности.

Опр.1. Генеральной совокупностью называют совокупность объектов, подлежащих изучению с точки зрения некоторого количественного признака. Количество таких объектов называют объемом генеральной совокупности.

Опр.2. Выборочной совокупностью или выборкой называется совокупность случайно отобранных из генеральной совокупности объектов. Количество таких объектов называют объемом выборки.

Опр.3. Выборку называют повторной, если отобранный объект (перед отбором следующего) возвращают в генеральную совокупность. В противном случае выборку называют бесповторной.

Для обеспечения репрезентативности выборки, применяют различные способы отбора объектов: 1) простой (из генеральной совокупности извлекают по одному объекту); 2) типический (генеральную совокупность делят на части, например, по возрасту, полу, социальному положению, профессии и осуществляют простой отбор из каждой части); 3) механический (отбор производится через определенный интервал,например, вопросы анкеты задаются только каждому 10 участнику); 4) серийный (объекты из генеральной совокупности извлекаются группами (сериями) и обследуются полностью).

Опр.4. Ряд числовых значений называют ранжированным, если все значения располагаются в порядке неубывания.

Опр.5. Значения 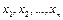, кот. принимает СВ 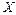в результате эксперимента, называют вариантами этой случайной величины.

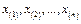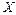Опр.6. Последовательность значений СВ , полученная в результате ранжирования, наз-ся вариационным рядом.

Опр.7. Числа 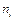, показывающие сколько раз встречаются (повторяются) варианты 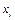в вар. ряду, наз-ся частотами. 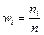− относительные частоты или частости, где .

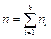Опр.8. Список вариантов и их частот наз-ся статистическим распределением выборки или статистическим рядом. Статистическое распределение выборки яв-ся оценкой (приближением) неизвестного закона распределения вероятностей и записывается в виде таблицы, в которой первая строка содержит варианты СВ, а вторая строка − их частоты. Если же СВ непрерывная или дискретная с большим количеством вариант, то составляют интервальный статистический ряд. 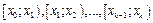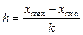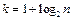В первую строку записывают частичные промежутки , которые обычно берут одинаковой длины , где − количество интервалов. За начало первого интервала берут 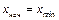, а 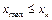(необходимо 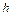всегда округлять с избытком). Во вторую строку записывают частоты или относительные частоты попадания вариант в данный част. промежуток.

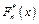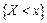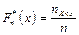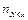Опр.9. Эмпирической функцией распределения называется функция , кот. каждому событию ставит в соответствие его относит. частоту , где − количество значений СВ 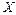, удовлетворяющих неравенству .

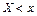Опр.10. Полигоном частот называют ломаную, отрезки которой соединяют точки с координатами 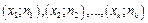в дискретном случае и точки 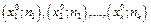в непрерывном случае, где 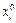− середина част. промежутка .

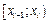Опр.11. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные промежутки длины 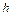, а высоты равны отношению частоты и длины частичного промежутка 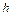, т.е. 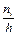− плотность частоты. Аналогично последним понятиям определяются понятия полигона, гистограммы относительных частот.

Вычисление числовых характеристик выборки аналогично вычислению числовых характеристик СВ в теории вероятностей.

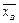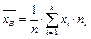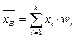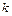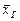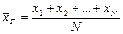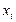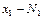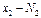Опр. 12. Выборочным средним называется среднее арифметическое всех значений выборки: или , где − количество различных вариант (количество частичных промежутков). Генеральной средней называется среднее арифметическое возможного значения Если различные значения признака Х принимаются раз, раз, … , 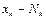раз, тогда 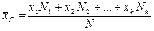. Генеральная средняя есть математическое ожидание рассматриваемого признака Х.

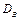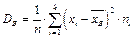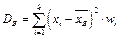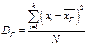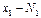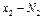Опр.13. Выборочной дисперсией наз-ся: или .Генеральная дперсия . Если раз, раз, … , 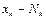раз, то .

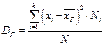Опр.14.Выб-м средним квадратическим отклонением наз-ся 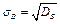. Средним квад. отклонением ген. сов-ти наз-ся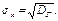

Опр.15. Исправленной выборочной дисперсией называется величина 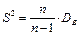. 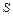− исправленное среднее квадратическое отклонение. При большом объеме выборк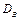и и 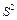мало отличаются. Исправленную дисперсию применяют для выборок малого объема ( 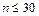). Исправленная дисперсия в отличие от выборочной является несмещенной оценкой ген. дисперсии.

Опр.16. Модой 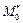вариационного ряда называется варианта, имеющая наибольшую частоту.

Опр.17. Медианой 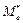вариационного ряда называется значение количественного признака, приходящееся на середину ряда.

Опр.18. Центральным моментом 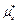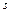-го порядка вариационного ряда называется величина .

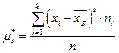Опр.19. Асимметрия вар. ряда 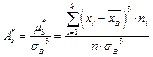. Опр.20. Эксцесс вар. ряда .

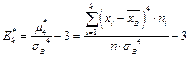Зам. Отрицательная асимметрия означает, что кривая плотности распределения, построенная по эмпирическим данным, является более пологой слева. Положительная асимметрия означает, что такая кривая более пологая справа. Эксцесс позволяет сравнить данную кривую с кривой нормального распределения, для которой он равен 3. Если эксцесс (показатель островершинности) положителен, то данная кривая будет выше кривой нормального распределения, а в противном случае, ниже.

ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ

Опр.21. Статистической оценкой 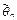параметра 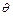теоретического распределения (т.е. распределения количественного признака генеральной совокупности) называют его приближенное значение, зависящее от выборки.

Опр.22. Если 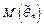= 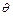, то оценка 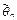называется несмещенной. В противном случае − смещенной.

Опр.23. Оценка 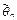пар-ра 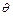наз-ся состоятельной, если она сх-ся по вер-ти к оцен. параметру ( .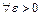

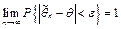Опр.24. Несмещ. оценка 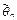пар-ра 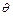наз-ся эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра .

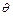Рассмотрим точечные оценки (т.е. оценки, которые характеризуют искомый параметр одним числом) математического ожидания и дисперсии, т.е. эти оценки будем вычислять по выборке.

Т.1. Если 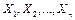− выборка из генеральной совокупности и 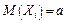, , 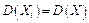то выборочное среднее 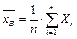− несмещенная и состоятельная оценка математического ожидания 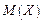, а исправленная выборочная дисперсия 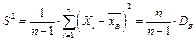− несмещенная и состоятельная оценка дисперсии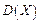

Зам. В случае, когда объем выборки невелик, точечные оценки приводят к ошибкам, т.к. дают большую погрешность. Этого недостатка лишены интервальные оценки неизвестного параметра 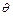, т.е. те, которые определяются концами интервала.

Опр.25. Интервал 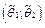, покрывающий с вероятностью 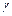истинное значение параметра 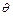, наз-ся доверительным интервалом, а число 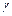− надежностью оценки или доверительной вероятностью. Доверительный интервал выбирают симметричным относительно несмещенной точечной оценки параметра 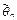, т.е. 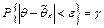, где число 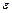характеризует точность оценки.

Рассмотрим интервальные оценки для параметров нормального распределения, т.е. для математического ожидания.

Используем формулу вероятности попадания в интервал в случае нормального распределения, для СВ 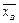имеем: 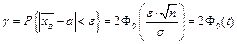, где 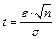. Поскольку 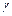было задано, то по таблице значений функции Лапласа из равенства 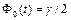находим аргумент t. Находим 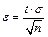(из этой формулы следует, что с возрастанием объема выборки точность оценки увеличивается, а увеличение надежности уменьшает точность оценки), следовательно 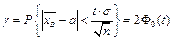. Таким образом, интервал 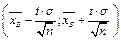- доверительный интервал для .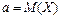