Теорема о движении центра масс
В ряде случаев для определения характера движения системы (особенно твердого тела), достаточно знать закон движения ее центра масс. Например, если бросить камень в цель, совсем не нужно знать как он будет кувыркаться во время полета, важно установить попадет он в цель или нет. Для этого достаточно рассмотреть движение какой-нибудь точки этого тела.
Чтобы найти этот закон, обратимся к уравнениям движения системы и сложим почленно их левые и правые части. Тогда получим:
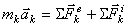 .
.
Преобразуем левую часть равенства. Из формулы для радиус-вектора центра масс имеем:
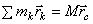 .
.
Беря от обеих частей этого равенства вторую производную по времени и замечая, что производная от суммы равна сумме производных, найдем:
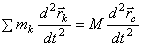
или
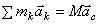 .
.
где 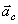 - ускорение центра масс системы. Так как по свойству внутренних сил системы
- ускорение центра масс системы. Так как по свойству внутренних сил системы 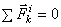 , то, подставляя все найденные значения, получим окончательно:
, то, подставляя все найденные значения, получим окончательно:
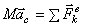 (4)
(4)
Уравнение и выражает теорему о движении центра масс системы: произведение массы системы на ускорение ее центра масс равно геометрической сумме всех действующих на систему внешних сил. Сравнивая с уравнением движения материальной точки, получаем другое выражение теоремы: центр масс системы движется как материальная точка, масса которой равна массе всей системы и к которой приложены все внешние силы, действующие на систему.
Проектируя обе части равенства на координатные оси, получим:
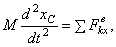

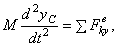
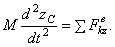
Эти уравнения представляют собою дифференциальные уравнения движения центра масс в проекциях на оси декартовой системы координат.
Значение доказанной теоремы состоит в следующем.
1) Теорема дает обоснование методам динамики точки. Из уравнений видно, что решения, которые мы получаем, рассматривая данное тело как материальную точку, определяют закон движения центра масс этого тела, т.е. имеют вполне конкретный смысл.
В частности, если тело движется поступательно, то его движение полностью определяется движением центра масс. Таким образом, поступательно движущееся тело можно всегда рассматривать как материальную точку с массой, равной массе тела. В остальных случаях тело можно рассматривать как материальную точку лишь тогда, когда практически для определения положения тела достаточно знать положение его центра масс.
2) Теорема позволяет при определении закона движения центра масс любой системы исключать из рассмотрения все наперед неизвестные внутренние силы. В этом состоит ее практическая ценность.
Так движение автомобиля по горизонтальной плоскости может происходить только под действием внешних сил, сил трения, действующих на колеса со стороны дороги. И торможение автомобиля тоже возможно только этими силами, а не трением между тормозными колодками и тормозным барабаном. Если дорога гладкая, то как бы не затормаживали колеса, они будут скользить и не остановят автомобиль.
Или после взрыва летящего снаряда (под действием внутренних сил) части, осколки его, разлетятся так, что центр масс их будет двигаться по прежней траектории.
Теоремой о движении центра масс механической системы следует пользоваться для решения задач механики, в которых требуется:
- по силам, приложенным к механической системе (чаще всего к твердому телу), определить закон движения центра масс;
- по заданному закону движения тел, входящих в механическую систему, найти реакции внешних связей;
- по заданному взаимному движению тел, входящих в механическую систему, определить закон движения этих тел относительно некоторой неподвижной системы отсчета.
С помощью этой теоремы можно составить одно из уравнений движения механической системы с несколькими степенями свободы.
При решении задач часто используются следствия из теоремы о движении центра масс механической системы.
Следствие 1. Если главный вектор внешних сил, приложенных к механической системе, равен нулю, то центр масс системы находится в покое или движется равномерно и прямолинейно. Так как ускорение центра масс равно нулю, 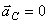 .
.
Следствие 2. Если проекция главного вектора внешних сил на какую-нибудь ось равна нулю, то центр масс системы или не изменяет своего положения относительно данной оси, или движется относительно нее равномерно.
Например, если на тело начнут действовать две силы, образующие пару сил (рис.38), то центр масс С его будет двигаться по прежней траектории. А само тело будет вращаться вокруг центра масс. И неважно, где приложена пара сил.
Кстати, в статике мы доказывали, что действие пары на тело не зависит от того, где она приложена. Здесь мы показали, что вращение тела будет вокруг центральной оси С.
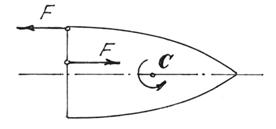
Рис.38
