Закон полного тока в дифференциальной форме
Основным законом, характеризующим свойства магнитного поля, является закон полного тока, который устанавливает связь между напряженностью магнитного поля и током. Он гласит: циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна алгебраической сумме токов, сцепленных с этим контуром:
.
Положительное направление тока связано с направлением обхода контура правилом правого винта. Если обозначить плотность тока 
, то ток, проходящий через поверхность S, ограниченную кривой L,
.
Пользуясь теоремой Стокса можно записать равенство
Следовательно,
Так как это равенство справедливо для всех значений предела интегрирования S, то подинтегральные функции равны между собой:
 . | (43.5) |
Формула (43.5) представляет собой закон полного тока в дифференциальной форме и носит название первого уравнения Максвелла. Оно указывает на то, что магнитное поле является полем вихревым.
Ротор – это функция, характеризующая поле в рассматриваемой точке в отношении способности к образованию вихрей.
Вихревыми принято называть поля, в которых ротор векторной величины, описывающей поле, отличен от нуля. Так как для магнитного поля постоянного тока 
, то во всех точках пространства, где 
, поле вектора 
является вихревым.
В тех же точках пространства, где 
, и соответственно 
, магнитное поле можно рассматривать как потенциальное.
3. Раскрытие выражения rot 
= 
в декартовой системе
Координат
В декартовой системе координатrotраскрывается следующим образом:
 | (43.6) |
4. Раскрытие rot 
= 
в виде определителя в декартовой
Системе
Ротор любого вектора, используемого в теории электромагнитного поля, можно представить в виде определителя третьего порядка. Так, rot 
в декартовой системе записывают в виде следующего определителя:
rot =  . | (43.7) |
Принцип непрерывности магнитного потока
Под магнитным потоком понимают поток вектора магнитной индукции через некоторую поверхность:
 . | (43.8) |
Магнитный поток измеряется в веберах (вб).
Магнитную индукцию можно определить как плотность магнитного потока. Если площадь S перпендикулярна вектору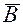 
и поле однородное, то 
Установлено, что магнитный поток сквозь замкнутую поверхность всегда равен нулю:
 | (43.9) |
Пользуясь теоремой Остроградского, можно записать:
Так как это равенство справедливо для любого объема, то
 | (43.10) |
Последняя формула выражает принцип непрерывности магнитного потока в дифференциальной форме. Она означает, что линии магнитной индукции не имеют ни истоков, ни стоков и являются замкнутыми сами на себя линиями.