Диаграммы Венна и операции над множествами
| В большинстве разделов математики понимание сущест-венно облегчается при помощи разнообразных рисунков и диаг-рамм. В рассуждениях о множествах часто используются диаг-раммы Венна, предложенные английским логиком Джоном Венном (1834-1923). В этих диаграммах универсальное множес-тво представлено прямоугольником, а другие рассматриваемые множества - обычно овалами или кружками (размер и форма фигур не имеют значения). Типичный пример диаграммы Венна показан на рис.1. На нём вся область, ограниченная прямоуголь-ником, представляет универсальное множество U, а два овала представляют два множества A и B. Диаграммы Венна дают наг- |  Рис.1. Диаграмма Венна Рис.1. Диаграмма Венна |
лядное представление об операциях над множествами, рассматриваемыми в разделе 2.1.
2.1. Операции над множествами.Если мы располагаем некоторым запасом множеств, то из них мы можем строить новые множества при помощи так называемых теоретико-множественных операций. Рассмотрим подробно основные из этих операции.
A. Дополнение. Пусть U- универсальное множество, A- некоторое множество (напомним ещё раз, что в рамках любой конкретной ситуации каждое множество содержится в универ-сальном для данной ситуации множестве U, т.е. AÍU). Множес-тво, состоящее из всех элементов U, не содержащихся в A, на-зывают дополнениемAи обозначают через A'. Более формаль-но: хÎA' 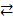 хÏA. Диаграмма Венна на рис.2 иллюстрирует опе-рацию дополнения. B. Объединение.Множество, элементами которого явля-ются элементы множеств A и B и только они, называют их объе-динением и обозначают знакосочетанием A хÏA. Диаграмма Венна на рис.2 иллюстрирует опе-рацию дополнения. B. Объединение.Множество, элементами которого явля-ются элементы множеств A и B и только они, называют их объе-динением и обозначают знакосочетанием A 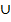 B. Очевидно: (хÎA B. Очевидно: (хÎA 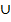 B) B) 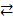 (хÎA)Ú(хÎB). Объединением семейства множеств {Ai}iÎI называют множество, обозначаемое знакосочетанием (хÎA)Ú(хÎB). Объединением семейства множеств {Ai}iÎI называют множество, обозначаемое знакосочетанием 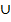 iÎI Ai и состоящее из тех и только тех элементов, каждый из которых принадлежит хотя бы одному множеству этого семейства. Ди-аграмма Венна на рис.3 иллюстрирует операцию объединения. iÎI Ai и состоящее из тех и только тех элементов, каждый из которых принадлежит хотя бы одному множеству этого семейства. Ди-аграмма Венна на рис.3 иллюстрирует операцию объединения. |  Рис.2. Дополнение Рис.2. Дополнение |
 Рис.3. Объединение Рис.3. Объединение | |
C. Пересечение. Множество, элементами которого явля-ются элементы, принадлежащие как множеству A, так и мно-жеству B, называют их пересечением и обозначают знакосоче-танием A∩B. Очевидно: (хÎA 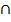 B) B) 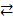 (хÎA)Ù(хÎB). Пересечением семейства множеств {Ai}iÎI называют множество, обозначаемое знакосочетанием (хÎA)Ù(хÎB). Пересечением семейства множеств {Ai}iÎI называют множество, обозначаемое знакосочетанием 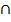 iÎIAi и состоящее из тех и только тех элемен-тов, каждый из которых принадлежит всем множествам этого семейства. Диаграмма Венна на рис.4 иллюстрирует операцию пересечения. D. Разность. Множество, элементами которого являются элементы множества A, не принадлежащие множеству B, назы-вают их разностью и обозначают знакосочетанием A iÎIAi и состоящее из тех и только тех элемен-тов, каждый из которых принадлежит всем множествам этого семейства. Диаграмма Венна на рис.4 иллюстрирует операцию пересечения. D. Разность. Множество, элементами которого являются элементы множества A, не принадлежащие множеству B, назы-вают их разностью и обозначают знакосочетанием A  B (саму операцию называют вычитанием множеств). Очевидно: (хÎA B (саму операцию называют вычитанием множеств). Очевидно: (хÎA  B) B) 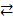 (хÎA)Ù(хÏB). Если, в частности, BÍA, то разность A (хÎA)Ù(хÏB). Если, в частности, BÍA, то разность A  B на-зывают дополнением множества B до множества A и обозна-чают через (B')A, или просто B', если ясно, о чём идет речь. Ди-аграмма Венна на рис.4 иллюстрирует операцию вычитания и её результат.. E. Симметрическая разность.Множество, элементами которого служат элементы множества A, не принадлежащие множеству B, и элементы множества B, не принадлежащие мно-жеству A, называют их симметрической разностью и обозна-чают знакосочетанием AΔB. Очевидно: (хÎA B на-зывают дополнением множества B до множества A и обозна-чают через (B')A, или просто B', если ясно, о чём идет речь. Ди-аграмма Венна на рис.4 иллюстрирует операцию вычитания и её результат.. E. Симметрическая разность.Множество, элементами которого служат элементы множества A, не принадлежащие множеству B, и элементы множества B, не принадлежащие мно-жеству A, называют их симметрической разностью и обозна-чают знакосочетанием AΔB. Очевидно: (хÎA  B) B) 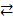 ((хÎA)Ù(хÏB)) ((хÎA)Ù(хÏB))  . По определению, AΔB = (A . По определению, AΔB = (A  B) B) 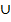 (B (B  A). Диаг-рамма Венна на рис.6 иллюстрирует симметрическую разность. A). Диаг-рамма Венна на рис.6 иллюстрирует симметрическую разность. |  Рис.4. Пересечение Рис.4. Пересечение |
 Рис.5. Разность Рис.5. Разность | |
 Рис.6. Симметрическая разность Рис.6. Симметрическая разность |
