Граничные условия для векторов электромагнитного поля
В электромагнитном поле вектора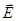 
и 
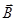меняются в фазе. Закон изменения – гармонический, т.е. зависимость во времени и пространстве характеризуется косинусом.
В однородной изотропной среде, где нет границ раздела, электромагнитная волна распространяется прямолинейно, в направлении перпендикуляра к волновому фронту.
Если есть две среды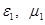 
и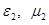 
, то вектор 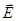падающей волны может быть произвольно ориентирован относительно поверхности раздела. Принято рассматривать раздельно нормальную и тангенциальные составляющие в 1-й и во 2-й средах.
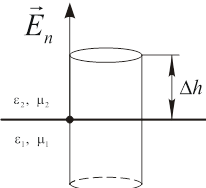
1). Нормальная составляющая.
, 
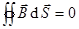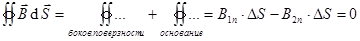(т.к. интеграл по боковой поверхности стремится к нулю при 
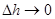). Т.о., из последнего уравнения:
,
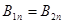т.е. нормальная составляющая вектора 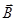непрерывна,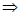 
,
,
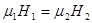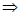
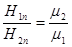а нормальная составляющая вектора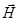 
испытывает разрыв.
Для составляющей электрического поля используем III уравнение Максвелла: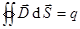 
. Рассматривая нейтральную границу раздела (т.е. 
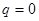), получаем данный интеграл 
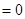и аналогично
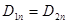, и
.
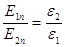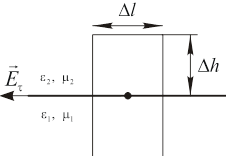2). Тангенциальные составляющие векторов.
Рассмотрим замкнутый контур. Пусть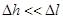 
, причем 
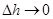. Тогда
,
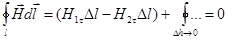откуда получаем (т.к. второй интеграл ):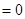
.
, 
.
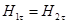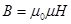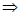
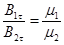Аналогично, рассматривая тангенциальную составляющую электрического поля, получим:
,
.
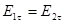
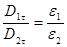