Магнитный поток. Теорема Гаусса и закон полного тока

Введем аналогично тому, как это было сделано в электростатике, понятие о потоке вектора магнитной индукции.

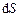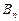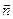Потоком вектора магнитной индукции, или магнитным потоком, сквозь некую площадку называется физическая величина равная произведению величины этой площадки и проекции вектора на направление нормали к площадке :

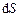– через элементарную площадку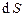

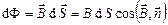; (3.38)

– через произвольную поверхность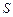

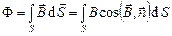, (3.39)

где 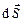– вектор, численно равный площади 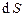и направленный вдоль нормали 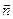к поверхности (рис. 3.19).

Если магнитное поле остается однородным в пределах плоской площадки 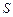, то

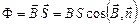. (3.40)

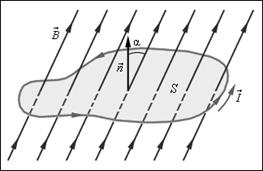
Рис. 3.19 Магнитный поток через замкнутый контур. Направление нормали 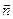и выбранное положительное направление обхода контура 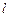связаны правилом правого винта

В СИединица магнитного потока называется Вебером (Вб)

.

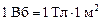Потокосцепление (полный поток) – магнитный поток через все витки катушки, рамки и т. п.

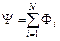. (3.41)

Если магнитные потоки через все витки одинаковы, то

,

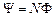где 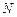– число витков контура; 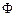– магнитный поток через один виток. Эта формула справедлива для соленоида и тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

Рассмотрим замкнутую поверхность и пересекающий ее поток (рис. 3.19). Как и в электростатике будем приписывать выходящему потоку положительный знак, а входящему – отрицательный. Поскольку в природе нет магнитных зарядов, то линии магнитной индукции не имеют начала и конца и являются замкнутыми. Поэтому число линий входящих с одной стороны поверхности в точности равно числу линий выходящих с другой ее стороны и, следовательно, суммарный поток равен нулю.

Тогда можно сформулировать теорему Гаусса для магнитного поля в интегральной форме: магнитный поток сквозь произвольную замкнутую поверхность равен нулю.

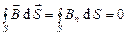. (3.42)

Рассматривая контур в виде окружности, охватывающей бесконечный прямолинейный проводник с током (рис. 3.20), вычислим циркуляцию вектора по этому контуру (считаем μ = 1): .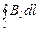

Физический смысл циркуляции состоит в том, что поскольку магнитная индукция ‑ силовая характеристика магнитного поля, то циркуляция будет определять работу сил магнитного поля по замкнутому контуру.

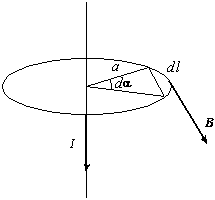
Рис. 3.20 Определение циркуляции прямолинейного тока

Учитывая, что

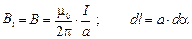, (3.43)

получим

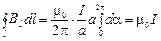, (3.44)

т. е. циркуляция вектора индукции по замкнутому контуру равна произведению m₀ на ток, охватываемый этим контуром.

Как оказывается, полученное выражение (3.44) справедливо для контуров любой формы.

То, что циркуляция вектора магнитной индукции по замкнутому контуру отлична от нуля, выражает вихревой характер магнитного поля.

Если контур охватывает несколько проводников с токами, то циркуляция вектора индукции суммарного магнитного поля равна сумме этих токов:

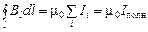, (3.45)

где полный ток

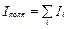. (3.46)

Условимся о направлении обхода контуров и знаке токов: положительными будем считать токи, направление которых связано с направлением обхода контура правилом правого винта; токи противоположного направления считаем отрицательными. Если обход контура совершается не один, а n раз, то выражение (3.45) примет вид

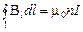. (3.47)

Формулы (3.45) и (3.47) позволяют сформулировать закон полного тока (теорема о циркуляции вектора ). Циркуляция вектора магнитной индукции вдоль произвольного замкнутого контура 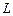равна произведению магнитной постоянной 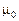на алгебраическую сумму сил токов, охватываемых этим контуром. Сила тока считается положительной, если направление тока связано с направлением обхода по контуру правилом правого винта (рис. 3.21).

Таким образом, в вакууме закон полного тока запишется следующим образом

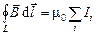, (3.48)

где 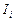– сила тока проводимости, охватываемого контуром .

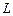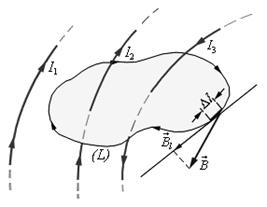
Рис. 3.21 Теорема о циркуляции

В магнитной среде – закон полного тока для магнитной индукции и напряженности:

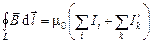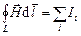; , (3.49)

где 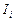и 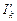– силы токов проводимости и намагничивания, охватываемые контуром .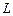