Задания для контрольной работы
Задания для контрольной работы по теме «Ряды Фурье»
Задание 1.
Разложить в ряд Фурье периодическую (с периодом Т = 2π) функцию f(х), заданную на отрезке [-π ; π].
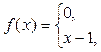
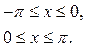
Задание 2.
Разложить в ряд Фурье периодическую (с периодом 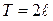 ) функцию f(х), заданную на отрезке [-
) функцию f(х), заданную на отрезке [- 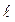 ;
; 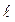 ].
].
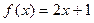 , [-3; 3]; T = 6.
, [-3; 3]; T = 6.
Задание 3.
На заданном отрезке разложить в ряд Фурье периодическую функцию 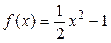 ,[-π; π ]; T = 2π.
,[-π; π ]; T = 2π.
Задание 4.
Разложить в ряд Фурье функцию f(х), заданную на полупериоде [0; 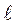 ], продолжив (доопределив) ее четным и нечетным образом.
], продолжив (доопределив) ее четным и нечетным образом.
Построить графики функций.
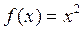 , [0; π].
, [0; π].
Задание 5.
Разложить в ряд Фурье функцию, заданную графиками
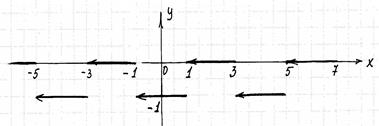
Рисунок 22
Задание 6.
Представить комплексной формой ряда Фурье функцию f(х) периода 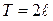 , заданную на указанном интервале.
, заданную на указанном интервале.
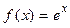 , (-3; 3), T = 2.
, (-3; 3), T = 2.
Задания для контрольной работы по теме «Численные методы»
2. 1. Методом половинного деления уточнить корни уравнения 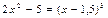 на промежутке [5;6] с точностью до 0,01.
на промежутке [5;6] с точностью до 0,01.
3. Отделить корни уравнения 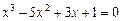 графически и программно. Уточнить корни уравнения методом хорд, методом касательных, комбинированный метод хорд и касательных с точностью
графически и программно. Уточнить корни уравнения методом хорд, методом касательных, комбинированный метод хорд и касательных с точностью 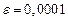 . Нарисовать схему применения метода к каждому корню уравнения.
. Нарисовать схему применения метода к каждому корню уравнения.
4. Уточнить один из корней уравнения 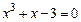 методом итерации с точностью
методом итерации с точностью 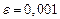 , указать число итераций. Нарисовать схему применения метода итерации к данному корню уравнения.
, указать число итераций. Нарисовать схему применения метода итерации к данному корню уравнения.
5. По заданной таблице значений функции составить интерполяционный многочлен Лагранжа и построить его график.
| x0 | x1 | x2 | x3 | y0 | y1 | y2 | y3 |
| -1 | -3 |
6. Найти приближенное значение функции при заданном значении аргумента 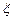 с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах;
с помощью соответствующего интерполяционного полинома Ньютона, если функция задана в равноотстоящих узлах; 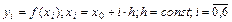 ,
, 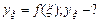 Оценить погрешность полученного значения.
Оценить погрешность полученного значения.
| хi | 1,15 | 1,30 | 1,45 | 1,60 | 1,75 | 1,90 | |
| уi | 0,9950 | 1,1424 | 1,2890 | 1,4348 | 1,5796 | 1,7233 | 1,8658 |
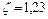
7. Апроксимировать методом наименьших квадратов функции, заданные таблично:
| х | 0,43 | 0,48 | 0,55 | 0,62 | 0,70 | |
| у | 1,63 | 1,73 | 1,87 | 2,03 | 2,22 |
8. Построить кубический сплайн для функции, заданной в узлах интерполяции, предполагая, что сплайн имеет нулевую кривизну при х = х0 и х = х4. Вычислить значение функции в точке х = Х*.
| Х*=1,5 | х | 1,0 | 1,0 | 2,0 | 3,0 | 4,0 |
| у | 0,0 | 0,5 | 0,86603 | 1,0 | 0,86603 |
9. Вычислить интеграл 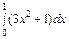 , приняв шаг интегрирования
, приняв шаг интегрирования 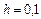 , с помощью:
, с помощью:
1) формул прямоугольника;
2) формулы трапеций;
3) формулы Симпсона;
4) сравнить полученные результаты с точным решением (найти его самостоятельно), определить абсолютную и относительную погрешности каждого метода.
Критерии оценки:
- оценка «отлично» (17-20 б) выставляется студенту, если работа выполнена полностью; в логических рассуждениях и обосновании решения нет пробелов и ошибок; в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания учебного материала);
- оценка «хорошо» (14-17 б) выставляется студенту, если работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки); допущена одна ошибка или два-три недочета в выкладках.
ТЕСТОВЫЕ ЗАДАНИЯ
| 1. Запишите правильный ответ A - точное значение числа, а - приближенное. Найти абсолютную погрешность приближения, если А=8,3 , а=8,325 | |||||||||||||
| 2. Запишите правильный ответ A - точное значение числа, а - приближенное. Найти абсолютную погрешность приближения, если А=14,7, а=14,82 | |||||||||||||
| 3. Запишите правильный ответ A - точное значение числа, а - приближенное. Найти абсолютную погрешность приближения, если А=25,9, а=26 | |||||||||||||
| 4. Округлите с точностью до 0,1 число 12,285 | 1) 12,2 2) 12,29 3) 12,3 4) 12 | ||||||||||||
| 5.Округлите с точностью до 0,01 число5,145 | 1) 5,2 2) 5,15 3) 5,14 4) 5,1 | ||||||||||||
| 6. Округлите с точностью до целых361,25 | 1) 361,2 2) 362 3) 362,3 4) 361 | ||||||||||||
| 7. Приближенное значение числа А равно а = 71. Абсолютная погрешность этого приближения равна 0,71. Найти относительную погрешность | 1) 0,01 2) 0,001 3) 1% 4) 10% | ||||||||||||
| 8. Приближенное значение числа А равно а=5. Относительная погрешность этого приближения равна 0,001. Найти абсолютную погрешность. | 1) 0,5 2) 0,05 3) 0,005 4) 0,0005 | ||||||||||||
| 9. Указать интервал изоляции корня по таблице
| 1) [ 1; 2] 2) [ -8; 1] 3) [ 1; -8] 4) [ 2; 1] | ||||||||||||
| 10. Указать интервал изоляции корня по таблице
| 1) [ 0; 1] 2) [ 8; -1] 3) [ 1; 2] 4) [ 2; -1] | ||||||||||||
| 11. Указать интервал изоляции корня по таблице
| 1) [ 3; -3] 2) [ 2; 3] 3) [ 4; -6] 4) [ 6; -3]. | ||||||||||||
12. Укажите, какой метод приближенного решения уравнения иллюстрирует данный рисунок: 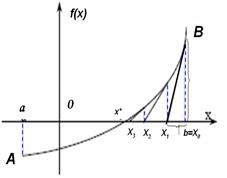 | 1) Метод половинного деления 2) Метод хорд 3) Метод касательных | ||||||||||||
13. Укажите, какой метод приближенного решения уравнения иллюстрирует данный рисунок: 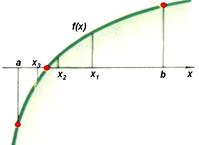 | 1) Метод половинного деления 2) Метод хорд 3) Метод касательных 4) Метод итераций | ||||||||||||
14. Укажите, какой метод приближенного решения уравнения иллюстрирует данный рисунок: 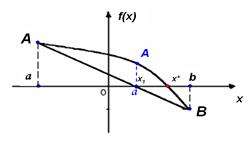 | 1) Метод половинного деления 2) Метод хорд 3) Метод касательных 4) Метод итераций | ||||||||||||
| 15. Установите соответствие, какому численному методу решения уравнений соответствуют данные формулы: 1) Метод половинного деления 2) Метод хорд 3) Метод касательных 4) Комбинированный метод хорд и касательных | а) 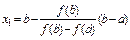 б) б) 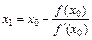 в) в) 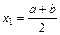 | ||||||||||||
16. Установите для данного численного метода решения уравнений соответствующую формулу: 1) 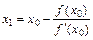 ; 2) ; 2) 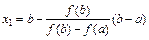 ; 3) ; 3) 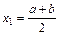 . . | а) Метод половинного деления б) Метод хорд в) Метод дихотомии г) Метод касательных | ||||||||||||
| 17. Уточнить корень уравнения f(x)=0 методом половинного деления
| 1) 1,25 2) 1,5 3) 1,75 | ||||||||||||
| 18. Уточнить корень уравнения f(x)=0 методом половинного деления
| 1) 4 2) 3,5 3) 0 1) 0,5 2) 1 3) 1,5 | ||||||||||||
| 19. Уточнить корень уравнения f(x)=0 методом половинного деления
| |||||||||||||
| 20. Уточнить корень уравнения f(x)=0 методом хорд
| 1) 2,8 2) 3 3) 3,4 | ||||||||||||
| 21. Уточнить корень уравнения f(x)=0 методом хорд
| 1) 0,6 2) 0,5 3) 1,4 | ||||||||||||
| 22. Уточнить корень уравнения f(x)=0 методом хорд
| 1) 3,3 2) 3,5 3) 3,4 | ||||||||||||
23. Уточните корень методом касательных:
| |||||||||||||
24. Уточните корень методом касательных:
| |||||||||||||
25. Уточните корень методом касательных:
Наши рекомендацииЧисло: 2085 |
