Свойства простейшего пуассоновского потока

ординарность(в каждый момент времени в СМО может пос­тупать не более одной заявки). Ординарность потока означает, что вероятность попадания на элементарный участок Dt двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него ровно одного события, т.е. при Dt->0 эта вероятность представляет собой бесконечно малую высшего порядка.

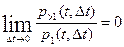
В каждый момент времени в СМО может пос­тупать не более одной заявки

Примерами ординарных потоков событий могут служить поток деталей, поступающих на конвейер для сборки, поток отказов технического устройства, поток автомашин, прибывающих на станцию техобслуживания. Примером неординарного потока может служить поток пассажиров, прибывающих в лифте на данный этаж.

Для ординарного потока можно пренебречь возможностью совместного появления на элементарном участке двух и более событий. В каждый момент времени в СМО может пос­тупать не более одной заявки

отсутствие последействия - для любых не перекрывающихся участков времени T₁,T₂,…,T_n числа событий Х₁=Х(t₁,T₁),Х₂=Х(t₂,T₂),…., Х_n = Х(t_n,T_n), попадающих на эти участки, представляют собой независимые случайные величины, т.е. вероятность попадания любого числа событий на один из участков не зависит от того, сколько их попало на другие.

Отсутствие последействия означает, что для любого момента времени t0, будущие моменты наступления события потока (при t>t0) не зависят от того, в какие моменты наступали события в прошлом (при t<t0).

Ординарный поток событий, в котором отсутствует последействие, называется пуассоновским потоком.

Стационарность

Поток событий называется стационарным, если все его вероятностные характеристики не меняются со временем. В частности, для стационарного потока событий вероятность попадания того или иного числа событий на участок длины T

зависит только от длины этого участка и не зависит от того, где именно на оси времени 0t этот участок расположен.

Это значит, что числа событий Х₁(t₁, T) и Х₂(t₂, T), попадающих на два участка одинаковой длины T, будут иметь одинаковые распределения. Отсюда следует, в частности, что для стационарного потока событий его интенсивность l(t) постоянна:

l(t) = l = const

Поток событий, обладающий всеми тремя свойствами, называется простейшим (или стационарным пуассоновским потоком).

Кроме того, к достоинствам простейшего потока можно так­же отнести следующее:

а) Сумма N независимых, ординарных и стационарных пото­ков заявок с интенсивностями 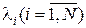сходится к простейшему потоку с интенсивностью 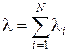, при условии, что складываемые потоки оказывают более или ме­нее одинаково малое влияние на суммарный поток;

б) Поток заявок, полученный путем случайного разрежения
исходного потока, когда каждая заявка с определенной
вероятностью p исключается из потока независимо от того, исключены другие заявки или нет, образует простейший поток с интенсивностью 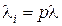, где 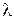- интенсивность исходного потока. В отношении исходного потока заявок делается предположение лишь об ординарности и стационар­ности.

Поток с ограниченным последействием (рекуррентный поток) – поток, у которого случайные интервалы t1, t2,…, tn между соседними по времени событиями представляют собой независимые случайные величины. При его моделировании применяется последовательная (рекуррентная процедура): сначала разыгрывается величина t1, затем t2 и т.д. Например, последовательность вызовов такси.

Поток без последействия является частным случаем потока с ограниченным последействием.

Поток Пальма. Стационарный поток с ограниченным последействием называется потоком Пальма. Для такого потока интервалы t1, t2,…, tn между соседними событиями представляют собой последовательность независимых, одинаково распределенных СВ.

Простейший пуассоновский поток является потоком Пальма. У простейшего потока интервалы t1, t2,…, tn распределены одинаково, по показательному закону и независимы между собой. Поток Пальма отличный от простейшего получается, если интервалы между событиями распределены по другому закону.