Функція Ґріна оператора Лапласа

Нехай у тривимірному просторі задана обмежена поверхнею S область D. Припустимо, що функція U(M), M=M(x,y,z) гармонічна в D і належить класу .

Визначення.Функція G(P,M), називається функцією Ґріна задачі Діріхле для рівняння Лапласа, якщо для неї справджуються наступні умови:

1) G(P,M) як функція точки є гармонічною в області Dза винятком точки M, де вона перетворюється в нескінченість;

2) G(P,M) як функція точки справджує крайову умову

3) в області Dфункція G(P,M) допускає подання у вигляді

де g(P,M) – гармонічна всюди в області Dфункція, яка визначається з задачі Діріхле

- 64 -

Якщо функція G(P,M) відома, то розв’язок внутрішньої задачі Діріхле

якщо він існує, дається формулою

де 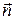– зовнішня нормаль до поверхні Sу точці Р.

Якщо маємо задачу Діріхле для рівняння Пуассона

причому то

Зауваження. У випадку площини функція Ґріна має вигляд

а її реґулярна частина g(P,M) визначається з задачі Діріхле (тут D– плоска область, а S– замкнута крива, яка обмежує цю область)

Основні властивості функції Ґріна:

1) G(P,M) невід’ємна в області D;

2) G(P,M) є симетричною відносно точок Р та М, тобто G(P,M)=G(М,Р).

Теорія потенціалу

Нехай у деякій точці A(a,b,c) тривимірного простору розміщений електричний заряд q. На підставі закону Кулона можна показати (див. [4], розділ ІV, тема 3), що точковий заряд величини q в довільній точці M(x,y,z) простору створює потенціал

Легко бачити, що при (чим далі від джерела, тим слабша дія заряду).

Поскільки при наявності кількох точкових зарядів створювані ними потенціали сумуються, то загальний потенціал, створений рівномірно розподіленим зарядом, знаходиться як границя суми, тобто у вигляді інтеґрала.

- 65 -

Розглянемо основні види потенціалів та їх властивості.

1. Об’ємний потенціал. Потенціал, створений зарядом, розподіленим по об’єму D тривимірного простору з об’ємною густиною f(M), рівний

Тут – довільна (біжуча) точка об’єму D, M=M(x,y,z) – деяка (фіксована) точка тривимірного простору.

Потенціал об’єму є гармонічною функцією зовні області D, тобто при справджує рівняння Лапласа .

Теорема 1. Якщо об’ємна густина f(M) є обмеженою й інтеґровною в області D функцією, то потенціал об’єму V(M) і його частинні похідні першого порядку є неперервними у всьому просторі, причому ці похідні можуть бути одержані шляхом диференціювання під знаком інтеґрала.

Теорема 2. Якщо об’ємна густина то потенціал об’єму V(M) має неперервні похідні другого порядку в області Dі при справджує рівняння Пуассона

Наслідок. Якщо об’ємна густина f(M) справджує умови теореми 2, то рівняння має частинний розв’язок

2. Потенціал простого шару. Якщо заряд розподілений по поверхні Sіз поверхневою густиною то потенціал, створюваний цим зарядом, рівний

де – довільна (біжуча) точка на поверхні S, M=M(x,y,z) – деяка (фіксована) точка тривимірного простору.

У всіх точках M(x,y,z) простору, які не належать поверхні S, потенціал простого шару має похідні всіх порядків і справджує рівняння Лапласа, причому при .

Теорема 3. Потенціал простого шару з неперервною густиною є неперервною функцією у всьому просторі.

Похідна по напряму зовнішньої нормалі до поверхні Sу фіксованій точці дається формулою

(24)

- 66 -

Позначимо і границі похідної по напряму , коли відповідно зсередини та ззовні поверхні S. Тоді мають місце формули:

(25)

Отже, у точках поверхні нормальна похідна потенціалу простого шару має скачок:

(26)

Зауваження. У випадку площини, якщо заряд розподілений по деякій замкнутій кривій із лінійною густиною одержимо лоґарифмічний потенціал простого шару:

де – довільна (біжуча) точка на кривій , M=M(x,y) – деяка (фіксована) точка площини.

Формули (24)-(26) для лоґарифмічного потенціалу простого шару матимуть вигляд:

де – деяка фіксована точка кривої .

За допомогою потенціалів простого шару будуються розв’язки задач Неймана (друга крайова задача) для рівняння Лапласа.

3. Потенціал подвійного шару. Нехай S– орієнтована поверхня (тобто на ній вказані внутрішня та зовнішня сторони), по якій розподілений диполь із

- 67 -

густиною моментів причому в кожній точці напрям осі диполя співпадає з напрямом внутрішньої нормалі до поверхні Sу точці Р.

Потенціал, створюваний диполем, рівний

(27)

Формулу потенціалу подвійного шару (27) можна записати в іншому вигляді:

Тут M=M(x,y,z) – фіксована точка простору; 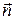– напрям зовнішньої нормалі до поверхні Sу точці Р.

При потенціал подвійного шару має похідні усіх порядків і справджує рівняння Лапласа, причому при .

Теорема 4. Потенціал подвійного шару (27) має границі при прямуванні точки М до фіксованої точки ззовні або зсередини. Якщо границю значень ззовні позначити через а границю зсередини – через то мають місце формули:

(28)

(29)

тобто величина скачка функції у довільній точці буде

(30)

Інтеґрал називається прямим значенням потенціалу подвійного шару в точці .

Зауваження. У випадку площини, якщо диполь розподілений по деякій замкнутій орієнтованій кривій з густиною моментів одержимо лоґарифмічний потенціал подвійного шару:

де – довільна (біжуча) точка на кривій , M=M(x,y) – деяка (фіксована) точка площини.

Формули (27)-(30) для лоґарифмічного потенціалу подвійного шару матимуть вигляд:

- 68 -

За допомогою потенціалів подвійного шару будуються розв’язки задач Діріхле (перша крайова задача) для рівняння Лапласа.

ПРИКЛАД 1.Знайти лоґарифмічний потенціал простого шару відрізка зі сталою густиною заряду

Розв’язання. Згідно визначення лоґарифмічний потенціал простого шару дається формулою

Тут: – відрізок ; М(х,у) – фіксована точка площини; Р(ξ,0) – точка відрізка ; Отже,

ПРИКЛАД 2. Користуючись поверхневими потенціалами, знайти розв’язок задачі Діріхле для рівняння Лапласа у півпросторі:

Розв’язання. Розв’язок першої крайової задачі для рівняння Лапласа шукається у вигляді потенціалу подвійного шару:

Для даного прикладу:

- 69 -

S – площина хОу; М(х,у,z) – фіксована точка простору; Р(ξ,η,0) – точка площини хОу;

Зауважимо, що зовнішня нормаль 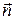до площини хОу в точці Р на-прямлена протилежно до осі Оz, поскільки – “внутрішня” сторона площини. Отже, будемо мати

(31)

Невідому густину моментів визначаємо із властивості скачка потенціалу подвійного шару (28):

Звідси, враховуючи, що а (нормаль 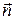перпендикулярна до площини хОу), одержимо тобто для довільної точки А тоді згідно формули (31)

КОНТРОЛЬНІ ПИТАННЯ

1.Які фізичні процеси приводять до крайових задач для рівнянь еліптичного типу?

2.Дайте визначення гармонічної функції:

а) в обмеженій області;

б) в необмеженій області.

3.Запишіть постановку

а) задачі Діріхле для рівняння Лапласа у півкрузі 0≤ρ≤R, 0≤φ≤π;

б) задачі Неймана для рівняння Лапласа у кільці а≤ρ≤b, 0≤φ<2π;

в) третьої крайової задачі для рівняння Пуассона у прямокутнику 0≤х≤1, 0≤у≤4.

4.Запишіть оператор Лапласа у полярних, циліндричних та сферичних координатах.

5.Сформулюйте принцип мінімакса для гармонічних функцій.

6.Сформулюйте теореми про розв’язок

а) задачі Діріхле;

б) задачі Неймана.

- 70 -

7.У чому суть умови стаціонарності теплового поля?

8.У чому полягає метод власних функцій знаходження розв’язків крайових задач для рівнянь еліптичного типу в прямокутнику?

9.Як будується розв’язок крайових задач для рівняння Лапласа: а) у крузі; б) в кільці; в) у круговому секторі?

10.Які з функцій:

можуть бути розв’язками внутрішньої (зовнішньої) задачі Діріхле для круга і чому?

11.Запишіть умову стаціонарності теплового поля:

а) для кільця а≤ρ≤b, 0≤φ<2π;

б) для кругового сектора 0≤ρ≤а, 0≤φ≤α<2π;

в) для квадрата 0≤х, у≤с.

12.При яких значеннях сталої А будуть коректно поставленими задачі Неймана:

а)

б)

13.Як будуються розв’язки крайових задач для рівняння Пуассона в кругових областях?

14.Відомо, що розв’язок деякої задачі Неймана для рівняння Пуассона в півкільці а≤ρ≤b, 0≤φ≤π не залежить від полярного кута. Що ви можете сказати про

а) крайові умови у вихідній задачі;

б) вільний член у рівнянні Пуассона?

15.Запишіть інтеґрал Пуассона задачі Діріхле для рівняння Лапласа всередині та зовні круга 0≤ρ≤R.

16.Сформулюйте основні властивості гармонічних функцій.

17.Дайте визначення функції Ґріна оператора Лапласа.

18.Запишіть інтеґрал для обчислення:

а) об’ємного потенціалу;

б) потенціалів простого та подвійного шару;

в) лоґарифмічних потенціалів простого та подвійного шару.

19.Сформулюйте основні властивості:

а) об’ємного потенціалу;

б) потенціалу простого шару;

в) потенціалу подвійного шару.

- 71 -

20.Які крайові задачі для рівнянь еліптичного типу можна розв’язувати за допомогою потенціалів?