Утверждение. Ранг матрицы равен числу ненулевых строк в матрице, полученной в результате эквивалентных преобразований после получения нулей ниже главной ди- агонали матрицы

Примеры. Найти ранги следующих матриц:

1. ˜

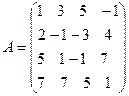Получим нули в первом столбце. Для этого умножим первую строку на (-1) и прибавим к второй строке; умножим ту же строку на (-5) и прибавим к третьей строке и, аналогично, ум- ножим её на (-7) и прибавим к четвёртой строке. Получим:

˜ ˜

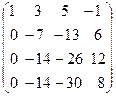Умножим вторую строку на (-2) и прибавим соответственно к третьей и четвёртой

˜ ˜ .

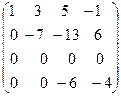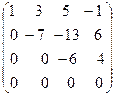Следовательно ранг этой матрицы .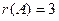

2. ˜

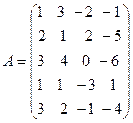С помощью первой строки получим нули в первом столбце. Для этого умножим её на (-2) и прибавим к второй строке, умножим на (-3) и прибавим к третьей и пятой строке, умно- жим на (-1) и прибавим к четвёртой строке. В результате получим:

˜ ˜

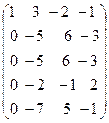Вторую строку умножим на (-1) и прибавим к третьей, чет -вёртую строку умножим на (-4) и прибавим к пятой:

˜ ˜

Пятую строку умножим на (5) и прибавим к второй и умножим на (2) и прибавим к четвёртой:

˜ ˜

четвёртую строку умножим на (-3) и прибавим к второй:

˜ ˜ .

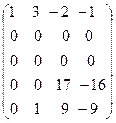Ранг этой матрицы тоже равен .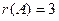

При исследовании систем важную ролю играет следующая теорема:

ТЕОРЕМА (Кронекера – Капелли). Ранг основной матрицы системы не превосходит ранга расширенной матрицы, т.е.

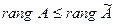, причём, если 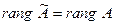, то система совместна, а если 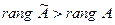, то система несовместна (не имеет решений.

Рассмотрим пример.

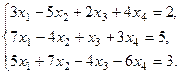
Тогда

˜

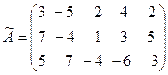Умножим первую строку на (-2) и прибавим к второй и треть- ей строке; после этого поменяем местами первую и вторую строки:

˜ ˜ ˜

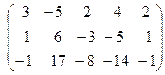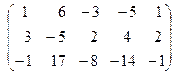прибавим к второй, а после этого прибавим к третьей:

˜ ˜

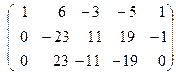После этого прибавим вторую строку к третьей и получим матрицу:

˜ .

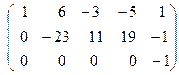В результате получили матрицу, у которой

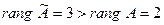, следовательно, система несовместна. Решений нет.

Если 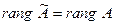, т.е, если система совместна, то в случае, если 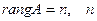- число неизвестных, система имеет единственное решение. Если же 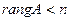, то система имеет бесконечно много решений, при этом число свободных переменных (т.е. переменных, через которые можно выразить все остальные и которые могут принимать любые значения из множества действительных чисел) 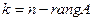, а число ба -зисных переменных (т.е. таких переменных, которые выражаем через свободные) равно .

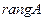Рассмотрим примеры: решить системы уравнений методом Гаусса; найти общие и частные решения; сделать проверку.

1.

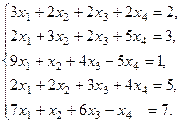
Запишем расширенную матрицу данной системы:

˜

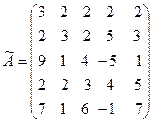Уменьшим элементы первого столбца с помощью четвёртой строки. Для этого умножим её на (-1) и прибавим к первой и второй строке; умножим на (-4) и прибавим к третьей строке и, наконец, умножим на (-3) и прибавим к пятой строке.

˜ ˜

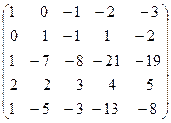Теперь получим нули в первом столбце. Умножим первую строку на (-1) и прибавим к третьей и пятой строке; умножим её же на (-2) и прибавим к четвёртой строке. Получим:

˜ ˜

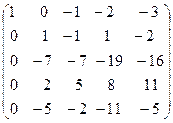С помощью второй строки получим нули во втором столбце. Для этого умножим её на (7) и прибавим к третьей строке; умножим на (-2) и прибавим к четвёртой строке; умножим на (5) и прибавим к пятой строке:

˜ ˜

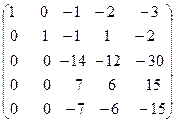Четвёртую строку умножим на (2) и прибавим к третьей строке и её же просто прибавим к пятой строке:

˜ .

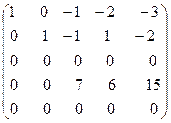Видим, что в данном случае 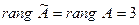, поэтому система совместна, но так как переменных 4, а ранг матрицы равен 3, то одна переменная свободная, а три базисных. За – пишем полученную систему:

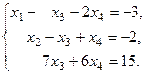
Выберем свободную переменную 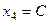, тогда из третьего уравнения 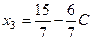; из второго уравнения

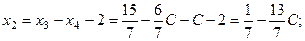
из первого уравнения

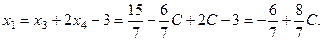
Таким образом, общее решение системы имеет вид:

,

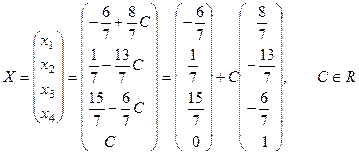т.е. при любом значении 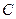мы будем получать решения сис -темы. Это общее решение Задавая какие – либо значения по -стоянной 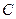, будем получать частные решения. Например, при 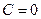получаем частное решение

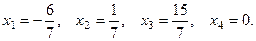
Сделаем проверку:

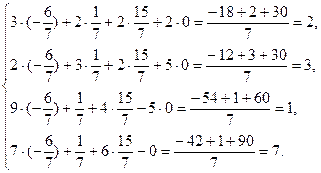
Получили тождественные равенства. Аналогично можно полу- чать другие частные решения и делать проверку. Например, при 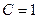: 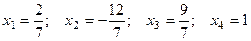. Подставив эти значения в уравнения системы, снова получим тождес -твенные равенства. Таким же образом, при разных значениях 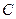можем получить любое частное решение системы.

Ещё одна система:

2.

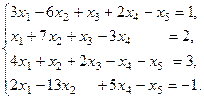
Её расширенная матрица имеет вид:

˜

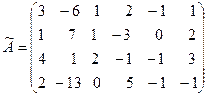Поменяем местами первую и вторую строки:

˜ ˜

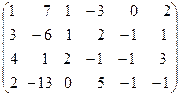С помощью первой строки получим нули в первом столбце. Для этого умножим её на (-3) и прибавим к второй строке; умножим на (-4) и прибавим к третьей строке; умножим на

(-2) и прибавим к четвёртой строке, получим:

˜ ˜

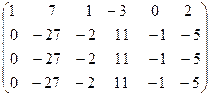Вторую строку умножим на (-1) и прибавим к третьей и чет –вёртой, получим

˜ .

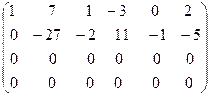Видим, что ранг полученной матрицы равен

.

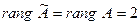Поэтому система совместна. Число базисных переменных рав- но рангу матрицы, т.е. две базисные переменные Число сво -бодных переменных равно разнице «число переменных» = 5 минус «ранг матрицы» = 2, т.е 3 свободные переменные.

Запишем полученную систему:

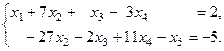
В качестве базисных переменных, если есть возможность, удобно выбрать переменные с единичными коэффициентами, чтобы избежать вычислений с дробными выражениями. Напри- мер, в данном примере, в качестве базисных можем выбрать 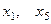, а остальные считать свободными, т.е. положим:

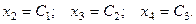
Тогда из второго уравнения:

,

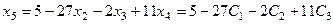а из первого уравнения:

.

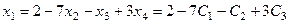Следовательно, общее решение имеет вид:

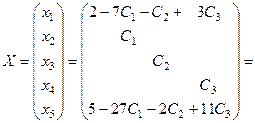
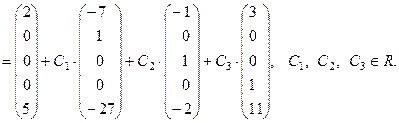
Запишем частное решение и сделаем проверку. Например, при 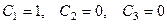получим:

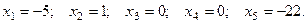
Сделаем проверку:

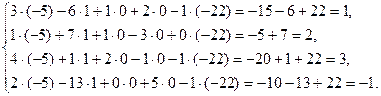
Получили тождественное равенство. Аналогичным образом можно получить любое другое частное решение, например, при 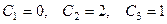получим:

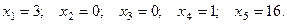
Подставив эти значения переменных в уравнения системы, также получим верные равенства.

ОДНОРОДНЫЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

Отдельно следует выделить множество однородных уравнений, т.е. уравнений вида:

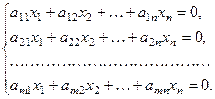
Такие системы всегда совместны, так как всегда имеется тривиальное (т.е. нулевое решение ).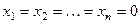

Нулевое решение будет единственным, если ранг основной матрицы системы равен числу неизвестных, т.е. в случае 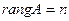. Если же 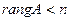, то система имеет бесконечно много решений.

Рассмотрим примеры: найти фундаментальные системы ре -шений однородных систем линейных уравнений

1.

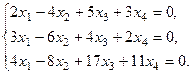
Для однородных систем нет смысла писать расширенную мат- рицу, так как элементарные преобразования не меняют нули, стоящие в правых частях системы уравнений. Поэтому про -изводим преобразования основной матрицы системы:

˜

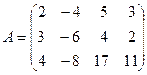Вторую строку умножим на (-1) и прибавим к первой и тре -тьей строке, получим:

˜ ˜

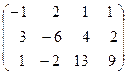С помощью первой строки получим нули в первом столбце, для чего умножим её на (3) и прибавим к второй строке и просто прибавим к третьей строке:

˜ ˜

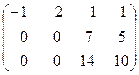Умножим вторую строку на (-2) и прибавим к третьей:

˜ .

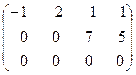Итак, 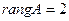, т.е в решении данной системы 2 базисные переменные и две свободные. Запишем полученную систему:

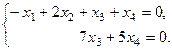
Из второго уравнения: 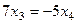, чтобы упростить вычисле –ния, удобно положить 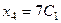, тогда 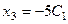. Тогда пер -вое уравнение принимает вид: 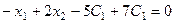. Необходимо ввести ещё одну свободную переменную, напри – мер 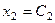. Тогда 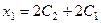. В этом случае, общее решение имеет вид:

.

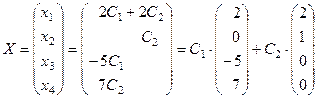Каждый из векторов:

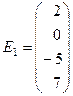и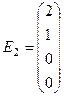

является решением системы. В самом деле, для вектора :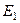

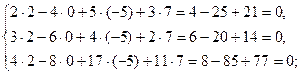для вектора :

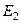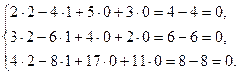и любая комбинация этих решений также является решением системы, т.е. общее решение исходной однородной системы имеет вид: 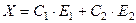, а сами векторы 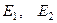об- разуют фундаментальную систему решений данной однород- ной системы линейных уравнений.

2.

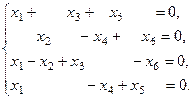
Запишем её матрицу:

˜

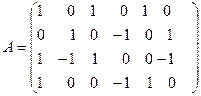Умножим первую строку на (-1) и прибавим к третьей и четвёртой строке:

˜ ˜

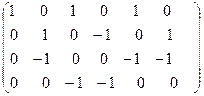Вторую строку прибавим к третьей:

˜ ˜

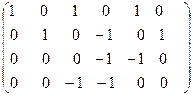Поменяем местами третью и четвёртую строки:

˜ .

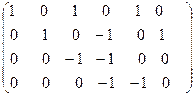Все элементы ниже главной диагонали равны нулю. Поэтому 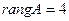. Неизвестных 6. Поэтому решение системы имеет 4 базисных переменных и 2 свободные. Запишем полученную систему:

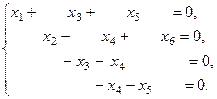
Выберем в качестве свободных переменных 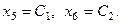Тогда из четвёртого уравнения 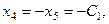так как из тре -тьего уравнения 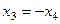, то 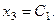Из второго уравнения

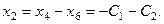Из первого уравнения:

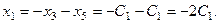
Тогда общее решение имеет вид:

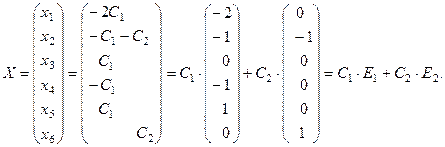
Векторы 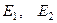образуют фундаментальную систему реше-ний. Проверьте самостоятельно, что каждый из этих векторов является решением системы. 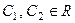, т.е. произвольные постоянные.