Теорема Гаусса. Найдем поток вектора электрического поля точечного заряда q через произвольную замкнутую поверхность S
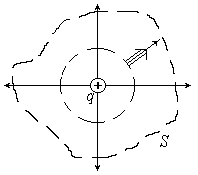 |
Найдем поток вектора 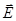 электрического поля точечного заряда q через произвольную замкнутую поверхность S, охватывающую данный заряд. Для этого проведем поверхность сферы с центром в точке расположения заряда внутри выбранной поверхности S. Число силовых линий, пронизывающих поверхности S и сферы одно и тоже тогда
электрического поля точечного заряда q через произвольную замкнутую поверхность S, охватывающую данный заряд. Для этого проведем поверхность сферы с центром в точке расположения заряда внутри выбранной поверхности S. Число силовых линий, пронизывающих поверхности S и сферы одно и тоже тогда 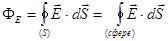 .
.
Во всех точках поверхности сферы единичный вектор нормали 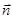 и вектор
и вектор 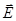 сонаправлены, а по модулю
сонаправлены, а по модулю 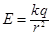 принимает одинаковое значение. В этом случае
принимает одинаковое значение. В этом случае 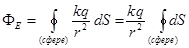 , где
, где 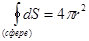 есть площадь поверхности сферы, т.е.
есть площадь поверхности сферы, т.е. 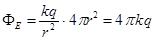 . Учитывая, что в системе СИ
. Учитывая, что в системе СИ 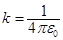 получим
получим 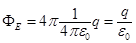 .
.
Поток вектора напряжённости электрического поля через замкнутую поверхность S равен заряду q, находящемуся внутри этой поверхности делённому на электрическую постоянную 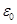 . Положительный заряд создаёт положительный поток (силовые линии поля выходят из поверхности), отрицательный заряд создаёт отрицательный поток (силовые линии поля будут входить внутрь поверхности).
. Положительный заряд создаёт положительный поток (силовые линии поля выходят из поверхности), отрицательный заряд создаёт отрицательный поток (силовые линии поля будут входить внутрь поверхности).
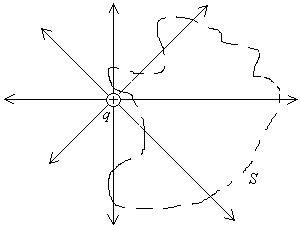 Рис. 2. Рис. 2. |
Рассмотрим случай, когда заряд q, создающий поле находится за пределами замкнутой поверхности S. Как видно из рис.2, число силовых линий входящих внутрь поверхности (создающих отрицательный поток) равно числу линий выходящих из поверхности (создающих положительный поток), т.е. общий поток вектора напряженности через замкнутую поверхность S будет равен нулю: 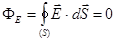 .
.
Рассмотрим поле, созданное системой точечных зарядов q1, q2, q3, q4, q5. (см. рис. 3.). По принципу суперпозиции полей 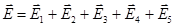 , следовательно
, следовательно
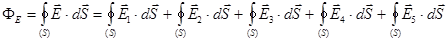 .
.
Заряды q2 и q4 находятся за пределами замкнутой поверхности S, а заряды q1, q3 и q5 внутри этой поверхности, т.е.
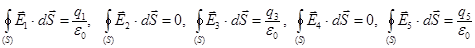 тогда
тогда 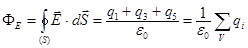 .
.
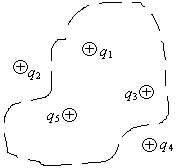 Рис. 3. Рис. 3. |
Таким образом, мы пришли к формулировке теоремы Гаусса: Поток вектора напряжённости электрического поля через любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри объёма ограниченного этой поверхностью делённой на электрическую постоянную 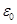 :
: 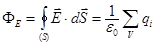
При непрерывном распределении заряда вводят понятие плотности зарядов: объемной плотности заряда 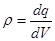 — заряд приходящийся на единицу объема, поверхностной плотности заряда
— заряд приходящийся на единицу объема, поверхностной плотности заряда 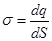 — заряд приходящийся на единицу площади, линейной плотности заряда
— заряд приходящийся на единицу площади, линейной плотности заряда 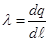 — заряд приходящийся на единицу длинны. В этом случае теорема Гаусса принимает вид:
— заряд приходящийся на единицу длинны. В этом случае теорема Гаусса принимает вид: 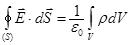 , (1)
, (1)
где 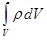 — есть заряд, находящийся внутри объёма, ограниченного поверхностью S.
— есть заряд, находящийся внутри объёма, ограниченного поверхностью S.
Теорема Гаусса является интегральной формулировкой закона Кулона, т.к. справедливость её возможна только при обратно пропорциональной зависимости напряжённости поля точечного заряда от квадрата расстояния от заряда до точки поля.
