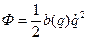Уравнения Лагранжа II рода описывают не только механические движения но и, нередко, движения немеханической природы

Вычисление Т, П и Ф в обобщённых координатах

Пусть система состоит из «n» точек и имеет «s» степеней свободы.

Кинетическая энергия системы:

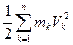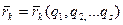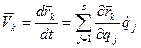T= , так как но , тогда кинетическая энергия будет равна: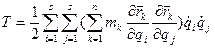

назовём в этой формуле множитель в скобках: 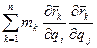= 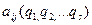коэффициентом инерции.Тогда уравнение кинетической энергии примет вид:

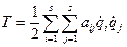при s=1 получим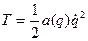

Рассмотрим потенциальную энергию системы:

П=П(q_1, q_2, …q_s)разложим её в ряд Маклорена:

П=П(q_1, q_2, …q_s)=П(0, 0, …0) +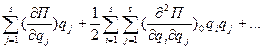

Принимаем П(0, 0, …0)=0, тогда 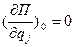выражает состояние равновесия.

П=П(q_1, q_2, …q_s)= 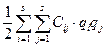где C_ij= 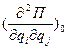коэффициент жёсткости

Потенциальная энергия П= 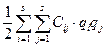, При s=1 П=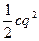

Функция рассеивания энергии (функция Релея)

Рассмотрим случай, когда сила сопротивления среды, что воздействует на к-тую точку системы, равна .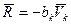

Тогда обобщённая сила сопротивления, соответствующая 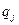обобщённой координате, будет равна:

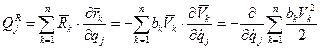
где 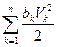=Ф – функция рассеивания или функция Релея.

Структура Ф (функции рассеивания) такая же как у Т (кинетической энергии), а потому 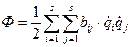, где 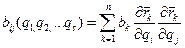, если s=1 то