Двійкові sm на два і три входи
Суматорами називаються дискретні пристрої комп’ютера, які здійснюють арифметичне додавання двох n - розрядних чисел, поданих у вигляді двійкових кодів.
Суматори являються ядром схем арифметико-логічних пристроїв (АЛП), за допомогою яких реалізується ряд різних операцій і вони є частиною усіх процесорів.
Апаратна складність та швидкодія являється дуже важливими параметрами і тому розроблено багато варіантів суматорів.
Термін «суматор» охоплює широкий спектр пристроїв, починаючи з найпростіших логічних схем і закінчуючи складними цифровими вузлами.
Суматори широко застосовуються в дискретних системах вибірки інформації при побудові арифметичних і керуючих пристроїв. Їх використання дозволяє виконувати як операцію додавання так і інші арифметичні операції за рахунок різного подання кодів чисел.
Класифікацію суматорів можна виконувати за різними ознаками, рис.1:
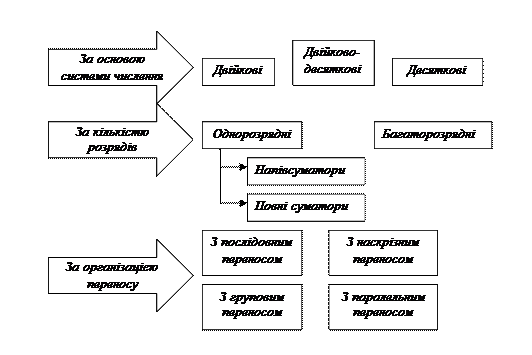
Рис.1. Класифікація комбінаційних суматорів
Ø способом додавання – паралельні, послідовні та паралельно-послідовні;
Ø організацією зберігання результату додавання – комбінаційні, накопичувальні, комбіновані;
Ø розрядністю операндів – 8-, 16-, 32-, 64 розрядні;
Ø часом додавання – синхронні, асинхронні.
УГП однорозрядного суматора та таблиця істинності його роботи представлена на рис.2
| ві | аі | Рі | Si | Pi+1 |
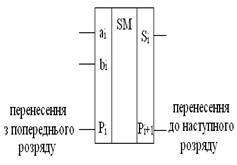
Рис.2.
Задача 1. Є два числа А=510 та В=610. Знайти суму цих чисел, використовуючи таблицю істинності рис.1. Записати двійкове значення Рі, Si та Pi+1, та побудувати схему “n”- розрядного суматора за допомогою одно розрядного суматора.
На практиці зручніше використовувати не одно розрядний, а багато розрядний суматор. На рис. 3. наведено приклад реальної ІМС для суматора – К555ИМ6 – чотирьох розрядний двійковий суматор з прискореним переносом.
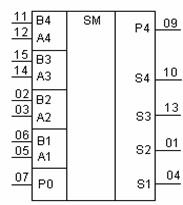 Рис.3. УГП ІМС К555ИМ6 Рис.3. УГП ІМС К555ИМ6 | |
| Таблиця призначення виводів | |
| № виводу | Призначення |
| 02, 03, 05, 06, 11, 12, 14, 15 | – входи інформаційні; |
| – вхід переносу; | |
| – вихід прискореного переносу; | |
| 01, 04, 10, 13 | – виходи; |
| – загальний; | |
| - напруга живлення (Uживл) | |
В цифровій техніці операція додавання використовується і для реалізації віднімання. Це стає можливим за рахунок використання прямих, обернених та додаткових кодів.
Для чисел, що мають однаковий знак додавання відбувається за модулями, і знак залишається тим же.
Для чисел з різними знаками цей процес стає трохи складнішим. Розглянемо на прикладі, як можна виконати операцію віднімання використовуючи суматор (ІС К555ИМ3) та логічний елемент по mod2 (К555ЛП5)для чисел, що можуть мати різні знаки.
Задача 2. Є два числа: А = 310, В = -210. На рис.4 представлена схема сумматора для чисел А=0.0112 та В=1.0102. Так як число А є додатнім, то додатковий код співпадає з прямим його кодом, а число В –від’ємне, його потрібно перетворити у додатковий код*.
Апр.код=0.0112 Впр.код=1.0102 Ад.код=0.0112 Вд.код=1.1102
________________________________________________________________
* Впр.код=1.010; Воб.код=1.101, Вд.код=1.101+1=1.110
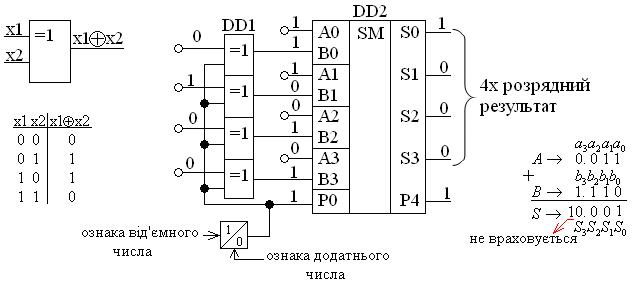
Рис. 4.
