Следствия из свойств определителей

Определители. Основные сведения

Определение.Определитель (детерминант) матрицы 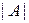– это число, характеризующее квадратную матрицу и вычисляемое по специальному правилу:

1. Определитель первого порядка (n = 1)

.

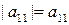2. Определитель второго порядка (n = 2)

.

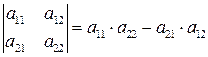3. Определитель третьего порядка n = 3

=

=а₁₁а₂₂а₃₃ +а₁₂а₂₃a₃₁ + а₂₁а₃₂a₁₃ - a₃₁a₂₂a₁₃ - a₁₂a₂₁a₃₃ - a₃₂a₂₃a₁₁.

Определители более высокого порядка вычисляются рекурентно (см. ниже).

Определитель матрицы А обозначается также detA или символом D.

Определение. Минором 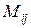– элемента 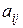– называется определитель -го порядка, полученный вычеркиванием i-й строки и j-го столбца.

Определение.Величина называется алгебраическим дополнением элемента .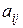

Примечание.

· Определитель n-го порядка имеет n² миноров -го порядка.

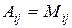· , если 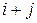– четное число;

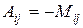· , если 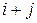– нечетное число.

Основные свойства определителей

1.Равноправие строк и столбцов.

,

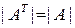то есть определитель транспонированной матрицы равен определителю исходной матрицы.

Замечание.Все свойства, сформулированные для строк, верны и для столбцов.

В частности, при 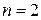имеем:

2.Правило Лапласа, разложения по строке.

Для любой строки, напрмер 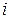-той, справедливо равенство:

,

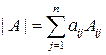то есть определитель равен сумме произведений элементов 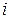-той строки на их алгебраические дополнения.

Пример. Вычислить определитель третьего порядка разложением по строке:

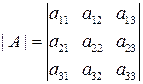= , где i = 1, 2, 3.

3.Свойство нормировки.

Определитель единичной матрицы равен 1.

4.Аддитивность.

Если все элементы какой-либо строки определителя представляют сумму двух слагаемых, то определитель равен сумме двух соответствующих определителей:

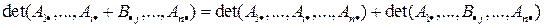
В частности, при 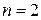имеем:

.

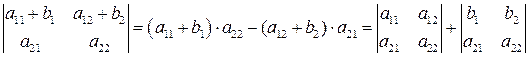5.Однородность.

Общий множитель какой-либо строки можно выносить за знак определителя:

В частности, при 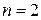имеем:

.

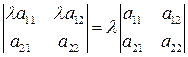Пример. .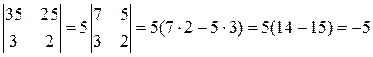

6.Антисимметричность.

При перестановке любых двух строк, определитель меняет знак.

.

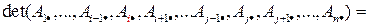
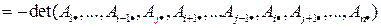В частности, при 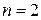имеем:

.

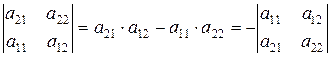7.Определитель произведения двух квадратных матриц равен произведению их определителей:

.

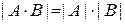Следствия из свойств определителей

1.Определитель диагональной матрицы равен поизведению диагональных элементов.

Пример. .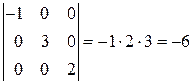

2.Определитель треугольной матрицы равен поизведению диагональных элементов.

Пример. .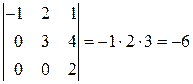

3.Если в определителе есть две одинаковые строки, то он равен нулю.

Доказательство.

Пусть в матрице 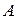строк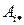и и 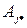- одинаковые (по условию) то есть

( ). (*)

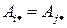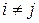Обозначим определитель матрицы 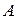через 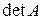. Переставим местами строки с номерам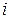и и 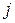. С одной стороны, по условию теоремы, они одинаковые, а значит от их перестановки ничего не изменится. С другой стороны, по свойству 6, при перестановки любых двух строк определитель меняет знак, а значит он равен нулю.

4.Определитель не изменится, если к элементам какой-либо строки прибавить элементы другой строки, предварительно умноженные на одно и то же число.

.

В частности, при 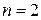имеем:

.

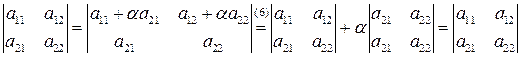Доказательство.

Обозначим 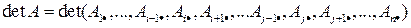. Прибавим к 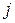-той строке определителя 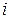-тую строку , домноженную на число 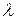: 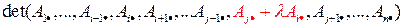. По свойству аддитивности и однородности имеем: =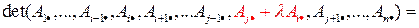

= .

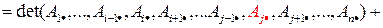
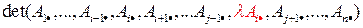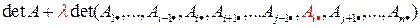Последнее слагаемое равно нулю, так как представляет собой определитель с двумя одинаковыми строками.

Пример. .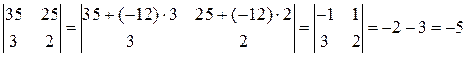

5.Определитель не изменится, если к элементам какой-либо строки прибавить линейную комбинацию других строк.

Замечание. Следсвие 5 является обобщением следствия 4. Докажите самостоятельно.

6.Определитель равен нулю, если все элементы какого-либо его ряда равны нулю:

.

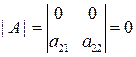7.Сумма произведений элеменов некоторой строки на алгебраические дополнения другой строки равна нулю, то есть

, .

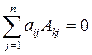8.Определитель некоторой матрицы равен нулю, тогда и только тогда, когда строки этой матрицы линейно зависимы.

1) Если строки линейно зависимы, то существует строка являющаяся линейной комбинацией остальных строк. Прибавим к ней эту комбинацию с противоположым знаком.при этом значение определителя согласно свойству 11 не изменится. Но, таким образом, получим нулевую строку. А, согласно свойству 13, определитель равен нулю.

2) Предположим противное. Определитель матрицы равен нулю, а ее строки – линейно независимы. Но по определению Л.Н. строк следует, что их линейная комбинация с ненулевым набором коэффициентов никогда не равна нулю