Определение соответствия распределения случайных возмущений нормальному закону распределения

Непрерывная случайная величина Х называется распределенной по нормальному закону с параметрами μ и σ, если ее плотность распределения есть

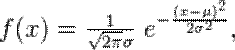
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Закон распределения для случайного возмущения принимает вид:

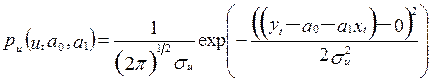Если случайное возмущение подчиняется нормальному закону распределения, то оценки параметров модели несмещенные и эффективные.

Основные числовые характеристики вектора остатков в классической множественной регрессионной модели.

Классическая линейная модель множественной регрессии (КЛММР) представляет собой простейшую версию конкретизации требований к общему виду функции регрессии f(X), природе объясняющих переменных X и статистических регрессионных остатков e(Х) в общих уравнениях регрессионной связи. В рамках КЛММР эти требования формулируются следующим образом:

Из (2.5) следует, что в рамках КЛММР рассматриваются только линейные функции регрессии, т.е.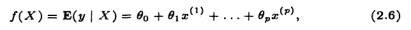

В повторяющихся выборочных наблюдениях (xi(1), xi(2),..., хi(p); yi) единственным источником случайных возмущений значений yi являются случайные возмущения регрессионных остатков ei.

Кроме того, постулируется взаимная некоррелированность случайных регрессионных остатков (E(eiej) = 0 для i ¹ j). Это требование к регрессионным остаткам e1,...,en относится к основным предположениям классической модели и оказывается вполне естественным в широком классе реальных ситуаций. Тот факт, что для всех остатков e1,e2,...,en выполняется соотношение Eei2; =s2 , где величина s2 от номера наблюдения i не зависит, означает неизменность дисперсий регрессионных остатков. Последнее свойство принято называть гомоскедастичностью регрессионных остатков.

Сумма квадратов остатков (RSS) измеряет необъясненную часть вариации зависимых переменных. Она используется как основная минимизируемая величина в методе наименьших квадратов и для расчета других показателей.

Стандартная ошибка регрессии (SEE) измеряет величину квадрата (ошибки), приходящейся на одну степень свободы модели.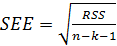

Она используется в качестве основной величины для измерения качества оценивания модели (чем она меньше, тем лучше).