Формулы дифференцирования
Н.П. Зубарева
Высшая математика
Методическое пособие по изучению темы
"Производная функции и ее применение"
Калининград, 2008
ББК 22.1
Составитель: Н.П. Зубарева, канд. пед. наук, доцент.
Рецензент: А.М. Карлов, доктор техн. наук, профессор.
Методическое пособие предназначено студентам для изучения принципов дифференцирования функций. Подробно пояснено решение отдельных заданий. Для самостоятельного решения предложен ряд заданий, ответы на которые есть на с. 23. В пособии имеется справочный материал.
Печатается по решению Ученого совета БИЭФ, протокол №6 от 03 июля 2008 г.
Oacute; БИЭФ, 2008.
Oacute; Зубарева Н.П., 2008.
Содержание
Формулы дифференцирования. 4
Действия со степенями.. 5
Уравнение касательной и нормали к кривой.. 12
Механический смысл производной.. 13
Приращение функции. Дифференциал функции.. 14
Исследование функций и построение графиков. 16
Ответы.. 23
Формулы дифференцирования
I. 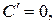 С – постоянная. II.
С – постоянная. II. 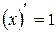 .
.
III. 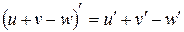 . IV.
. IV. 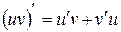 .
.
V. 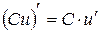 , С – постоянная. VI.
, С – постоянная. VI. 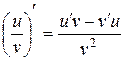 .
.
VII. 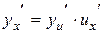 .
.
Основные элементарные Сложные функции
функции
VIII. 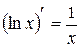 , 8.
, 8. 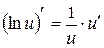
IX. 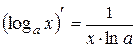 , 9.
, 9. 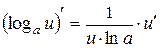 .
.
X. 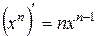 , 10.
, 10. 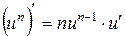 .
.
XI. 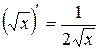 , 11.
, 11. 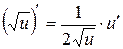 .
.
XII. 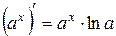 , 12.
, 12. 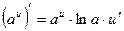 .
.
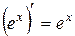 , 13.
, 13. 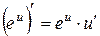 .
.
XIII. 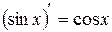 , 14.
, 14. 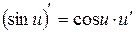 .
.
XIV. 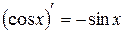 , 15.
, 15. 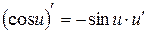 .
.
XV. 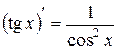 , 16.
, 16. 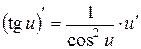 .
.
XVI. 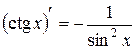 , 17.
, 17. 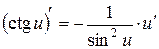 .
.
XVII. 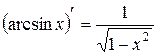 , 18.
, 18. 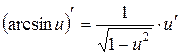 .
.
XVIII. 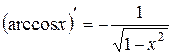 , 19.
, 19. 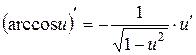 .
.
XIX. 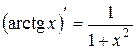 , 20.
, 20. 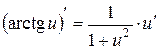 .
.
XX. 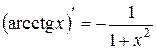 , 21.
, 21. 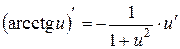 .
.
Задание 1.Найти производную функции 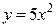 .
.
Решение: 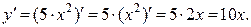
Функция 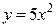 равна произведению постоянной величины 5 и переменной х2. По формуле V выносим постоянную величину перед производной, затем по формуле Х находим производную х2.
равна произведению постоянной величины 5 и переменной х2. По формуле V выносим постоянную величину перед производной, затем по формуле Х находим производную х2.
Задание 2. Найти производную функции 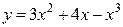 .
.
Решение:
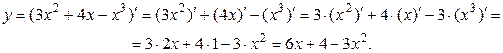
Использовали формулы III, V, II, X.
Найти самостоятельно производную функции:
1а) 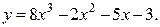
1б) 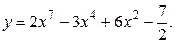
Для вычисления производных полезно сначала преобразовать выражение.
Напомним некоторые формулы действий со степенями.
