Задача с потенциалом в виде двойной ямы
Модель вынужденных колебаний изогнутого стержня была построена Холмсом на основе уравнения типа Дуффинга. С помощью аналогового моделирования им доказана возможность хаотических колебаний этой системы. В безразмерном виде полученное, Холмсом уравнение таково:
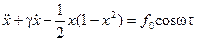 ,
,
где 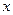 – поперечное смещение стержня, который описывается простой одномодовой моделью.
– поперечное смещение стержня, который описывается простой одномодовой моделью.
Это уравнение может также служить моделью частицы в потенциале из двух ям. Эта модель использовалась и при исследовании плазменных колебаний. На рисунке показано отображение Пуанкаре соответствующего странного аттрактора.
К этим примерам близка задача о провале арки с шарниром, вызванном колебаниями (рисунок 1.77).
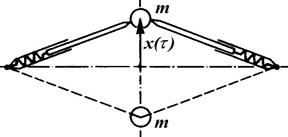
Рисунок 1.77 - Схема арки с шарниром. Вынужденные колебания, сопровождающиеся провалами арки, могут происходить в хаотическом режиме
Это явление описывается уравнением
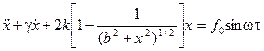 .
.
Если сохранить только кубичные нелинейности, то это уравнение принимает вид, характерный для осциллятора Дуффинга с двумя потенциальными ямами.
