ЛЕКЦИЯ № 20. ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Вопрос 20.1. Производная n-го порядка.

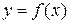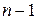Определение 20.1. Пусть дана функция . Производной n‑го порядка от функции называется производная от производной ‑го порядка .

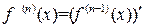Производная второго порядка обозначается

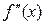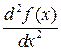или или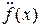

Производная третьего порядка обозначается

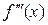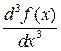или или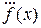

Точками порядок производной принято указывать в теоретической механике. Производные более высоких порядков обозначают, указывая порядок или арабскими или римскими числами

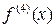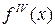, или .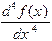

Пример 20.1. Вычислить производную второго порядка от .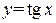

Конец примера.

Для производной n-го порядка справедливы формулы

1) ,

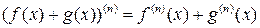2) ,

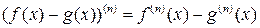3) ,

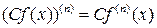4) формула Лейбница ,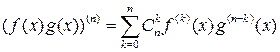

где

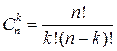‑ биномиальные коэффициенты, .

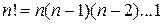Пример 20.2.

,

.

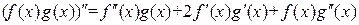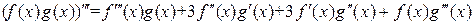Конец прмера.

Вопрос 20.2. Дифференциал n-го порядка.

Определение 20.2. Дифференциалом n-го порядка называется произведение 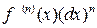и обозначается

.

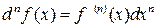Дифференциал n-го порядка обладает следующими свойствами:

1)

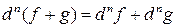
2)

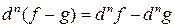
3)

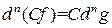
4)

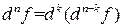
5) формула Лейбница ,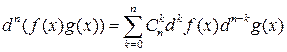

где

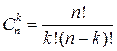‑ биномиальные коэффициенты, .

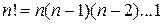Доказательство. Свойства 1) ‑ 3) и 5) есть следствия соответствующих свойств n-й производной. Докажем теперь 4‑е свойство. Пусть x ‑ независимая переменная. Тогда

.

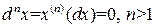Далее, так как 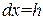, то 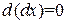, и, следовательно, 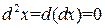, поэтому 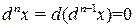. Тогда последовательно получаем

,

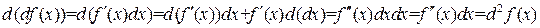то есть 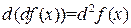. Аналогично

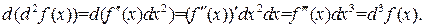
Продолжая, получим

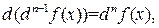
откуда следует

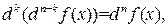
Пример 20.3. Вычислить 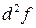от .

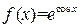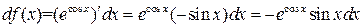
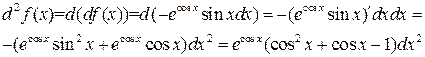
Конец примера.

Вопрос 20.3. Теорема Ферма и Ролля.

Определение 20.2. Точка a называется точкой локального минимума функции , если существует окрестность точки a, такая, что для всех x из этой окрестности справедливо неравенство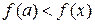

Определение 20.3. Точка a называется точкой локального максимума функции , если существует окрестность точки a, такая, что для всех x из этой окрестности справедливо неравенство .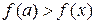

Определение 20.4. Точка а называется точкой локального экстремума функции , если она является или точкой локального минимума, или точкой локального максимума.

Теорема 20.2. (Ферма). Если в точке a имеет локальный экстремум и дифференцируема в этой точке, то (см. рис. 1) .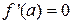

Доказательство. Пусть a есть точка локального минимума. Тогда для достаточно малых h 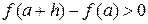. Односторонние производные в точке a равны

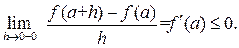
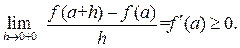
Отсюда следует равенство .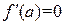

Конец доказательства.

Теорема 20.3. (Ролля). Пусть 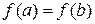и функция непрерывна на отрезке [a,b] и дифференцируема на интервале (a,b). Тогда обязательно найдется точка c, такая, что a<c<b и .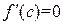

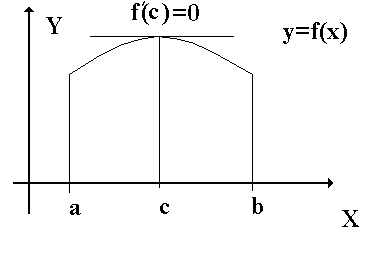
Рис. 1. К доказательству теорем Ферма и Ролля.

Доказательство. Из непрерывности функции на отрезке 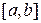следует существование точек 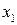и 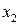этого отрезка, в которых функция принимает максимальное и минимальное значения M и m (пусть для определенност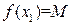и и 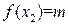). Если M=m, то 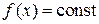и 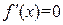для всех x из отрезка 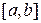. Для этого случая теорема доказана. Если 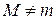, то и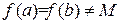ли , или 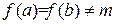. Тогда внутри отрезка 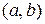существует точка локального экстремума c, в которой по теореме Ферма .

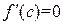Конец доказательства.

Теорема 20.4 (Коши). Пусть функции и 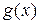непрерывны на отрезке [a,b] и дифференцируемы внутри этого отрезка. Тогда существует точка c такая, что a<c<b и

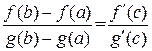
Доказательство. Введем вспомогательную функцию

,

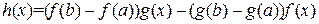тогда

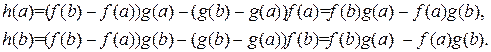
То есть 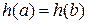. Применяя к функции 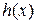теорему Ролля (проверьте условия ее применимости), получим

.

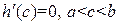Откуда

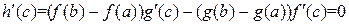
или

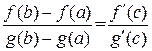
Конец доказательства.