Затухающие одномерные колебания

Если собственные частоты системы существенно меньше частот процессов диссипации, то можно обойтись только механикой (без термодинамики). Когда колебания малы, то функцию среды можно записать в квадратичном виде, например: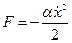

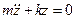(свободное колебание)

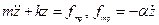
здесь .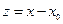

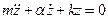
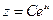
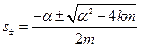
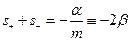
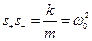
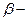показатель затухания

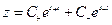
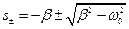
1. 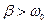-апериодический процесс – колебаний нет

2.

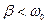
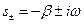, где

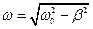
тогда

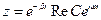
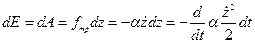
тогда 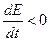, т.е. энергия расходуется на трение.

т.е. для поддержания колебаний необходим приток энергии извне.

Рассмотрим аналогичную задачу для степеней свободы:

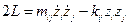
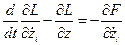
слагаемое в правой части означает воздействие внешней силы.

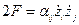-диссипативная функция.

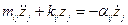
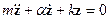
решение ищется в виде 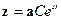, тогда:

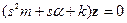
умножим на комплексно-сопряженное:

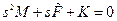
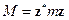
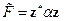
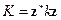
В силу симметрии эти числа вещественны:

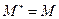
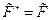
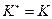
Вводятся обозначения:

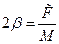и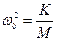

Элементы тензорного анализа в классической механике.

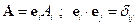
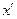Введём координаты и 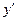, которые повернуты относительно 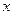и 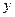на угол .

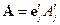
здесь не зависит от выбора координат.

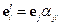
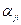- это матрица перехода (в нашем случае матрица поворота).

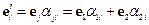
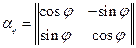
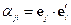
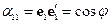
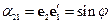
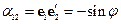
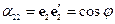
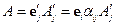
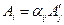
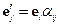
Тензор представим в виде матрицы, а матрица не представима в виде тензора. Рассмотрим свойства матрицы :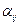

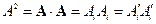
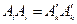
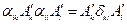
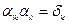- сумма по индексу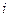

,

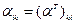
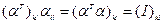где 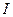- единичная матрица

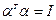
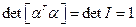
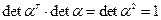
Тогда:

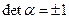
Если 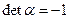, то это соответствует 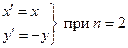и .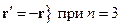

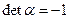-инверсия

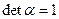- вращение

,

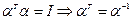
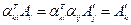
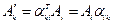
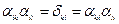
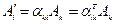
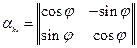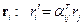
при :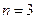

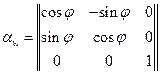
-компонента вектора (тензора первого ранга)

Можно ввести некоторые объекты 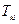, где компонент будет 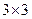, которые преобразуются по правилу:

,

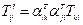где 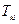- тензор

Для криволинейных координат вводятся контравариантные векторы 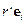и ковариантные векторы .

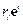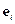и 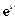- различные системы векторов

,

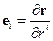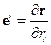
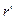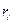здесь и - различные величины.

Оператор .

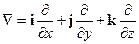
Оператор набла – векторный дифференциальный оператор. Оператор набла можно ввести по-другому:

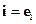
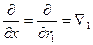
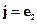
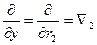
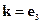
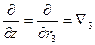
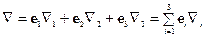
Часто знак суммы опускают (правило суммирования Эйнштейна).

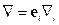
Запишем условие ортонормированности рассматриваемого базиса:

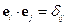
Действия оператора набла:

1. Оператор набла действует на скалярную функцию F:

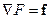или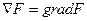

2. Оператор набла скалярно действует на векторную функцию :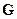

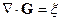
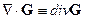
3. Оператор набла векторно умножается на векторную функцию :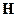

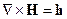
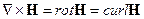
Кроме векторного и скалярного, есть ещё смешенное произведение векторов:

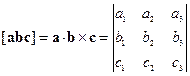- объем параллелепипеда.

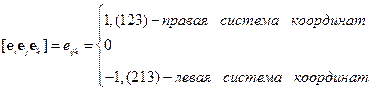
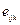- единичный антисимметричный тензор третьего ранга.

Задачи

1. Вычислить градиент функции f(r), зависящей только от модуля радиус-вектора r.

Решение.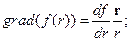

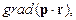
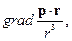
2. Вычислить 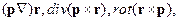где p – постоянный вектор.

Решение.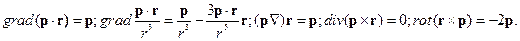

Уравнения Максвелла для электромагнитного поля в вакууме.

Будем использовать гауссову систему единиц.

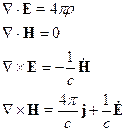
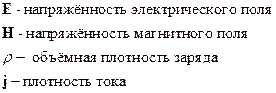
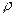и 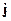являются источниками поля. Уравнения Максвелла позволяют по заданным источникам рассчитать электромагнитное поле. Уравнениям Максвелла в дифференциальной форме ставятся в соответствие уравнения в интегральной форме.