Даны вершины треугольника .
Требуется сделать чертёж и найти:
а)длину стороны  ;б)уравнение стороны
;б)уравнение стороны ;
;
В)длину высоты ; г)площадь треугольника .
31.  . 32.
. 32. 
33.  34.
34. 
35.  36.
36. 
37.  38.
38. 
39.  40.
40. 
Раздел II. Введение в анализ. Дифференциальное исчисление.
41 – 50.Для указанной функции  требуется:
требуется:
а) найтиестественную область определения функции;
б) установить чётность (нечётность) функции.
41. а)  б)
б) 
42. а)  б)
б) 
43. а)  б)
б) 
44. а)  б)
б) 
45. а)  б)
б) 
46. а)  б)
б) 
47. а)  б)
б) 
48. а)  б)
б) 
49. а)  б)
б) 
50.  б)
б) 
Для указанной функции найтиточки разрыва функции и исследовать их характер.Построить график функции.
51.  52.
52.  53.
53. 
54.  55.
55.  56.
56. 
57.  58.
58. 
59.  60.
60. 
61-70.Найти производную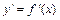 :
:
61. а)  б)
б)  в)
в)  г)
г) 
62. а)  б)
б)  в)
в)  г)
г) 
63. а)  б)
б)  в)
в)  г)
г) 
64. а)  б)
б)  в)
в)  г)
г) 
65. а)  б)
б)  в)
в)  г)
г) 
66. а)  б)
б)  в)
в)  г)
г) 
67. а)  б)
б)  в)
в)  г)
г) 
68. а)  б)
б)  в)
в)  г)
г) 
69. а)  б)
б)  в)
в)  г)
г) 
70. а)  б)
б)  в)
в)  г)
г) 
71-80.Вычислить пределы:
71. а)  б)
б)  в)
в) 
72. а)  б)
б)  в)
в) 
73. а)  б)
б)  в)
в) 
74. а)  б)
б)  в)
в) 
75. а)  б)
б)  в)
в) 
76. а)  б)
б)  в)
в) 
77. а)  б)
б)  в)
в) 
78. а)  б)
б)  в)
в) 
79. а)  б)
б)  в)
в) 
80. а)  б)
б)  в)
в) 
81-90. Для указанной функции  требуется:
требуется:
а) найти наибольшее и наименьшее значения функции на отрезке  ;
;
б) составить уравнение касательной к графику функции в точке  ;
;
в) провести полное исследование непериодической функции и построить её график.
81.  ,
,  .
.
82.  ,
, 
83.  ,
, 
84.  ,
, 
85.  ,
, 
86.  ,
, 
87.  ,
, 
88.  ,
, 
89.  ,
, 
90.  ,
, 
91 – 100.Для указанной функции 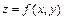 требуется:
требуется:
а)найти дифференциал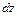 и
и 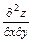 ; б)найти локальные экстремумы.
; б)найти локальные экстремумы.
91. а)  , б)
, б) 
92. а)  б)
б) 
93. а)  б)
б) 
94. а)  б)
б) 
95. а)  б)
б) 
96. а)  б)
б) 
97. а)  б)
б) 
98. а)  б)
б) 
99. а)  б)
б) 
100. а)  б)
б) 
Раздел III. Интегральное исчисление.
101-110.Найти неопределённые интегралы:a)непосредственным интегрированием; б) заменой переменной интегрирования; в) интегрированием по частям.
101. а)  б)
б)  в)
в) 
102. а)  б)
б)  в)
в) 
103. а)  б)
б)  в)
в) 
104. а)  б)
б)  в)
в) 
105. а)  б)
б)  в)
в) 
106. а)  б)
б)  в)
в) 
107. а)  б)
б)  в)
в) 
108. а)  б)
б)  в)
в) 
109. а)  б)
б)  в)
в) 
110. а)  б)
б)  в)
в) 
111-120.Требуется вычислить:
а) определённый интеграл;
б) несобственный интеграл I-ого рода (или установить его расходимость).
111. а)  б)
б)  112. а)
112. а)  б)
б) 
113. а)  б)
б)  114. а)
114. а)  б)
б) 
115. a)  б)
б)  116. а)
116. а)  б)
б) 
117. а)  б)
б)  118. а)
118. а)  б)
б) 
119 а)  б)
б)  120. а)
120. а)  б)
б) 
121-130.Вычислитьплощадь фигуры, ограниченной графиками указанных функций:
121.  ,
,  122.
122.  ,
, 
123.  ,
,  124.
124.  ,
, 
125.  ,
,  126.
126.  ,
, 
127.  ,
,  128.
128.  ,
, 
129.  ,
,  130.
130.  ,
,  ,
, 
Раздел IV. Дифференциальные уравнения.
131-140.Установить тип ДУ первого порядка и найти:
а) общее решение ДУ; б) общее и частное решения ДУ.
А) б) , .
А) б) , .
А) б) , .
А) б) , .
А) б) , .
А) б) , .
А) б) , .
А) б) , .
А) б) , .
А) б) , .
141-150.Требуется найти:
а)общеерешениепростейшего ДУ 2-ого порядка 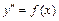 ;
;
б)общее и частное решения однородного линейного ДУ 2-ого порядка с постоянными коэффициентами;
в) общее решение линейного ДУ 2-ого порядка с постоянными коэффициентами и правой частью специального вида.
141. а)  б)
б)  ,
, 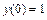 ,
, 
в) 
142. а)  б)
б)  ,
, 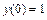 ,
, 
в) 
143. а)  б)
б)  ,
,  ,
, 
в) 
144. а)  б)
б)  ,
, 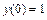 ,
, 
в) 
145. а)  б)
б)  ,
, 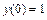 ,
, 
в) 
146. а)  б)
б)  ,
, 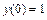 ,
, 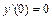
в) 
147. а)  б)
б)  ,
,  ,
, 
в) 
148. а)  б)
б)  ,
,  ,
, 
в) 
149. а)  б)
б)  ,
, 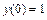 ,
, 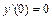
в) 
150. а)  б)
б)  ,
,  ,
, 
в) 
Раздел V. Теория вероятностей и математическая статистика.
151-160. Требуется найти вероятности указанных событий, используя
классическое определение вероятности:
151. а)Бросаются два игральных кубика. Найти вероятность того, что число выпавших очков на одном из кубиков в два раза больше, чем на другом.
б)В магазине выставлены для продажи  изделий, среди которых
изделий, среди которых  изделий некачественные. Найти вероятность того, что взятые случайным образом
изделий некачественные. Найти вероятность того, что взятые случайным образом  изделия будут некачественными.
изделия будут некачественными.
152.а) В первом ящике находятся шары с номерами от 1 до 5, а во втором – с номерами от 6 до 10. Из каждого ящика вынимают по одному шару. Найти вероятность того, что сумма номеров вынутых шаров равна десяти.
б)В партии из  изделий
изделий  изделия имеют скрытый дефект. Найти вероятность того, что из взятых наугад
изделия имеют скрытый дефект. Найти вероятность того, что из взятых наугад  изделий дефектными являются
изделий дефектными являются  изделия.
изделия.
153. а) Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 35. Найти вероятность того, что номер первого наудачу извлеченного жетона содержит цифру 4.
б) На ТЭЦ 15 сменных инженеров, из них 3 женщины. В смену занято 3 человека. Найти вероятность того, что в случайно выбранную смену окажется две женщины.
154.а)Бросаются два игральных кубика. Найти вероятность того, что сумма числа очков на выпавших гранях равна восьми.
б) Из партии, содержащей 10 изделий, среди которых 3 бракованные, наудачу извлекают 3 изделия для контроля. Найти вероятность того, что в выборке содержится одно бракованное изделие.
155.а) В первом ящике находятся шары с номерами от 1 до 5, а во втором – с номерами от 6 до 10. Из каждого ящика вынимают по одному шару. Найти вероятность того, что произведение номеров вынутых шаров больше пятнадцати.
б) В магазине имеются 20 холодильников, причем 15 из них – импортные. Найти вероятность того, что среди 5 проданных в течение дня холодильников окажется три импортных холодильника.
156.а) Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 35. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифру 3.
б) Среди 25 студентов, из которых 15 девушек, разыгрываются 4 билета в театр, причем каждый может выиграть только один билет. Найти вероятность того, что среди обладателей билетов окажутся два юноши и две девушки.
157. а)Бросаются два игральных кубика. Найти вероятность того, что сумма числа очков на выпавших гранях больше четырёх, но меньше семи.
б)В магазине выставлены для продажи  изделий, среди которых
изделий, среди которых  изделий некачественные. Найти вероятность того, что взятые случайным образом
изделий некачественные. Найти вероятность того, что взятые случайным образом  изделия будут некачественными.
изделия будут некачественными.
158. а) В первом ящике находятся шары с номерами от 1 до 5, а во втором – с номерами от 6 до 10. Из каждого ящика вынимают по одному шару. Найти вероятность того, что абсолютная величина разности номеров вынутых шаров равна двум.
б)В партии из  изделий
изделий  изделий имеют скрытый дефект. Найти вероятность того, что из взятых наугад
изделий имеют скрытый дефект. Найти вероятность того, что из взятых наугад  изделий дефектными являются
изделий дефектными являются  изделия.
изделия.
159. а) Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 35. Найти вероятность того, что номер первого наудачу извлеченного жетона является числом, кратным 5 (делится на 5 без остатка).
б) На ТЭЦ 15 сменных инженеров, из них 3 женщины. В смену занято 3 человека. Найти вероятность того, что в случайно выбранную смену окажется хотя бы один мужчина.
160. а)Бросаются два игральных кубика. Найти вероятность того, что сумма числа очков на выпавших гранях меньше их произведения.
б) Среди 25 студентов, из которых 15 девушек, разыгрываются 4 билета в театр, причем каждый может выиграть только один билет. Какова вероятность того, что среди обладателей билетов окажется хотя бы одна девушка.
161-170.Требуется найти вероятности указанных событий, используя:
а) формулы сложения и умножения вероятностей;
б) формулу Бернулли;
161. а)Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом справочнике 0.8, во втором – 0.7, в третьем – 0.85. Найти вероятность того, что формула содержится хотя бы в одном справочнике.
б)Экзамен состоит из 6 вопросов. На каждый вопрос дано четыре возможных ответа, среди которых необходимо выбрать один правильный. Найти вероятность того, что методом простого угадывания удастся ответить не менее чем на 5 вопросов.
162. а)В первом ящике 5 белых и 7 чёрных шаров. Во втором 3 белых и 12 чёрных шаров. Из каждого ящика вынули по шару. Какова вероятность, что оба шара разного цвета.
б)Покупатель приобрел шесть изделий, изготовленных на данном предприятии, 80% изделий которого составляет продукция высшего сорта. Найти вероятность того, что не менее пяти из них являются изделиями высшего сорта.
163. а)Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0.9, для второго – 0.8 и для третьего – 0.85. Найти вероятность того, что в течение некоторого часа два станка из трёх потребуют внимания рабочего.
б)Для нормальной работы автобазы на линии должно быть не менее 8 машин из 10 имеющихся. Вероятность невыхода каждой машины на линию равна 0.1. Найти вероятность того, что автобаза будет работать нормально в ближайший день.
164. а)Три стрелка стреляют по разу в одну мишень независимо друг от друга. Вероятность попадания в цель первым стрелком равна 0.7, вторым – 0.8, третьим – 0.9. Найти вероятность того, что мишень будет поражена два раза.
б)В урне 20 белых и 10 черных шаров. Из урны вынимают подряд 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется три белых.
165. а)Экзаменационный билет по теории вероятностей содержит три вопроса. Вероятности того, что студент ответит на первый и второй вопросы билета равны 0.9; на третий – 0.8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить на все вопросы.
б)Для стрелка, выполняющего упражнение в тире, вероятность попасть в «яблочко» при одном выстреле не зависит от результатов предшествующих выстрелов и равна 0.25. Спортсмен сделал 5 выстрелов. Найти вероятность того, что стрелок попал в «яблочко» не менее четырёх раз.
166. а)Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом справочнике 0.8, во втором – 0.7, в третьем – 0.85. Найти вероятность того, что формула содержится только в одном справочнике.
б)Найтивероятность того, что в семье, имеющей 6 детей, не менее двух девочек. Предполагается, что вероятности рождения мальчика и девочки одинаковые.
167. а)В первом ящике 6 белых и 4 чёрных шара, во втором -7 белых и 3 чёрных. Из каждого ящика наугад вынимают по одному шару. Чему равна вероятность того, что вынутые шары одного цвета.
б)Экзамен состоит из 5 вопросов. На каждый вопрос дано три возможных ответа, среди которых необходимо выбрать один правильный. Найти вероятность того, что методом простого угадывания удастся ответить на все вопросы.
168. а)Рабочий обслуживает три станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0.9, для второго – 0.8 и для третьего – 0.85. Найти вероятность того, что в течение некоторого часа все три станка потребуют внимания рабочего.
б)Покупатель приобрел пять изделий, изготовленных на данном предприятии, 80% изделий которого составляет продукция высшего сорта. Найти вероятность того, что четыре из них являются изделиями высшего сорта.
169. а)Три стрелка стреляют по разу в одну мишень независимо друг от друга. Вероятность попадания в цель первым стрелком равна 0.7, вторым – 0.8, третьим – 0.9. Найти вероятность того, что мишень будет поражена хотя бы один раз.
б)Для нормальной работы автобазы на линии должно быть не менее 9 машин из 10 имеющихся. Вероятность невыхода каждой машины на линию равна 0.2. Найти вероятность того, что автобаза будет работать нормально в ближайший день.
170. а)Экзаменационный билет по теории вероятностей содержит три вопроса. Вероятности того, что студент ответит на первый и второй вопросы билета равны 0.9; на третий – 0.8. Найти вероятность того, что студент сдаст экзамен, если для этого необходимо ответить хотя бы на два вопроса из трёх.
б)Вероятность выиграть по лотерейному билету равна  . Найти вероятность выиграть не менее чем по двум билетам из шести.
. Найти вероятность выиграть не менее чем по двум билетам из шести.
171-180.Составить закон распределения дискретной случайной величины 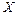 ; построить многоугольник полученного распределения; вычислить её математическое ожидание
; построить многоугольник полученного распределения; вычислить её математическое ожидание  и дисперсию
и дисперсию  .
.
171.В партии из 10 деталей содержится 3 нестандартных. Наудачу отобраны две детали. Дискретная случайная величина Х – число нестандартных деталей среди двух отобранных.
172.Стрелок производит по мишени два выстрела. Вероятность попадания в мишень при каждом выстреле равна 0.9. Дискретная случайная величина Х – число попаданий в мишень.
173.В экзаменационном билете две задачи. Вероятность правильного решения первой задачи равна 0.9, второй – 0.6. Дискретная случайная величина Х – число правильно решённых задач в билете.
174.В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 2 детали. Дискретная случайная величина Х – число нестандартных деталей среди отобранных.
175.Стрелок производит по мишени два выстрела. Вероятность попадания в мишень при каждом выстреле равна 0.7. Дискретная случайная величина Х – число промахов.
176.Из пяти купленных роз 2 красные. Для составления букета наудачу берут 3 розы. Дискретная случайная величина Х – число красных роз среди отобранных.
177.В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 2 детали. Дискретная случайная величина Х – число стандартных деталей среди отобранных.
178.Устройство состоит из двух независимо работающих элементов. Вероятность отказа каждого элемента в одном опыте равна 0.1. Дискретная случайная величина Х – число отказавших элементов в одном опыте.
179.В урне 6 белых и 4 чёрных шаров. Из неё извлекли два шара. Дискретная случайная величина Х – число белых шаров среди отобранных.
180.В урне 6 белых и 4 чёрных шаров. Из неё извлекли два шара. Дискретная случайная величина Х – число чёрных шаров среди отобранных.
181-190.Дляприведённой выборкитребуется:
а)построить вариационный и дискретный статистический ряды;
б) вычислить числовые характеристики выборки:  ,
,  ,
,  (размах),
(размах),  (среднее арифметическое),
(среднее арифметическое),  (дисперсию); в) построить полигон частот.
(дисперсию); в) построить полигон частот.
181.Выборка объема :
:
0 4 2 0 5 1 1 3 0 2 2 4 3 2 3 3 0 4 5 1
182.Выборка объема :
:
4 5 6 4 4 6 2 2 5 4 5 5 4 2 3
183.Выборка объема :
:
2 2 1 3 4 2 1 1 3 3 4 3 2 4 5
184.Выборка объема :
:
9 8 10 6 6 7 9 9 10 4 10 11 11 11 6
185.Выборка объема :
:
5 5 4 2 6 2 1 5 3 3 1 5 6 4 3 3 4 1 5 5
186.Выборка объема :
:
2 1 2 3 1 1 0 2 2 4 3 3 0 3 0 2 3 1 2 2
187.Выборка объема :
:
6 8 9 9 4 9 6 8 9 4 6 6 8 6 4
188.Выборка объема :
:
5 10 10 9 5 8 8 9 6 6 6 8 8 10 8
189.Выборка объема :
:
1 0 2 6 5 4 1 4 5 1 2 4 2 2 2
190.Выборка объема :
:
1 3 3 2 0 2 4 3 2 1 2 2 2 2 3 3 1 1 1 3
191-200.Дляприведённой выборкитребуется:
а) вычислить числовые характеристики группированной выборки:  ,
,  ,
,  (размах),
(размах),  (среднее арифметическое),
(среднее арифметическое),  (дисперсию);
(дисперсию);
б) построить гистограмму частот.
191.Данные о месячной заработной плате 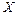 по цеху (в тыс.руб.)
по цеху (в тыс.руб.)
| Зар.плата | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 | 14-16 | 16-18 |
| Число рабочих |
192.Данные о расходе 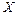 фирм, продающих компьютеры, на рекламу (в % к общему расходу фирмы):
фирм, продающих компьютеры, на рекламу (в % к общему расходу фирмы):
| Расход на рекламу | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| Число фирм |
193. Выборочные данные о стаже работы 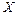 сотрудников банка:
сотрудников банка:
| Стаж, лет | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| Число сотрудников |
194.Данные о годовом товарообороте 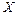 (млн.руб) продовольственных магазинов города:
(млн.руб) продовольственных магазинов города:
| Товарооборот | 10-12 | 12-14 | 14-16 | 16-18 | 18-20 |
| Число магазинов |
195.Данные о месячной заработной плате 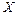 по цеху (в тыс.руб.):
по цеху (в тыс.руб.):
| Зар.плата | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 |
| Число рабочих |
196.Данные измерений роста 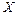 (в см) студентов одного из вузов города:
(в см) студентов одного из вузов города:
| Рост | 150-160 | 160-170 | 170-180 | 180-190 | 190-200 |
| Число студентов |
197.Данные о годовом товарообороте 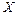 (млн.руб) мебельных магазинов города:
(млн.руб) мебельных магазинов города:
| Товарооборот | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Число магазинов |
198.Данные измерений внутреннего диаметра 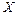 (в мкм) поршневых колец:
(в мкм) поршневых колец:
| Диаметр | 28-32 | 32-36 | 36-40 | 40-44 | 44-48 |
| Число колец |
199.Данные о расходе 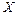 фирм, продающих автомобили, на рекламу (в % к общему расходу фирмы):
фирм, продающих автомобили, на рекламу (в % к общему расходу фирмы):
| Расход на рекламу | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Число фирм |
200.Данные о содержании 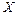 (в куб. м) деловой древесины в одном дереве:
(в куб. м) деловой древесины в одном дереве:
| Содержание деловой древесины | 0.2-0.6 | 0.6-1.0 | 1.0-1.4 | 1.4-1.8 |
| Число деревьев |
Вопросы к экзамену.
Раздел I. «Аналитическая геометрия и линейная алгебра».
1. Понятие матрицы. Частные виды матриц (квадратная, треугольная, диагональная, нулевая, единичная). Элементарные преобразования матриц. Понятие эквивалентности и равенства матриц.
2. Действия над матрицами (сложение, вычитание, умножение матрицы на число, умножение матрицы на матрицу), их свойства.
3. Определители 2-ого и 3-его порядка, их вычисление. Основные свойства определителей.
4. Понятие определителя n-ого порядка. Минор и алгебраическое дополнение элемента определителя. Разложение определителя по элементам строки или столбца.
5. Понятие системы линейных алгебраических уравнений (СЛАУ). Частные виды СЛАУ (квадратная, однородная, неоднородная). Матрица, расширенная матрица, определитель СЛАУ.
6. Решение, множество решений СЛАУ. Совместность, несовместность, определённость, неопределённость, эквивалентность СЛАУ. Элементарные преобразования СЛАУ, их основное свойство.
7. Метод Крамера для решения СЛАУ, условия его применимости.
8. Метод Гаусса решения СЛАУ. Условия несовместности, определённости и неопределённости СЛАУ по методу Гаусса.
9. Понятие обратной матрицы. Вырожденные и невырожденные матрицы. Условие существования обратной матрицы. Основные способы нахождения обратной матрицы.
10. Матричная форма записи СЛАУ. Матричный способ (метод обратной матрицы) решения СЛАУ, условия его применимости.
11. Минор  -ого порядка, базисный минор, ранг матрицы. Критерий совместности систем линейных алгебраических уравнений.
-ого порядка, базисный минор, ранг матрицы. Критерий совместности систем линейных алгебраических уравнений.
12. Понятие геометрического вектора. Равенство векторов. Противоположный вектор. Орт вектора. Коллинеарность и компланарность векторов.
13. Графические правила сложения, вычитания, умножения вектора на число. Проекция вектора на вектор.
14. Понятие декартовой системы координат в  . Радиус-вектор, координаты точки. Вычисление длины вектора; направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.
. Радиус-вектор, координаты точки. Вычисление длины вектора; направляющих косинусов вектора; координат вектора, заданного двумя точками; расстояния между точками.
15. Скалярное произведение геометрических векторов и его свойства. Выражение скалярного произведения через координаты векторов. Вычисление угла между векторами, условие их ортогональности.
16. Векторное произведение векторов, его геометрический смысл и свойства, выражение векторного произведения через координаты векторов. Условие коллинеарности векторов.
17. Смешанное произведение векторов, его геометрический смысл и свойства. Выражение смешанного произведения через координаты векторов. Условие компланарности векторов.
18. Прямая линия на плоскости и её общее уравнение. Нормальный и направляющий векторы прямой. Уравнение прямой, проходящей через точку, перпендикулярно вектору. Построение прямой на плоскости.
19. Каноническое уравнение прямой; уравнения прямой: проходящей через две точки, с угловым коэффициентом, в отрезках. Расстояние от точки до прямой на плоскости. Угол между прямыми на плоскости и его вычисление; условия  и
и  прямых.
прямых.
20. Окружность, эллипс, гипербола, парабола, их канонические уравнения и построение.
Раздел II. Введение в анализ. Дифференциальное исчисление.
21. Понятие множества. Подмножество. Универсальное множество. Способы задания множеств. Операции над множествами (объединение, пересечение, разность, дополнение).
22. Множества чисел. Действительные числа, модуль числа и его свойства. Числовые промежутки. Окрестность точки.
23. Понятие функции. Основные способы задания функции. Естественная область определения функции. Явное, неявное, параметрическое задание функции. График функции.
24. Основные элементы поведения функции (чётность, нечётность, периодичность, ограниченность, монотонность).
25. Основные элементарные функции:  ,
,  ,
,  ,
,  ,
,  ;
;  ,
,  ;
;  ,
,  ;
;  ,
,  ,
,  ,
,  ;
;  ,
,  ,
,  ,
,  . Основные свойства, графики.
. Основные свойства, графики.
26. Простейшие элементарные функции:  ,
,  ;
;  ,
,  , их свойства и графики.
, их свойства и графики.
27. Понятие обратной и сложной функций. Элементарные функции.
28. Функция натурального аргумента. Понятие числовой последовательности. Ограниченные и неограниченные, монотонные последовательности.
29. Понятие предела числовой последовательности, его геометрический смысл. Сходящиеся и расходящиеся последовательности. Признак сходимости монотонной последовательности. Число  .
.
30. Понятие числового ряда (ЧР). Частичная сумма и сумма ряда. Сходящиеся и расходящиеся ряды, их свойства. Геометрический и обобщённый гармонический числовые ряды, условия их сходимости и расходимости.
31. Понятие предела функции в конечной точке и на бесконечности. Понятие односторонних пределов. Необходимое и достаточное условие существования предела функции в конечной точке.
32. Бесконечно малые и бесконечно большие функции, взаимосвязь между ними. Основные свойства бесконечно малых и больших функций. Неопределённые выражения.
33. Основные свойства пределов функций (о пределах арифметических операций над функциями, имеющими конечный предел; о пределе элементарной функции; о предельном переходе в неравенствах).
34. Первый и второй замечательные пределы, их применение при вычислении пределов.
35. Определения непрерывности функции в точке. Точки разрыва функции, их классификация.
36. Понятие непрерывности на отрезке. Основные свойства функций, непрерывных на отрезке.
37. Приращение функции. Определение производной и её геометрический смысл. Непосредственное нахождение производной.
38. Касательная и нормаль к кривой в данной точке, их уравнения. Производные высших порядков.
39. Дифференциалы функции. Применение первого дифференциала в приближённых вычислениях.
40. Простейшие правила вычисления производной (постоянной, суммы, разности, произведения и частного функций).
41. Правило вычисления производной сложной функции.
42. Производные основных элементарных функций.
43. Правило Лопиталя и его применение для раскрытия неопределённостей: 
44. Достаточный признак монотонности функции. Стационарные и критические точки функции. Нахождение интервалов монотонности функции.
45. Точки локального экстремума (максимума и минимума) и локальные экстремумы функции. Необходимое и достаточные условия существования локального экстремума функции.
46. Наибольшее и наименьшее значения функции на отрезке, их нахождение.
47. Понятия выпуклости и вогнутости функции. Достаточный признак выпуклости (вогнутости) функции на интервале. Нахождение интервалов выпуклости и вогнутости функции. Точка перегиба графика функции, условия её существования и нахождение.
48. Понятие асимптоты графика функции. Вертикальные и наклонные асимптоты, условия их существования и нахождение.
49. Понятие функции 2-х переменных. Естественная область определения ФНП, график функции 2-х переменных, линии уровня.
50. Частные и полное приращения ФНП. Частные производные первого и высших порядков, их нахождение. Независимость смешанных производных от порядка дифференцирования.
51. Дифференциалы ФНП первого и второго порядков, их нахождение. Применение первого дифференциала в приближённых вычислениях.
52. Стационарные и критические точки. Точки локального экстремума (максимума и минимума) и локальные экстремумы ФНП. Необходимое и достаточное условия локального экстремума ФНП.
53. Глобальные экстремумы (наибольшее и наименьшее значения) ФНП в ограниченной и замкнутой области, их нахождение.
Раздел III. Интегральное исчисление.
54. Первообразная функция, её основные свойства.
55. Неопределённый интеграл, условия его существования и основные свойства.
56. Основные методы интегрирования: непосредственное интегрирование, интегрирование заменой переменной и по частям.
57. Вычисление интегралов вида:
А) , б) , в) , г) .
58. Определенный интеграл как предел интегральной суммы, его геометрический смысл. Условия существования определённого интеграла. Основные свойства определенного интеграла.
59. Интеграл с переменным верхним пределом и его свойства. Формула Ньютона-Лейбница.
60. Формулы замены переменной и интегрирования по частям в определённом интеграле.
61. Определённый интеграл и его применение для вычисления площади плоской фигуры, длины дуги плоской кривой, объёма тела вращения.
62. Несобственные интегралы по бесконечному промежутку интегрирования.
Раздел IV. Дифференциальные уравнения.
63. Понятие дифференциального уравнения первого порядка, различные формы его записи. Решение, начальные условия, общее и частное решения ДУ первого порядка. Задача Коши.
64. ДУ с разделёнными и разделяющимися переменными, их решение.
65. Однородное ДУ первого порядка, его решение.
66. Линейное ДУ первого порядка, его решение. Уравнение Бернулли.
67. ДУ порядка 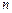 , различные формы его записи. Решение, начальные условия, общее и частное решения. Задача Коши.
, различные формы его записи. Решение, начальные условия, общее и частное решения. Задача Коши.
68. ДУ второго порядка, допускающие понижение порядка.
