Напряжение при чистом изгибе

Рассмотрим наиболее простой случай изгиба, называемый чис­тым изгибом и выведем формулу для определения нормальных напряжений для данного случая. Отметим, что методами теории упругости можно получить точную зависимость для нормальных напряжений при чистом изгибе, если же решать эту задачу методами сопротивления материалов, необходимо ввести некоторые допущения.

Таких гипотез при изгибе три:

1) гипотеза плоских сечений (гипотеза Бернулли). Сечения плоские до деформации остаются плоскими и после деформации, а лишь поворачиваются относительно некоторой линии, которая называется нейтральной осью сечения балки. При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой - сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;

2) гипотеза о постоянстве нормальных напряжений - напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

3) гипотеза об отсутствии боковых давлений - соседние продольные волокна не давят друг на друга.

Как было отмечено выше, под чистым изгибом понимается такой вид сопротивления, при котором в поперечных сечениях бруса возникают только изгибающие моменты, а попе­речные силы равны нулю. Для тех участков бруса, где соблюдается данное условие, изгибающий момент, вдоль продольной оси z принимает постоянное значение. Так как в любом сечении стержня при чистом изгибе 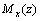= const, то для однородного бруса постоянного поперечного сечения изменение кривизны постоянно вдоль оси z. Под действием изгибающих мо­ментов ось бруса искривляется. Исходя из этого, ось бруса прини­мает форму дуги окружности с радиусом кривизны 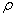(рис. 6.26). В данном случае с высокой степенью точности справедлива гипотеза плоских сечений. Следовательно, точки, расположенные до изгиба в плоскости поперечного сечения бруса, в результате изгиба пере­местятся в пространстве таким образом, что их совокупность снова образует плоскость.

Процесс формирования деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сече­ний друг относительно друга.

Рассмотрим два смежных сечения, отстоящих один от другого на расстоянии 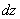(рис. 6.26).

В результате изгиба эти сечения наклонятся, образуя между со­бой угол 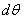, в связи с чем верхние волокна удлиняются, а ниж­ние - укоротятся. Очевидно, что при этом существует слой, длина которого не изменилась. Назовем его нейтральным слоем и обозначим отрезком СD. При этом 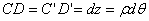. Произвольный отрезок АВ, расположен­ный от СD на расстоянии y, в результате изгиба удлинится на величину 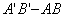. С учетом построений, изображенных на рис. 6.26, легко определить величину его линейной деформации:

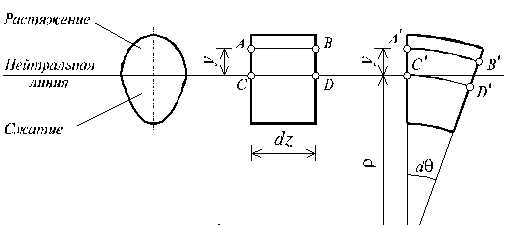
Рис.6.26

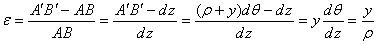. (1)

Если предположить, что продольные волокна не давят друг на друга, то каждое из них будет находиться в условиях простого растяжения - сжатия. Тогда переход от деформаций к нормальным напряжениям 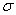можно осуществить посредством закона Гука: 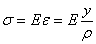(2)

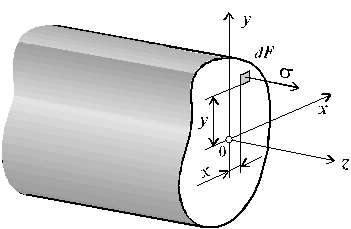
Рис. 6.27

Устано­вим положение нейт­ральной оси x, от кото­рой происходит отсчет координаты у (рис.6.27). Учитывая, что сумма элементарных сил 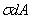по площади попе­речного сечения A дает нормальную силу 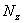. Но при чистом изгибе 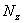= 0, следовательно:

.

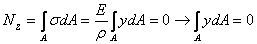Как известно, последний интеграл представляет собой статиче­ский момент сечения относительно нейтральной линии (оси x). Статический момент равен нулю, значит, нейтральная линия про­ходит через центр тяжести сечения.

Выразим момент внутренних сил относительно нейтральной оси 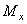через 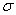. Очевидно, что

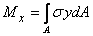. (3)

C учетом выражения (2) получим:

.

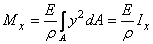Откуда

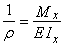, (4)

где 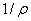- кривизна нейтрального волокна; EI_x - жесткость бруса.

Из формулы (3), исключая 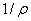, окончательно получим:

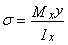. (5)

Эта формула была впервые получена Ш. Кулоном в 1773 году.

Откуда следует, что нормальные напряжения 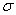в поперечном сече­нии бруса при его изгибе изменяются по линейному закону в зависимости от координаты y и принимают максимальное значение на уровне крайних волокон (при ):

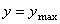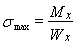, (6)

где 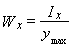- момент сопротивления сечения при изгибе.

Для прямоугольника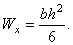

Для круга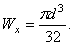

Для прокатных профилей (двутавра, швеллера, уголка) 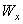приводится в таблицах сортамента.

Формулой (6) удобно пользоваться для расчета балок пластичного материала в упругой области, одинаково работающего на растяжение и сжатие. Поскольку знак напряжения в этом случае не имеет значения, напряжения вычисляются по модулю, и условие прочности при изгибе балки в форме призматического стержня получает вид

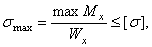(7)

где 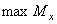— максимальное значение изгибающего момента (легко определяемое по его эпюре), 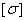- допускаемое напряжение на простое растяжение (сжатие). Напомним, что чистый изгиб балки сводится к растяжению и сжатию ее волокон (неравномерному в отличие от деформации растяжения (сжатия) призматического стержня, при котором ).

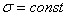При расчете балок из хрупких материалов следует различать наибольшие растягивающие 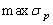и наибольшие сжимающие 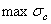напряжения, которые также определяются по модулю непосредственно и сравниваются с допускаемыми напряжениями на растяжение 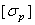и сжатие 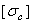. Условие прочности в этом случае будет иметь вид:

.

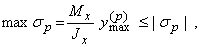
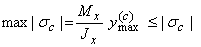Из условия (7) формулируют три рода задач на прочность при изгибе:

1) Проверка прочности: задана балка, нагрузка, известен материал. Строится эпюра 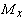- определяется 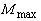, вычисляется 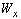и по (7) проверяется условие прочности.

2. Определение максимально допустимой нагрузки по условию прочности.

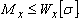(8)

Заданы размеры балки, характер нагрузки, материал балки.

Строится эпюра 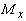- определяется 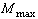от параметра нагрузки, вычисляется 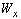и по (8) находят наибольший параметр нагрузки.

3. Конструирование балки – определение размеров ее поперечного сечения.

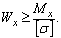(9)

Строится эпюра 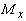- определяется 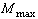, вычисляется правая часть (9) и подбираются размеры поперечного сечения, удовлетворяющие (9).

Для прямоугольного сечения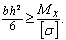

Обычно задаются отношением 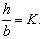(10)

Тогда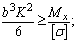

отсюда 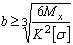. (11)

Задаваясь шириной 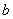по (10) получим .

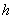Для двутаврового сечения по таблице сортамента подбирают номер двутавра с 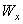большим, чем правая часть (9).

Энергия упругих деформаций бруса при изгибе V определяется работой момента 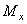на соответствующем угловом перемещении :

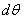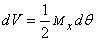, с учетом 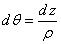и ,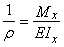

окончательно получим

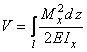. (12)