Частотные передаточные функции и частотные характеристики типовых звеньев
| Название | 1. Статическое безинерционное звено |
| Описание во временной области: | |
| ДУ | y = kx |
| ПФ | W(s) = k |
| Коэффициенты (параметры) | k – коэффициент передачи |
| Переходные характеристики | 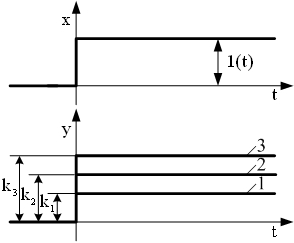 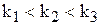 |
| Описание в частотной области: | |
| Частотная ПФ | Общая форма: W(jw) = k Алгебраическая форма: W(jw) = k + j0 |
| Частотные характеристики | 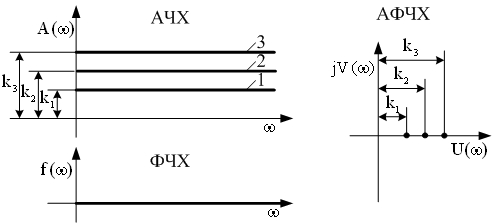 |
| Название | 2. Статическое апериодическое инерционное звено 1-го порядка. |
| Описание во временной области: | |
| ДУ | (Tp + 1)y = kx |
| ПФ | W(s) = 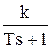 |
| Коэф-фициенты (параметры) | k – коэффициент передачи Т – постоянная времени, характеризующая инерционность |
| Переходные характерис-тики | 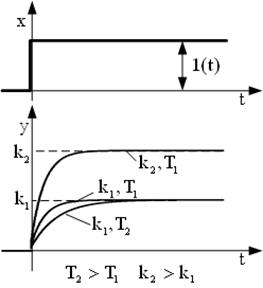 |
| Описание в частотной области: | |
| Частотная ПФ | Общая форма: W(jw) = 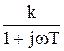 Алгебраическая форма: W(jw) = Алгебраическая форма: W(jw) = 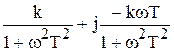 |
| Частотные харак-теристики | 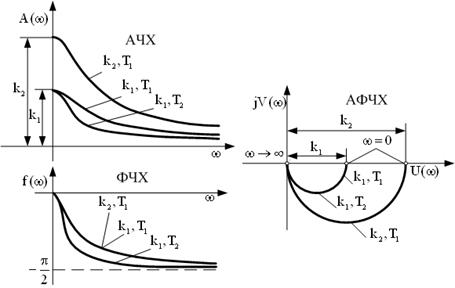 |
| Название | 3. Статическое апериодическое инерционное звено 2-го порядка |
| Описание во временной области: | |
| ДУ | (T1T2p2 + (T1 + T2)p +1)y = kx |
| ПФ | W(s) = 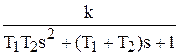 |
| Коэф-фициенты (параметры) | k – коэффициент передачи Т – постоянная времени, характеризующая инерционность |
| Переходные характерис -тики | 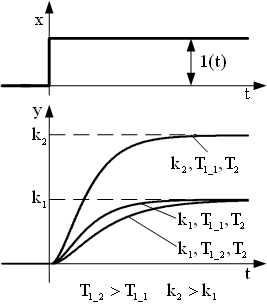 |
| Описание в частотной области: | |
| Частотная ПФ | Общая форма: W(jw) = 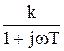 Алгебраическая форма: W(jw) = Алгебраическая форма: W(jw) = 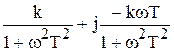 |
| Частотные харак-теристики | 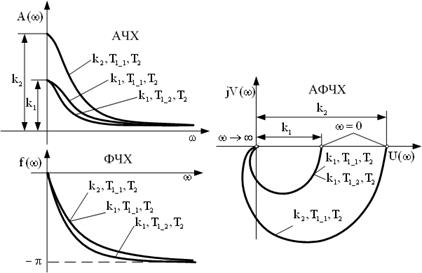 |
| Название | 4. Статическое колебательное инерционное звено 2 порядка |
| Описание во временной области: | |
| ДУ | (T2p2 + 2xTp + 1)y = kx, 0 < x < 1 |
| ПФ | W(s) = 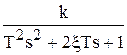 |
| Коэф-фициенты (параметры) | k – коэффициент передачи Т – постоянная времени, характеризующая инерционность x - коэффициент колебательности |
| Переходные характерис -тики | 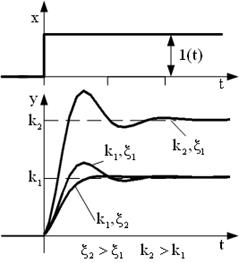 |
| Описание в частотной области: | |
| Частотная ПФ | W(jw) = 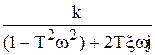 W(jw) = W(jw) = 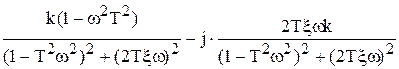 . . |
| Частотные харак-теристики | 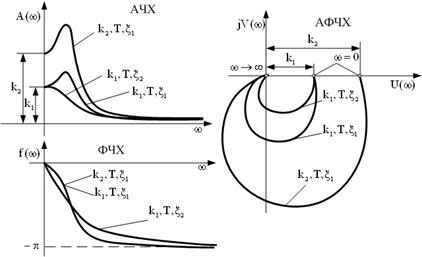 |
| Название | 5. Астатическое (интегрирующее) звено I порядка идеальное | |
| Описание во временной области: | ||
| ДУ | Tpy = x | |
| ПФ | W(s) = 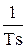 | |
| Коэф-фициенты (параметры) | Т – постоянная времени интегрирования | |
| Переходные характерис -тики | 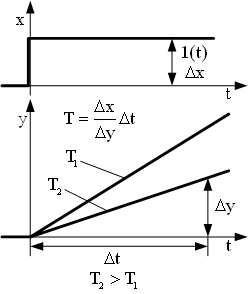 | |
| Описание в частотной области: | ||
| Частотная ПФ | W(jw) = 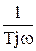 W(jw) = W(jw) = 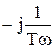 | |
| Частотные харак-теристики | 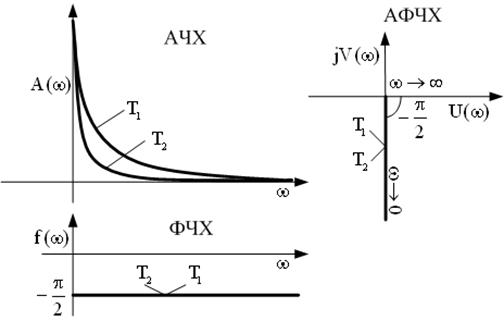 | |
| Название | 6. Астатическое (интегрирующее) звено с замедлением | |
| Описание во временной области: | ||
| ДУ | (T1T2p2 + T1p)y = x | |
| ПФ | W(s) =  | |
| Коэф-фициенты (параметры) | 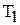 – постоянная времени интегрирования – постоянная времени интегрирования 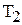 - постоянная времени - постоянная времени | |
| Переходные характерис -тики | 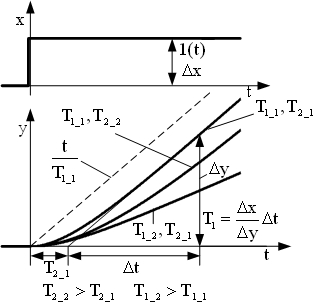 | |
| Описание в частотной области: | ||
| Частотная ПФ | W(jw) = 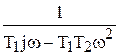 W(jw) = W(jw) = 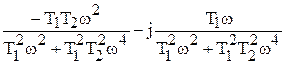 | |
| Частотные харак-теристики | 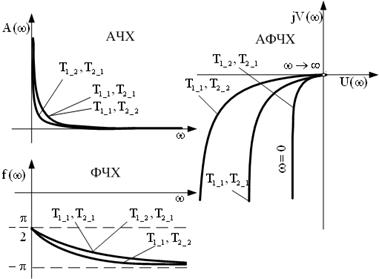 | |
| Название | 7. Астатическое изодромное звено | |
| Описание во временной области: | ||
| ДУ | Tpy = (Tp + 1)x | |
| ПФ | W(s) = 1 + 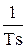 | |
| Коэф-фициенты (параметры) | Т – постоянная времени | |
| Переходные характерис -тики | 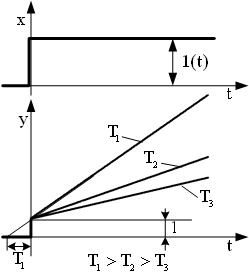 | |
| Описание в частотной области: | ||
| Частотная ПФ | W(jw) = 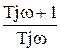 W(jw) = 1 - j W(jw) = 1 - j 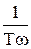 | |
| Частотные харак-теристики | 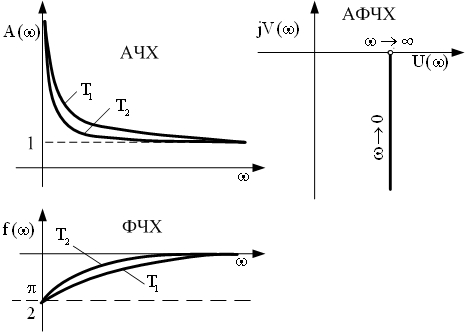 | |
| Название | 8. Дифференцирующее идеальное звено I порядка | |
| Описание во временной области: | ||
| ДУ | y = Tpx | |
| ПФ | W(s) = Ts | |
| Коэф-фициенты (параметры) | Т – постоянная времени | |
| Переходные характерис -тики | 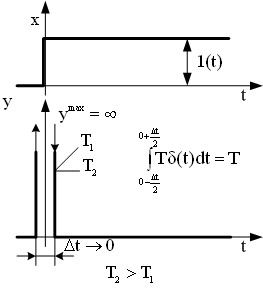 | |
| Описание в частотной области: | ||
| Частотная ПФ | W(jw) = Tjw W(jw) = Tjw | |
| Частотные харак-теристики | 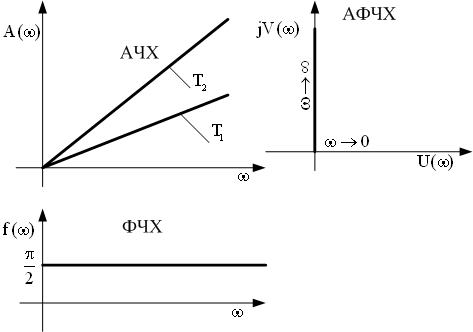 | |
| Название | 9. Дифференцирующее реальное звено (с замедлением) 1-го порядка |
| Описание во временной области: | |
| ДУ | (T1p + 1)y = T2px |
| ПФ | W(s) = 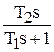 |
| Коэф-фициенты (параметры) | Т1, Т2 – постоянные времени |
| Переходные характерис -тики | 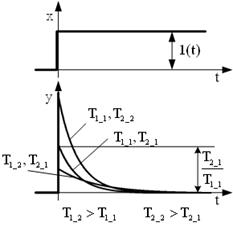 |
| Описание в частотной области: | |
| Частотная ПФ | W(jw) = 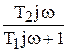 W(jw) = W(jw) = 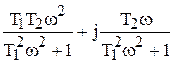 |
| Частотные харак-теристики | 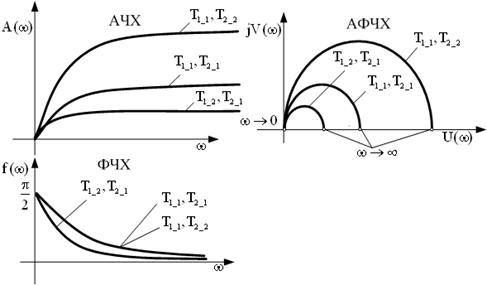 |
| Название | 10. Звено чистого запаздывания |
| Описание во временной области: | |
| ДУ | y = x(t -t) |
| ПФ | W(s) = 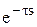 |
| Коэф-фициенты (параметры) | 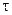 - время запаздывания - время запаздывания |
| Переходные характерис -тики | 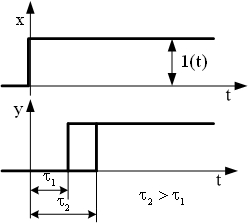 |
| Описание в частотной области: | |
| Частотная ПФ | W(jw) = 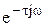 W(jw) = coswt - jsinwt W(jw) = coswt - jsinwt |
| Частотные харак-теристики | 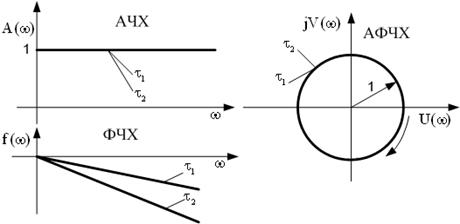 |
