Сложение двух параллельных сил.
Лекция №3. Момент силы относительно точки. Момент силы относительно оси. Сложение двух параллельных сил. Теория пар.
Момент силы относительно точки.
 Рассмотрим силу
Рассмотрим силу 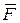 , приложенную к телу в точке А. Из некоторого центра О опустим перпендикуляр на линию действия силы
, приложенную к телу в точке А. Из некоторого центра О опустим перпендикуляр на линию действия силы 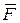 .
.
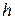 - плечо действия силы.
- плечо действия силы.
Моментом силы относительно какой – либо точки (центра) называется вектор численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, проходящей через выбранную точку и линию действия силы в ту сторону, откуда вращение видно происходящим против часовой стрелки.
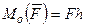
Момент силы характеризует ее вращательное действие. Справедливо соотношение:
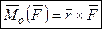
т.к. 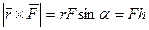 .
.
Т.к. векторное произведение векторов равно площади параллелограмма, построенного на этих векторах, то
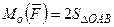
Пусть точка 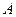 имеет координаты
имеет координаты 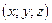 ,
, 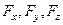 - проекции силы на координатные оси. Тогда
- проекции силы на координатные оси. Тогда
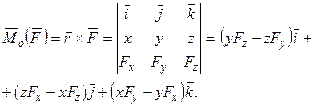 (3.1)
(3.1)
Таким образом, проекции момента силы на координатные оси определяются формулами:
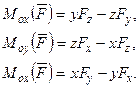

 Рассмотрим силу, расположенную в плоскости
Рассмотрим силу, расположенную в плоскости 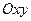 как показано на рис. . Определим момент силы относительно центра
как показано на рис. . Определим момент силы относительно центра 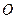 .
.
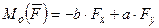
Момент силы относительно оси.
Пусть на тело действует некоторая сила 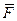 . Найдем проекцию этой силы на плоскость
. Найдем проекцию этой силы на плоскость 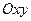 и момент этой проекции относительно точки
и момент этой проекции относительно точки 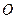 . Тогда, с учетом того, что для проекции
. Тогда, с учетом того, что для проекции 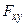 выполняется
выполняется 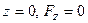 , на основании равенства (3.1) можно записать
, на основании равенства (3.1) можно записать
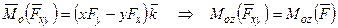 .
.
Таким образом, момент проекции силы равен проекции момента силы.
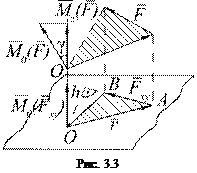 Проекция вектора
Проекция вектора 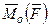 , т.е. момента силы относительно центра
, т.е. момента силы относительно центра 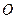 на какую-нибудь ось
на какую-нибудь ось 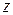 , проходящую через этот центр, называется моментом силы относительно оси.
, проходящую через этот центр, называется моментом силы относительно оси.
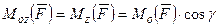 ,
,
где 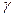 - угол между
- угол между 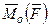 и
и 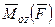
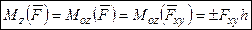
«+»: когда с положительного конца оси 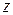 поворот, который стремится совершить сила
поворот, который стремится совершить сила 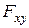 , виден происходящим против хода часовой стрелки.
, виден происходящим против хода часовой стрелки.
«-»: по ходу часовой стрелки.
Правило вычисления момента относительно оси :
1. выбрать на оси произвольную точку и построить плоскость, перпендикулярную оси;
2. спроектировать на эту плоскость силы;
3. определить плечо проекции силы 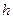 ;
;
4. вычислить произведение 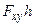 ;
;
5. определить знак момента.
Момент силы относительно оси равен нулю, если:
1. сил параллельна оси (т.к. 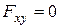 );
);
2. линия действия силы пересекает ось ( 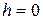 ).
).
 Пример. Вычислить момент относительно точки
Пример. Вычислить момент относительно точки 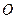 и координатных осей силы
и координатных осей силы 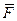 , приложенной к точке
, приложенной к точке 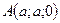 и направленной по диагонали куба со стороной
и направленной по диагонали куба со стороной 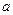 .
.
Найдем проекции силы на координатные плоскости:
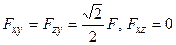 .
.
Тогда 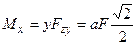 ,
, 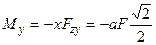 ,
, 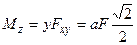 .
.
Модуль момента относительно точки 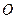 определится равенством:
определится равенством:
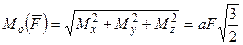 .
.
Сложение двух параллельных сил.
1. Пусть на тело действуют две параллельные силы 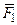 и
и 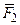 , приложенные соответственно в точках
, приложенные соответственно в точках 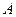 и
и 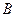 . Требуется найти их сумму. Рассмотрим случай, когда силы направлены в одну сторону (
. Требуется найти их сумму. Рассмотрим случай, когда силы направлены в одну сторону ( 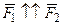 ).Выполним дополнительные построения:
).Выполним дополнительные построения:
1. Добавим уравновешенную систему сил 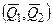 , приложенных в точках
, приложенных в точках 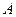 и
и 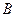 ;
;
2. Т.к. 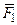 и
и 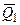 - сходящиеся, то у них существует равнодействующая, приложенная к той же точке
- сходящиеся, то у них существует равнодействующая, приложенная к той же точке 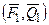 ~
~ 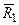 , аналогично
, аналогично 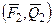 ~
~ 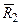 ; пусть линии действия сил
; пусть линии действия сил 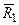 и
и 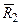 пересекаются в некоторой точке
пересекаются в некоторой точке 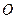 ;
;
3. Перенесем силы 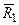 и
и 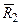 в точку
в точку 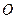 и разложим на составляющие
и разложим на составляющие 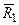 ~
~ 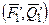 ,
, 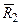 ~
~ 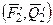 ;
;
4. 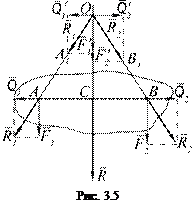 Т.к.
Т.к. 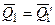 ,
, 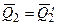 , то система сил
, то система сил 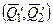 также является уравновешенной, следовательно ее можно отбросить,
также является уравновешенной, следовательно ее можно отбросить,
5. 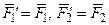 , силы
, силы 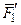 и
и 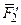 , действуют вдоль одной прямой, следовательно, их можно заменить одной силой – равнодействующей
, действуют вдоль одной прямой, следовательно, их можно заменить одной силой – равнодействующей 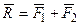 , причем
, причем
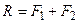 (3.2)
(3.2)
Рассмотрим треугольники 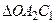 ~
~ 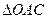 ,
, 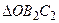 ~
~ 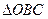 , тогда
, тогда
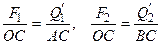
Разделим эти равенства, с учетом того, что 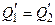 , получим:
, получим:
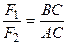 (3.3)
(3.3)
Вывод: Система двух параллельных сил, направленных в одну сторону, имеет равнодействующую, параллельную этим силам и направленную в ту же сторону, причем ее модуль равен сумме модулей слагаемых сил; точка приложения равнодействующей делит расстояние между точками приложения слагаемых сил внутренним образом на части, обратно пропорциональные модулям этих сил.
2. Рассмотрим случай, когда силы направлены в разные стороны и не равны по модулю. Пусть 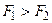 :
:
1.  Разложим силу
Разложим силу 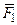 на составляющие
на составляющие 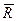 и
и 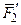 , так что
, так что 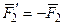 и приложена в точке
и приложена в точке 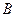 , т.е.
, т.е. 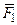 ~
~ 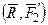
2. Тогда 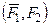 ~
~ 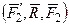 , но
, но 
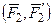 ~
~ 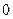 , поэтому
, поэтому 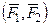 ~
~ 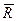 , т.е.
, т.е. 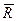 - равнодействующая.
- равнодействующая.
Определим модуль и место приложения равнодействующей.
Т.к. 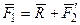 , то
, то 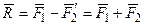 , а следовательно, модуль равнодействующей
, а следовательно, модуль равнодействующей
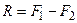 (3.4)
(3.4)
Согласно (3.3) 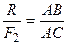 . Тогда с учетом (3.4), получим:
. Тогда с учетом (3.4), получим: 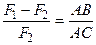 ,
,
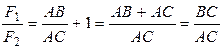 .
.
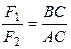 . (3.5)
. (3.5)
Вывод: Две не равные по модулю противоположно направленные параллельные силы имеют равнодействующую, параллельную этим силам, направленную в сторону большей по модулю силы, причем ее модуль равен разности модулей слагаемых сил; линия действия равнодействующей делит расстояние между точками приложения слагаемых сил внешним образом на части, обратно пропорциональные модулям этих сил.
Пара сил. Момент пары.
Парой сил называется система двух сил, действующих на абсолютно твердое тело, равных по модулю и противоположных по направлению.
ОБРАТИТЕ ВНИМАНИЕ! Пара сил, не представляет собой уравновешенную систему сил.

Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.
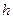 - плечо пары.
- плечо пары.
Моментом пары сил называется вектор 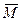 , модуль которого равен произведению модуля одной из сил пары на плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
, модуль которого равен произведению модуля одной из сил пары на плечо и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки.
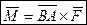 ,
, 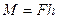
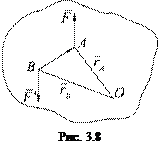
Теорема(о моменте пары)
Момент пары равен сумме моментов относительно любого центра  сил, образующих пару, т.е.
сил, образующих пару, т.е.
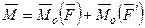 .
.
▲ 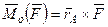 ,
, 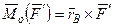 ,
,
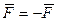 ,
, 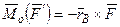 , тогда,
, тогда,
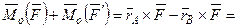
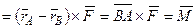 ∆
∆
