Теория метода и описание установки. Определение коэффициентов силы сухого трения
Лабораторная №8
Определение коэффициентов силы сухого трения
Цель работы: определить коэффициенты трения покоя, скольжения и качения при качении шарика по наклонной плоскости.
Приборы и оборудование:установка, шарик, миллиметровая бумага.
Теория метода и описание установки
Если тело (шарик) покоится на наклонной плоскости, то на него действует сила трения покоя. Она всегда равна по величине и противоположна по направлению внешней силе, стремящейся вызвать движение тела. Однако существует максимальное значение силы трения покоя, определяемое формулой
F=kN ,
где k-коэффициент трения покоя; N- сила нормального давления (сила реакции опоры). Значение k зависит от свойств поверхностей соприкасающихся тел.
Если тело движется со скольжением, то возникает сила трения скольжения 
Она направлена вдоль поверхности соприкосновения двух тел и противоположна скорости движения тела. Коэффициент трения скольжения 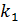 зависит также от относительной скорости трущихся поверхностей. Если скорость движения тела не слишком велика, то значение
зависит также от относительной скорости трущихся поверхностей. Если скорость движения тела не слишком велика, то значение 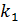 можно считать постоянным и равным значению k, т.е.
можно считать постоянным и равным значению k, т.е. 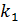 ≈k.
≈k.
При качении тела по плоскости возникает деформация плоскости и катящего тела. Вследствие этого сила реакции опоры не проходит через центр тяжести тела, а смещена вперед по движению. Это приводит к появлению момента силы реакции опоры относительно оси вращения катящегося тела. Данный момент силы препятствует качению (вращению) тела и называется момент силы трения качения. Его значение вычисляется по формуле
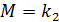 *N,
*N,
где 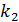 - коэффициент момента силы трения качения. Существенное отличие его от коэффициентов k и
- коэффициент момента силы трения качения. Существенное отличие его от коэффициентов k и 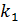 состоит в том, что эта величина имеет размерность длины и характеризует плечо силы реакции опоры относительно оси вращения тела.
состоит в том, что эта величина имеет размерность длины и характеризует плечо силы реакции опоры относительно оси вращения тела.
Коэффициенты k, 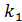 ,
, 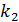 можно определить из измерений ускорения при движении шарика по желобу.
можно определить из измерений ускорения при движении шарика по желобу.
1. При незначительных углах наклона желоба к горизонту шарик, находящийся в желобе, будет находиться в состоянии покоя.Наибольший угол, при котором шарик ещё не начинает скатываться, получим из условий равновесия:
mg 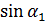 -F=0,
-F=0,
Fr- 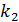 mg
mg 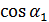 =0;
=0;
где m-масса шарика; F-параллельная плоскости сила трения покоя;
g-ускорение силы тяжести; r- плечо силы F.
Эти уравнения дают 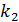 =r
=r 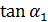 .
.
2. При увеличении угла наклона желоба с угла α= 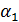 начинается качение шарика без скольжения. Для желоба прямоугольного сечения уравнения движения шарика запишутся в виде
начинается качение шарика без скольжения. Для желоба прямоугольного сечения уравнения движения шарика запишутся в виде
ma= mg 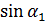 –F,
–F,
mg 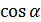 -N=0,
-N=0,
Jε=Fr- 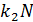 ,
,
a=rε,
где J=  m
m 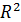 -момент инерции шарика; r=R
-момент инерции шарика; r=R 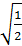 (R-радиус шарика); а-ускорение движения центра масс шарика, ε-угловое ускорение.
(R-радиус шарика); а-ускорение движения центра масс шарика, ε-угловое ускорение.
Из этих уравнений получим:
F=  mg(4
mg(4 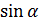 +5
+5 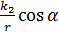 )
)
определяет наибольшее значение угла 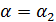 , при котором ещё возможно движение без скольжения. Получим:
, при котором ещё возможно движение без скольжения. Получим:
k= 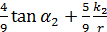
Для этого угла, полагая 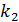 =0,
=0,
k= 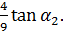
3.При дальнейшем увеличении угла наклона желоба с некоторого угла 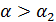 движении шарика можно считать чистым скольжением.
движении шарика можно считать чистым скольжением.
Уравнения движения будут иметь вид
ma= mg 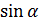 -
- 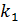 mg
mg 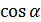 ,
,
где а-ускорение центра масс шарика. Его значение вычисляется по формуле
а= 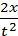 ,
,
где х-длина желоба, t-время движения шарика по желобу.
Получим:
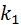 =
= 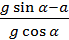 .
.
Для определения углов 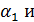
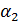 вычисляют ускорение центра масс шарика без учёта силы трения по формуле:
вычисляют ускорение центра масс шарика без учёта силы трения по формуле:
j=  g
g 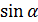 .
.
Значение 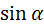 вычисляют по уравнению
вычисляют по уравнению
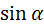 =
=  , где h-высота поднятия желоба.
, где h-высота поднятия желоба.
Основная часть установки- металлический желоб прямоугольного сечения длиной 138 см. Он может поворачиваться вокруг горизонтальной оси, проходящей через его нижний конец.
При помощи винта желоб может фиксироваться в нужном положении. На вертикальной стойке закреплена шкала для определения высоты, с которой скатывается шарик. Внутренняя поверхность желоба покрыта лентой из легкодеформирующегося материала. Электромагнит на верхнем конце желоба удерживает шарик. На нижнем конце желоба имеется стержень, смещаемый ударом движущегося шарика.
Электромагнит и стержень связаны с электрическим секундомером, измеряющим время движения шарика по желобу. При нажатии на кнопку электромагнит освобождает шарик и включает секундомер. При ударе шарика о стержень секундомер останавливается.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Установить металлический желоб на минимальной высоте.
2. Измерить 3 раза время движения шарика, вычислить среднее арифметическое значение t из 3 замеров времени и занести в таблицу.
3. Определить ускорение движения центра масс шарика а.
4. Вычислить значение 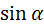 . Используя таблицы В.М.Брадиса, найти угол
. Используя таблицы В.М.Брадиса, найти угол 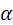 для данной высоты желоба.
для данной высоты желоба.
5. Определить ускорение движения центра масс шарика без учёта трения качения.
6. Последовательно поднимая металлический желоб на 5 см до максимальной высоты, выполнить п.2-5 для каждой высоты.
Дано: r=1,25 см, х=138 см, 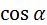 =
= 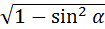 .
.
| № п/п | h,м | t,с | 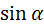 | α,град | а, 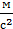 | j, 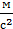 |
| 0,1 | 2,7 | 0,109 | 0,379 | 0,38 | ||
| 0,15 | 0,15 | 0,1725 | 0,60 | |||
| 0,2 | 4,32 | 0,18 | 0,15 | 0,79 |
Контрольные вопросы:
1. Какова причина возникновения силы трения качения?
2. В чем заключается физический смысл коэффициента силы трения качения?
3. Запишите уравнения движения для шарика, катящегося по наклонной плоскости.
1. При соприкосновении движущихся (или приходящих в движение) тел с другими телами, а также с частицами вещества окружающей среды возникают силы, препятствующие такому движению. Эти силы называют силами трения. Действие сил трения всегда сопровождается превращением механической энергии во внутреннюю и вызывает нагревание тел и окружающей их среды.
