Поверхности вращения – это поверхности созданные при вращении образующей mвокруг оси i

Геометрическая часть определителя состоит из двух линий: образующей m и оси i.

Алгоритмическая часть включает две операции:

1. На образующей m выделяют ряд точек A, B, C, …F;

2. Каждую точку вращают вокруг оси i.

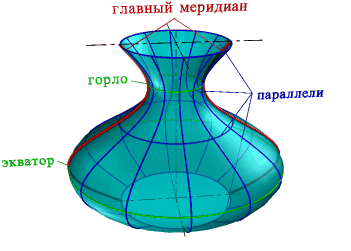
Так создается каркас поверхности, состоящей из множества окружностей, плоскости которых расположены перпендикулярно оси i. Эти окружности называются параллелями; наименьшая параллель называется горлом, наибольшая – экватором.

Из закона образования поверхности вращения вытекают два основных свойства:

1. Плоскость перпендикулярная оси вращения, пересекает поверхность по окружности – параллели.

2. Плоскость, проходящая через ось вращения, пересекает поверхность по двум

симметричным относительно оси линиям – меридианам.

Плоскость проходящая через ось параллельно фронтальной плоскости проекций называется плоскостью главного меридиана, а линия, полученная в сечении, – главным меридианом.

Рассмотрим наиболее распространенные поверхности вращения с криволинейными образующими:

Сфера – образуется вращением окружности вокруг её диаметра (рис.8.6).

При сжатии или растяжении сферы она преобразуется в эллипсоиды, которые могут быть получены вращением эллипса вокруг одной из осей: если вращение вокруг большой оси то эллипсоид называется вытянутым (рис.8.8), если вокруг малой – сжатым или сфероидом (рис.8.7).

Тор– поверхность тора формируется при вращении окружности вокруг оси, не проходящей через центр окружности (рис.8.9).

Параболоид вращения– образуется при вращении параболы вокруг своей оси.

Билеты 20 - 21:

Винтовые поверхности.

Винтовые поверхности образуются винтовым движением некоторой линии – образующей.

Под винтовым движением понимается совокупность двух движений: поступательного параллельно некоторой оси, и вращательного, вокруг той же оси.

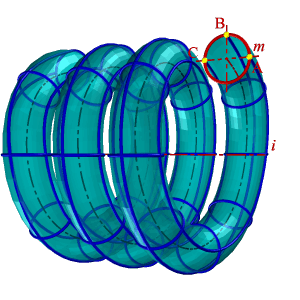	При этом поступательное и угловое перемещение находятся в определенной зависимости ∆h=k∆v, где ∆h – линейное перемещение за время ∆t, ∆v– угловое перемещение за то же время, k – коэффициент пропорциональности. Если k=Const, то шаг поверхности постоянный. Геометрическая часть определителя винтовой поверхности ни чем не отличается от поверхности вращения и состоит из двух линий: образующей m, и оси i(рис.8.12). Алгоритмическая часть: 1. На образующей m выделяют ряд точек А, В, С, … 2. Строят винтовые линии заданного шага и направления, по которым перемещаются заданные точки.
	Линейчатые поверхности с плоскостью параллелизма (поверхности каталана).

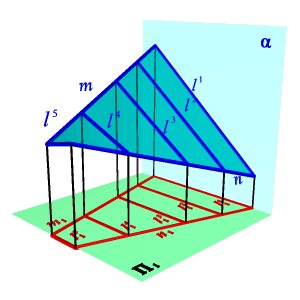
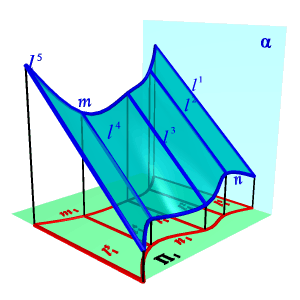Поверхность с плоскостью параллелизма представляет собой множество прямых линий l (образующих), параллельных некоторой плоскости α (плоскости параллелизма) и пересекающих две данные направляющие m, n (рис. 8.13). В зависимости от формы направляющих образуются три частных вида поверхностей. Цилиндроид. Цилиндроидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим кривым линиям, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.13). Коноид.Коноидом называется поверхность, образованная движением прямолинейной образующей по двум направляющим, одна из которых кривая линия, а другая прямая, при этом образующая во всех положениях параллельна плоскости параллелизма (рис.8.14).

Рисунок 8.13. Цилиндроид

Гиперболический параболоид. Гиперболическим параболоидом или косой плоскостью называется поверхность, образованная движением прямолинейной образующей, параллельной плоскости параллелизма, по двум направляющим линиям – скрещивающимся прямым (рис.8.15).

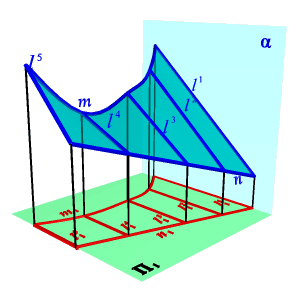Рисунок 8.14. Коноид	Рисунок. 8.15. Гиперболический параболоид

Билет 17:

Пересечение линии с поверхностью

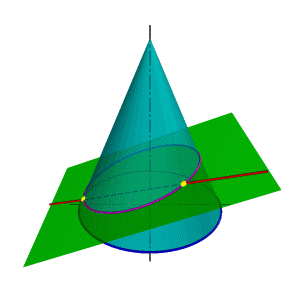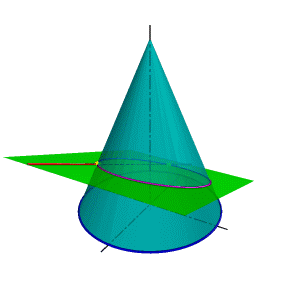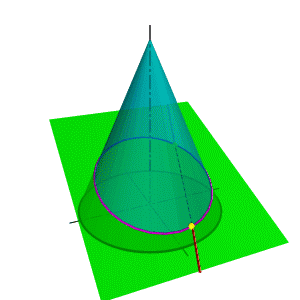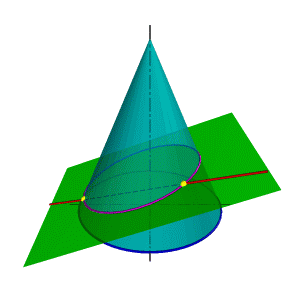
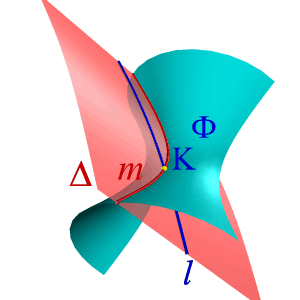	В общем случае для графического определения точек пересечения линии с поверхностью (рис.8.28) необходимо выполнить ряд геометрических построений, описываемых следующим алгоритмом: 1. Заключаем линию l в некоторую вспомогательную поверхность Δ; 1. Строим линию m пересечения данной поверхности Ф и вспомогательной поверхности Δ; 2. Определяем искомую точку К пересечения линии l и m (точка может быть не единственная). В качестве вспомогательной поверхности целесообразно использовать проецирующую цилиндрическую поверхность, направляющей которой должна служить заданная линия, а –прямолинейными образующими – проецирующие прямые. Пример: Определить точки пересечения прямой линии с поверхностью конуса вращения и определить видимость прямой по отношению к конусу. Если в качестве вспомогательной секущей плоскости можно выбрать горизонтально проецирующую или фронтально проецирующую плоскости, то в сечении получатся соответственно гипербола (рис.8.29а) или эллипс (рис.8.29б). Построение кривых линий значительно усложняет задачу.
	Рисунок 8.28. Пересечение линии с поверхностью

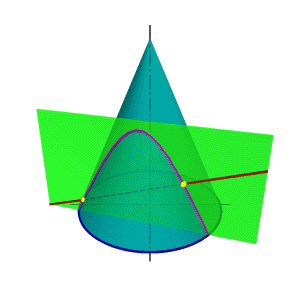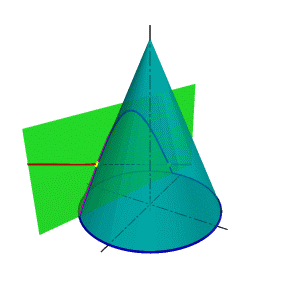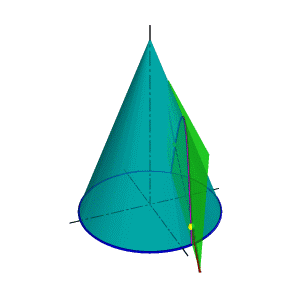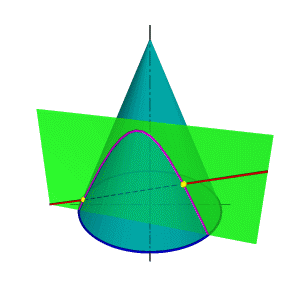а) горизонтально проецирующая плоскость	б) фронтально проецирующая плоскость
Рисунок 8.29 Пересечение прямой линии с конусом (вспомогательная секущая плоскость- проецирующая плоскость )

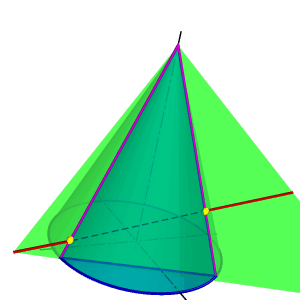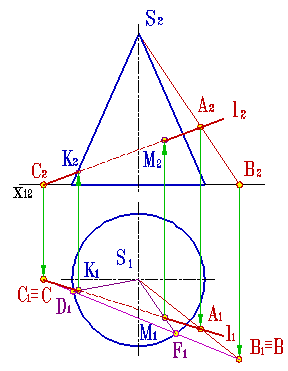			а) модель		б) эпюр
Рисунок 8.30. Пересечение прямой линии с конусом (вспомогательная секущая плоскость-плоскость общего положения)

Поэтому в качестве вспомогательной секущей плоскости целесообразно выбрать такую плоскость, которая бы включала прямую l и пересекала конус по образующим (рис.8.30). Очевидно, что такая плоскость определяется прямой l и точкой S- вершиной конуса. Пусть основание конуса лежит в горизонтальной плоскости проекций, тогда линия пересечения вспомогательной секущей плоскости и горизонтальной плоскости проекций ВС пересекает основание конуса в точках D и F. Таким образом в сечении конуса вспомогательной секущей плоскостью получится треугольник DFS. Так как полученный треугольник и прямая l лежат в одной плоскости, точки их пересечения К и Ми есть точки пересечения прямой с конусом.

Билет 27:

Развертка поверхности

Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).

Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.

Основные свойства развертки

1. Длины двух соответствующих линий поверхности и ее развертки равны между собой;

2. Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;

3. Прямой на поверхности соответствует также прямая на развертке;

4. Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;

5. Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.