Взаимосвязь свойств и функций состояния индивидуальных веществ при фазовых переходах. Уравнение Клапейрона-Клаузиуса, его дифференциальные и интегральные формы.
Фазовые переходы в таких системах сопровождаются изменением агрегатного состояния. Например, в процессе испарения жидкости устанавливается равновесие жидкость ⇄ пар; равновесие твёрдое тело ⇄ жидкость характеризует процесс плавления/кристаллизации. Особую группу составляют фазовые переходы в твердом теле:твёрдое тело(1)⇄ твёрдое тело(2). Они представляют собой структурные превращения (например, превращение графита в алмаз или структурные переходы в активных материалах, в частности, в сегнето- или антисегнетоэлектриках).
| Равновесия, названия процессов | Знак ΔНпроцесса (λпроцесса) | Знак ΔSпроцесса | Актуальность понимания | |
температурной зависимости равновесного давления паров 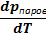 | барической зависимости температуры фазового перехода (фазового превращения) 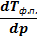 | |||
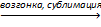 т ⇄ п т ⇄ п 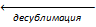 | λвозгонки≫0 | ΔSвозгонки ≫0 | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. | Данная зависимость редко анализируется. |
 ж ⇄ п ж ⇄ п  | λкипения >0 | ΔSкипения >0 | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. |
 т ⇄ ж т ⇄ ж  | λплавления ≳0 | ΔS плавления≳0 | Данная зависимость редко анализируется, т.к. в системе отсутствует собственная паровая фаза. | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. |
 т(1) ⇄ т(2) т(1) ⇄ т(2)  | λструкт.превр.≶0 | ΔSстр.пр. ≶0 | Данная зависимость редко анализируется, т.к. в системе отсутствует собственная паровая фаза. | Да, соответствующая зависимость имеет важное значение. Формулу для её анализа нужно получить. |
Вначале рассмотрим равновесие твёрдое тело ⇄ пар, которое называют процессом возгонки или сублимации. Затем кратко обоснуем вид аналогичных соотношений для других межфазных равновесий.
Пусть мы имеем в состоянии равновесия 1моль твердого вещества и 1моль его пара. Наличие динамического равновесия означает, что мольные изобарно-изотермические потенциалы соответствующих фаз совпадают: Gт = Gп. В предыдущей части лекции, посвященной обоснованию принципа Ле-Шателье, было показано, что увеличением температуры (на произвольную величину dT) и одновременным увеличением давления (на конкретную величину dp) можно добиться одинакового изменения энергии Гиббса обеих фаз (на dG), и перевести систему в новое равновесие. Для него будут равны новые значения изобарных потенциалов:
Gт + dGт = Gп + dGп.
Поскольку одновременно равны и первые слагаемые, следовательно, можем записать:
dGт = dGп.
Теперь используем связь полного дифференциала энергии Гиббса с ее характеристическими параметрами:
dG = VdP - SdT.
В итоге получаем:
Vтdp ‒ SтdT = Vпdp ‒ SпdT.
Перегруппируем слагаемые и поделим на dT: Sп - Sт = (Vп - Vт) 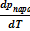 . (V.1)
. (V.1)
Слева имеем ΔSвозг. = Sп - Sт. По II-му началу термодинамики можем заменить эту разность на приведенную теплоту этого процесса:
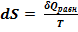 или в нашем случае для изобарно-изотермических условий ΔSвозг. =
или в нашем случае для изобарно-изотермических условий ΔSвозг. = 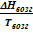 .
.
Выполняем замену в (V.1)и переносимТвозг в правую часть равенства:
ΔНвозг = Твозг(Vп - Vт) 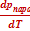 . (V.2)
. (V.2)
Уравнение (V.2) известно как уравнение Клапейрона-Клаузиуса для равновесия твердое тело ⇄ пар. Его можно упростить, принимая во внимание, что Vп ≫ Vт.
Получаем: ΔНвозг ≈ ТвозгVп 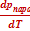 и
и 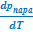 ≈
≈ 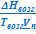 . (УрКл-Кл_1-диф)
. (УрКл-Кл_1-диф)
Важно отметить, что в правой части полученного равенства все величины положительны (в том числе и числитель, поскольку возгонка - безусловно эндотермический процесс, требующий затраты энергии на перевод твердого тела в газовую фазу). Таким образом, имеем:
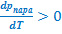 ,
,
что означает, что при увеличении температуры повышается равновесное давление пара над твердой фазой. Поэтому в р-Т координатах соответствующая межфазная граница должна иметь положительный угловой коэффициент. Кроме того, следует учесть, что такое равновесие следует ожидать при низких температурах (при высоких Т твердая фаза может не сохраниться и, скажем, расплавиться) и низких давлениях (при высоких р газовая фаза может сконденсироваться в жидкость). Таким образом, при охлаждении линия равновесия твёрдое тело ⇄ пар устремляется к началу координат (при Т → 0К рпаров также уменьшается до нуля). В то же время, в направлении высоких температур и давлений эта линия должна быть ограничена точкой, в которой появится вторая конденсированная фаза - жидкость:

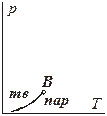 Кривизну линии обосновывать не станем. Строго говоря, она определяется второй производной функции р = f(T). При анализе этой зависимости удается показать, что функция р = f(T) обращена выпуклостью к оси температур. Молярную теплоту фазового перехода принято обозначать символом λ. Тогда можем записать:
Кривизну линии обосновывать не станем. Строго говоря, она определяется второй производной функции р = f(T). При анализе этой зависимости удается показать, что функция р = f(T) обращена выпуклостью к оси температур. Молярную теплоту фазового перехода принято обозначать символом λ. Тогда можем записать:
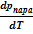 ≈
≈ 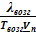 .
.
В свою очередь, барическая зависимость температуры возгонки описывается обратным соотношением:
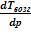 ≈
≈ 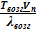 .
.
Если давление насыщенных паров невелико, то можно считать, что они (пары) обладают свойствами идеального газа ( 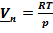 ):
):
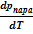 ≈
≈ 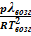 или
или 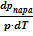 ≈
≈ 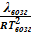 или
или 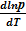 ≈
≈ 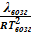 или
или 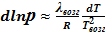 .
.
В небольшом интервале температур можно считать теплоту фазового перехода постоянной величиной. Тогда после интегрирования последнего уравнения получаем:
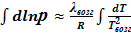 или
или 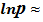 -
- 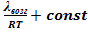 УрКл-Кл_1-инт
УрКл-Кл_1-инт
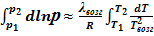 или
или 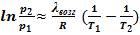 .УрКл-Кл_1-инт'
.УрКл-Кл_1-инт'
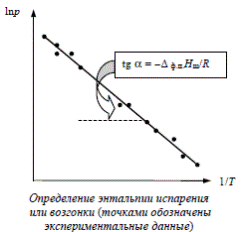 Полученные интегральные формы уравнения Клузиуса-Клапейрона позволяют рассчитывать энтальпии возгонки (термодинамическую характеристику соединения) по данным о давлении его насыщенных паров (физическая, механическая характеристика вещества). Например, первый вариант интегрального уравнения представляет собой уравнение прямой в координатах
Полученные интегральные формы уравнения Клузиуса-Клапейрона позволяют рассчитывать энтальпии возгонки (термодинамическую характеристику соединения) по данным о давлении его насыщенных паров (физическая, механическая характеристика вещества). Например, первый вариант интегрального уравнения представляет собой уравнение прямой в координатах 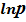 - 1/T:
- 1/T:
Соответственно, λвозг может быть найдена через угловой коэффициент прямой, построенной по экспериментальным значениям логарифма равновесного давления паров при разных температурах.
Расчет по второму уравнению менее надежен, поскольку в нем используются только два значения равновесного давления паров и, поэтому, больше вероятность ошибки, вносимой погрешностями эксперимента:
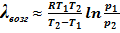 .
.
Из УрКл-Кл_1-инт' можно получить формулу температурной зависимости давления насыщенного пара:
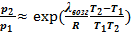 или
или 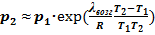 . Именно из этого выражения следует вид кривизны для линии равновесия твёрдое тело ⇄ пар на p-T-диаграмме. Уравнение это, как следует из её вывода, справедливо для небольшого интервала температур. Часто вместо приведенных формул используют эмпирические зависимости в виде степенных температурных рядов:
. Именно из этого выражения следует вид кривизны для линии равновесия твёрдое тело ⇄ пар на p-T-диаграмме. Уравнение это, как следует из её вывода, справедливо для небольшого интервала температур. Часто вместо приведенных формул используют эмпирические зависимости в виде степенных температурных рядов:
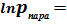 -
- 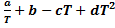 (константы разложения - в справочной литературе).
(константы разложения - в справочной литературе).
Аналогичными преобразованиями уравнения, связывающего полный дифференциал энергии Гиббса с ее характеристическими параметрами, можно получить очень похожие выражения для уравнения Клапейрона-Клаузиуса применительно к равновесию жидкость ⇄ пар. Дополнительная особенность состоит лишь в том, что в дифференциальном виде для данного равновесия интерес представляет не только температурная зависимость давления насыщенного пара над жидкостью ( 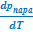 ), но и влияние внешнего давления на температуру кипения жидкости (
), но и влияние внешнего давления на температуру кипения жидкости ( 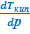 ):
):
ΔНисп ≈ ТиспVп 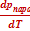 и
и 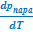 ≈
≈ 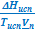 и
и 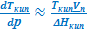 . (УрКл-Кл_2-диф)
. (УрКл-Кл_2-диф)
При выводе этих формул было использовано условие Vп ≫ Vт. После замены 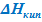 на λкип, получим:
на λкип, получим:
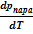 ≈
≈ 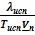 и
и 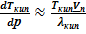 .
.
Линия равновесия жидкость ⇄ пар на фазовой p-T-диаграмме начинается из точки В
(см. рис.5.3), которая, как показано ранее, соответствует максимальной температуре, при которой еще сохраняется равновесие твёрдое тело ⇄ пар. Поскольку в выражении УрКл-Кл_2-диф 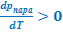 (
( 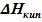 =
= 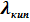 - положительная величина) - линия данного фазового равновесия также, как и линия равновесия твёрдое тело ⇄ пар имеет положительный угловой коэффициент. Кривизна её определяется второй производной
- положительная величина) - линия данного фазового равновесия также, как и линия равновесия твёрдое тело ⇄ пар имеет положительный угловой коэффициент. Кривизна её определяется второй производной 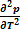 , которая в свою очередь определяется температурной зависимостью
, которая в свою очередь определяется температурной зависимостью 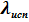 . Можно показать, что, как и для равновесия твёрдое тело ⇄ пар линия равновесия жидкость ⇄ пар обращена выпуклостью к оси температур. В то же время в общей точке В эти линии имеют разную величину наклона, разные значения угловых коэффициентов:
. Можно показать, что, как и для равновесия твёрдое тело ⇄ пар линия равновесия жидкость ⇄ пар обращена выпуклостью к оси температур. В то же время в общей точке В эти линии имеют разную величину наклона, разные значения угловых коэффициентов:
·  для равновесия т⇄п угловой коэффициент равен
для равновесия т⇄п угловой коэффициент равен 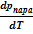 ≈
≈ 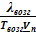 ;
;
· для равновесия ж⇄п угловой коэффициент равен 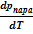 ≈
≈ 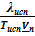 .
.
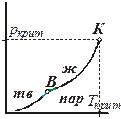
 В точке В для этих выражений совпадают и температуры, и мольный объем равновесной паровой фазы. В то же время, очевидно, что λвозг > λисп, поэтому кривая возгонки подходит к точке Вс большим наклоном, чем кривая испарения из нее выходит (рис. 5.5):
В точке В для этих выражений совпадают и температуры, и мольный объем равновесной паровой фазы. В то же время, очевидно, что λвозг > λисп, поэтому кривая возгонки подходит к точке Вс большим наклоном, чем кривая испарения из нее выходит (рис. 5.5):
Еще одной важной особенностью кривой равновесия жидкость ⇄ пар является то, что она обрывается в точке К, которая соответствует критическому состоянию вещества. Наличие такой точки на линии равновесия жидкость ⇄ пар является отражением того факта, что структура этих фаз не отличается принципиально. В жидкой фазе структурные единицы (молекулы, ионы или атомы) менее подвижны, лучше связаны, чем в газовой. Но в обеих фазах отсутствует дальний порядок, расположение частиц в целом хаотично. При нагревании растет внутренняя энергия, хаотичность в распределении частиц (энтропия). При этом различие между жидкостью и паровой фазой уменьшаются. В итоге при критических условиях (ркрит, Ткрит) обе фазы оказываются тождественными: становится одинаковой плотность, а значит и мольные объемы, а, следовательно, и энтропии "жидкости" и "пара". Равенство мольных объемов и энтропий равновесных фаз означает, что при выводе уравнения Клапейрона-Клаузиуса в выражении Sп - Sж = (Vп - Vж) 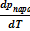 равенство достигается за счет того, что обе скобки равны нулю. Дальнейшее его преобразование теряет смысл. Это означает, что при критических и, тем более, при сверхкритических условиях к такой системе уравнение Клапейрона-Клаузиуса неприменимо.
равенство достигается за счет того, что обе скобки равны нулю. Дальнейшее его преобразование теряет смысл. Это означает, что при критических и, тем более, при сверхкритических условиях к такой системе уравнение Клапейрона-Клаузиуса неприменимо.
Описание равновесия твёрдое тело ⇄ жидкость начнем с кратких комментариев к положению соответствующей межфазной границы на диаграмме состояния.
· Не будем тратить много времени на строгое доказательство, что она должна выходить из точки пересечения линий равновесий твёрдое тело ⇄ пар и жидкость ⇄ пар.
· При выводе уравнения Клапейрона-Клаузиуса покажем, что угловой коэффициент линии равновесия твёрдое тело ⇄ жидкость может иметь разный знак, но практически всегда она располагается практически вертикально.
· Третье важное соображение основано на принципиальных отличиях твердых кристаллических фаз от жидкостей. Поэтому физические свойства данных фаз, их термодинамические характеристики при любых условиях будут существенно отличаться, следовательно, соответствующая межфазная граница не должна обрываться. Особые критические состояния вещества на этой границе не обнаруживаются.
Пусть мы имеем в состоянии равновесия 1моль твердого вещества и 1моль жидкости. Состояние равновесия означает, что Gт = Gж. Увеличением температуры (на произвольную величину dT) и одновременным увеличением давления (на конкретную величину dp) переведем систему в новое равновесие:
Gт + dGт = Gж + dGж,
что означает выполнение равенства dGт = dGп.
Учитывая, что энергия Гиббса является характеристической функцией от давления и температуры, получаем:
Vтdp ‒ SтdT = Vжdp ‒ SжdT.
После перегруппировки имеем: (Sж - Sт) 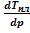 = (Vж - Vт). (V.3)
= (Vж - Vт). (V.3)
Обращаю внимание, что в данном случае интерес представляет именно влияние давления на температуру плавления, т.е. 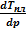 .
.
Слева имеем ΔSпл = Sж - Sт. По II-му началу термодинамики можем заменить эту разность на приведенную теплоту этого процесса: 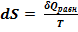 или в нашем случае для изобарно-изотермических условий ΔSпл =
или в нашем случае для изобарно-изотермических условий ΔSпл = 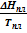 . Сразу заменим обозначение молярной теплоты плавления: ΔSпл =
. Сразу заменим обозначение молярной теплоты плавления: ΔSпл = 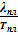 .
.
После подстановки в (V.3)и небольшого преобразования можем получить выражения для оценки теплоты плавления и, что более важно, для анализа барической зависимости температуры плавления:
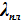 = Тпл(Vж - Vт)
= Тпл(Vж - Vт) 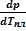 и
и 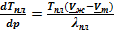 . (УрКл-Кл_3-диф)
. (УрКл-Кл_3-диф)
Дальнейшее преобразование, упрощение полученных равенств невозможно, поскольку молярные объемы твердой и жидкой фаз сопоставимы. Это означает, что Vж - Vт ≈ 0, следовательно, 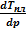 также устремляется к нулю, т.е. даже сильное изменение давление, обычно мало влияет на температуру плавления. Это возможно, если линия равновесия твёрдое тело ⇄ жидкость располагается на
также устремляется к нулю, т.е. даже сильное изменение давление, обычно мало влияет на температуру плавления. Это возможно, если линия равновесия твёрдое тело ⇄ жидкость располагается на
р-T-диаграмме практические вертикально. Что касается ее наклона, то знак 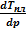 определяетсясоотношением между молярными объемами равновесных фаз. Обычно
определяетсясоотношением между молярными объемами равновесных фаз. Обычно 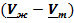 ≳ 0 (нормальные вещества), тогда и
≳ 0 (нормальные вещества), тогда и 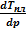 ≳0, линия наклонена вправо. Обратная ситуация наблюдается у веществ с аномальным поведением
≳0, линия наклонена вправо. Обратная ситуация наблюдается у веществ с аномальным поведением 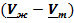 ≲ 0 и
≲ 0 и 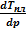 ≲0. В этом случае увеличение давления уменьшает температуру плавления. Такая ситуация наблюдается, например, у воды, висмута и некоторых других веществ (рис.5.6):
≲0. В этом случае увеличение давления уменьшает температуру плавления. Такая ситуация наблюдается, например, у воды, висмута и некоторых других веществ (рис.5.6):
Для равновесия твёрдое тело(1)⇄ твёрдое тело(2) вывод и полнота преобразования уравнения Клапейрона-Клаузиуса полностью аналогична только что разобранному случаю. Приведу только окончательное выражение в дифференциальной форме:
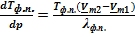 . (УрКл-Кл_4-диф)
. (УрКл-Кл_4-диф)
Но в отличие от формулы (УрКл-Кл_3-диф) в данном случае ситуация еще более неопределенная, поскольку нельзя заранее предсказать не только знак разности 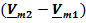 , но и знак энтальпии (теплоты) фазового перехода между двумя кристаллическими модификациями. Поэтому соответствующая межфазная граница может иметь очень разные угловые коэффициенты и по знаку, и по абсолютной величине.
, но и знак энтальпии (теплоты) фазового перехода между двумя кристаллическими модификациями. Поэтому соответствующая межфазная граница может иметь очень разные угловые коэффициенты и по знаку, и по абсолютной величине.
Обобщим полученные результаты:
| твердое тело ⇄ пар (возгонка) | жидкость ⇄ пар (испарение) | твёрдое тело ⇄ жидкость (плавление) | твёрдое тело(1)⇄ твёрдое тело(2) (структурный переход) |
| Дифференциальные формы уравнений Клапейрона-Клаузиуса | |||
ΔНвозг ≈ ТвозгVп 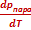 | ΔНисп ≈ ТиспVп 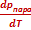 | ΔНпл = Тпл(Vж - Vт)  | ΔНф.п. = Тф.п.(Vт2 - Vт1)  |
 ≈ ≈ 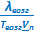 |  ≈ ≈ 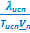 и и 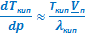 | 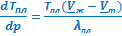 | 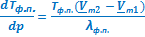 |
| Кроме того, включу в таблицу полученные выше дифференциальные выражения, позволяющие анализировать парциальное давление паровой фазы в равновесиях возгонки и испарения: | |||
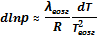 | 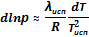 | ||
| Они оказываются необходимы для строгого, количественного описания некоторых фазовых равновесий в двухкомпонентных системах (Уравнение Шредера). | |||
| Интегральные формы уравнений Клапейрона-Клаузиуса | |||
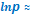 - - 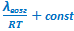 | 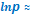 - - 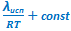 | ||
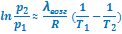 | 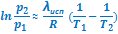 |
