Алгоритм решения уравнения в полных дифференциалах 4 страница
Точки, в которых частные производные равны нулю, называются стационарными точками. Стационарные точки и точки, в которых производные не существуют и которые лежат внутри области определения функции, называются критическими точками. Не всякая критическая точка является точкой экстремума.
Достаточное условие существования экстремума:
Пусть М0 (х0; у0) стационарная точка функции z = ƒ (х; у). Обозначим 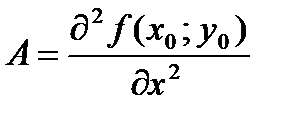 ,
, 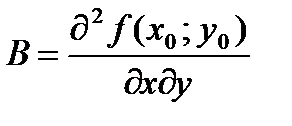 ,
, 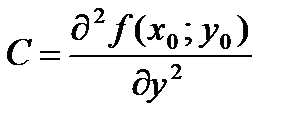 и составим дискриминант
и составим дискриминант 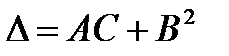 . Тогда:
. Тогда:
если Δ > 0, то функция имеет в точке M0 экстремум, а именно максимум, при A < 0 (или C < 0) и минимум, при A > 0 (или C > 0);
если Δ < 0, то в точке M0 экстремума нет;
если Δ = 0, то требуется дальнейшее исследование (сомнительный случай).
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Найти полный дифференциал функции 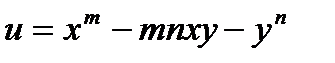 ;
;
2. Найти производную в точке М (n, m) по направлению 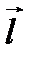 , образующего угол 450 с осью Ox, функции
, образующего угол 450 с осью Ox, функции 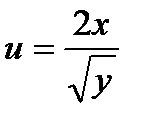 . Чему равен |grad u(M)|?
. Чему равен |grad u(M)|?
3. Найти производные второго порядка функции 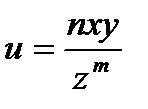 ;
;
4. Найти уравнение касательной плоскости и нормали гиперболического параболоида 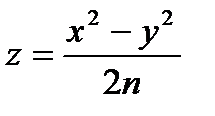 в точке
в точке 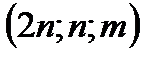 .
.
5. Найти экстремумы функции 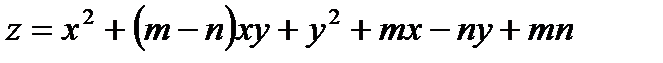 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Функция нескольких переменных.
2. Частные производные и полный дифференциал.
3. Производная функции нескольких переменных по направлению.
4. Градиент и его модуль.
5. Производная функции нескольких переменных высших порядков.
6. Уравнение касательной плоскости и нормали к поверхности.
7. Экстремумы функции нескольких переменных.
8.
Практическая работа №11
Тема: Нахождение неопределенного интеграла.
Цель: Научиться находить неопределенный интеграл функции разными методами интегрирования.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение.Функция F(x) называется первообразной для функции f(x), если F'(x)=f(x), или dF(x)=f(x)dx. Неопределенным интегралом от функции f(x) называется совокупность всех ее первообразных: 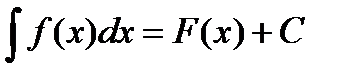 , где С – постоянная.
, где С – постоянная.
Отыскание неопределенного интеграла называется интегрированием функций. Правила интегрирования:
1) 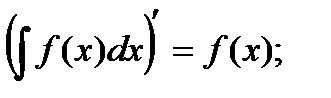 2)
2) 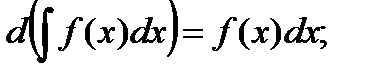 3)
3) 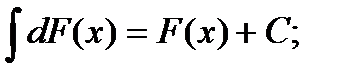
4) 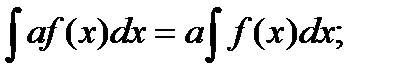 5)
5) 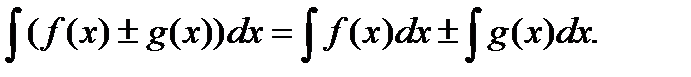
Таблица интегралов.
1. 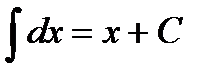 .
.
2. 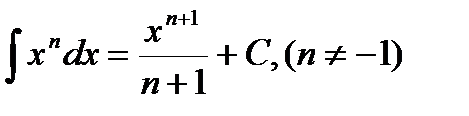 .
.
3. 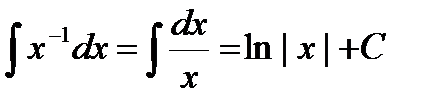 .
.
4. 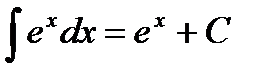 .
.
5. 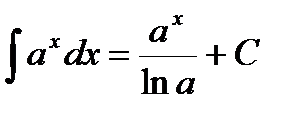 .
.
6. 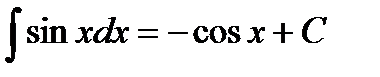 .
.
7. 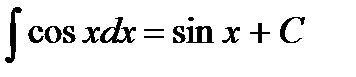 .
.
8. 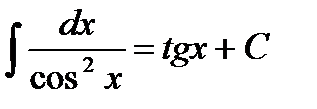 .
.
9. 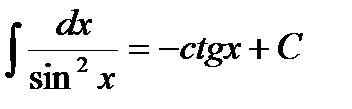 .
.
10. 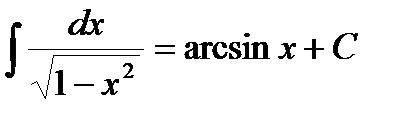 .
.
11. 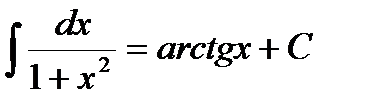 .
.
Замена переменных в неопределенном интеграле.
Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 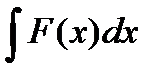 . Сделаем подстановку
. Сделаем подстановку 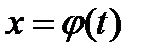 , где
, где 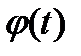 – функция, имеющая непрерывную производную.
– функция, имеющая непрерывную производную.
Тогда 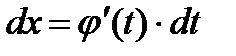 и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
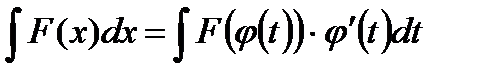
Интегрирование по частям
Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы для:
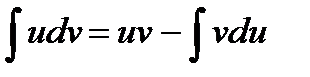
Интегрирование тригонометрических функций.
Интегрирование выражений вида 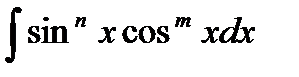 .
.
Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.
Интегрирование рациональных функций.
Известно, что многочлен n-й степени в общем случае имеет n комплексно-сопряжённых корней (некоторые корни могут совпадать). Соответственно, любой многочлен может быть разложен по формуле
 , где x1, x2,… xn – корни многочлена.
, где x1, x2,… xn – корни многочлена.
Следовательно, дробь, знаменателем которой является многочлен, может быть разложена следующим образом:
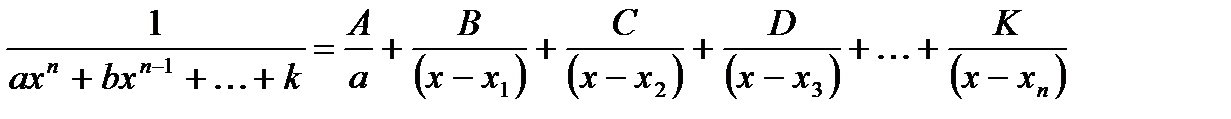 .
.
Эта операция разложения дроби в некотором смысле обратна операции приведения дробей общему знаменателю, с той разницей, что здесь ставится обратная задача - не привести дроби к общему знаменателю, а разложить дробь, имеющую общий знаменатель, на несколько дробей, имеющих разные знаменатели.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
Найти интегралы:
1) 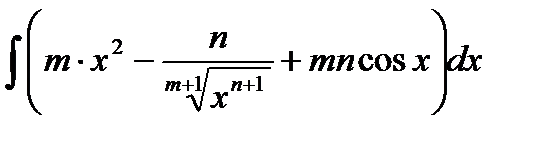 ;
;
2) 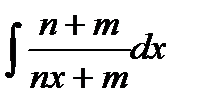 ;
;
3) 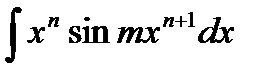 ;
;
4) 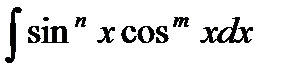 ;
;
5) 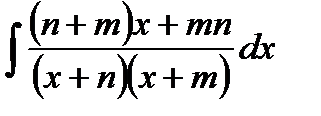 .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Первообразная функции. Свойства. Таблица.
2. Неопределенный интеграл, его свойства. Таблица.
3. Способ подстановки для интегрирования неопределённого интеграла.
4. Способ интегрирования по частям.
5. Интегрирование простейших рациональных дробей.
Практическая работа №12
Тема: Применение определенного интеграла.
Цель: Научиться находить площадь криволинейной трапеции и поверхности вращения,объем тела вращения, длину кривой. Научиться исследовать на сходимость несобственного интеграл.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определенный интеграл от функции f(x) на отрезке [a, b] с неопределенным связывает формула Ньютона–Лейбница:
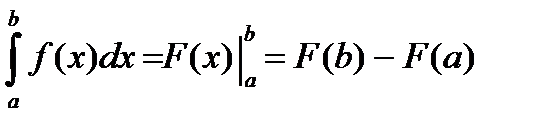
Основные свойства определенного интеграла:
1) 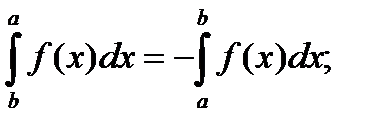
2) 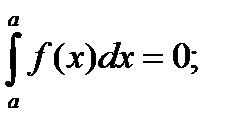
3) 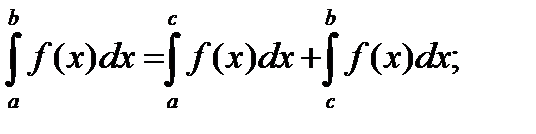
4) 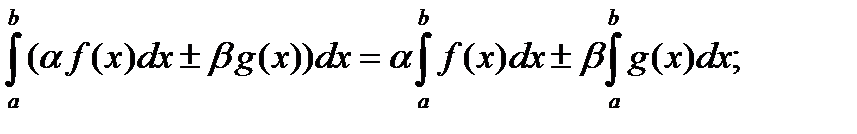
5) если 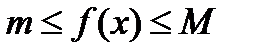 на [a,b], то m(b–a)<
на [a,b], то m(b–a)< 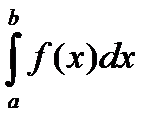 <M(b–a).
<M(b–a).
Понятие определенного интеграла широко применяется для вычисления различных геометрических и физических величин.
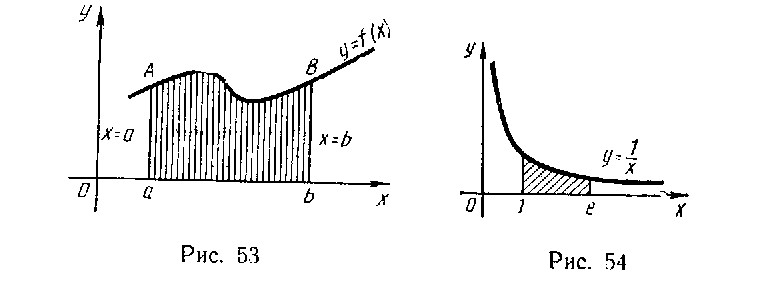 Площадь плоских фигур.
Площадь плоских фигур.
Площадь криволинейной трапеции аАВb, ограниченной графиком непрерывной функции у = f(x) (где а 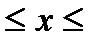 b), отрезком ab оси Оx: и отрезками прямых х=а и х = b, вычисляется по формуле
b), отрезком ab оси Оx: и отрезками прямых х=а и х = b, вычисляется по формуле 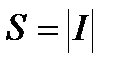 , где
, где 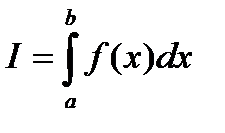 .
.
 Объем тела вращения.
Объем тела вращения.
Объем тела, образованного вращением вокруг оси Ох криволинейной трапеции аAВb, ограниченной непрерывной кривой у=f(х) (где а 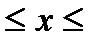 b ), отрезком аb оси Ох и отрезками прямых х = а и х=b, вычисляется по формуле
b ), отрезком аb оси Ох и отрезками прямых х = а и х=b, вычисляется по формуле 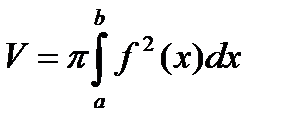 .
.
Путь, пройденный точкой.
Если точка движется прямолинейно и ее скорость v=f(t) есть известная функция времени t, то путь, пройденный точкой за промежуток времени 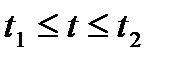 вычисляется по формуле
вычисляется по формуле
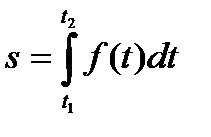 .
.
Длина дуги кривой
Пусть некоторая функция f(х) непрерывна на отрезке [a, b], и её график на данном промежутке представляет собой дугу кривой. Длина дугу кривой выражается формулой:
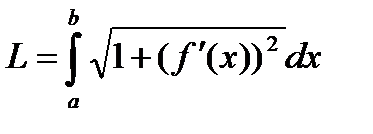 или если функция задана параметрически:
или если функция задана параметрически: 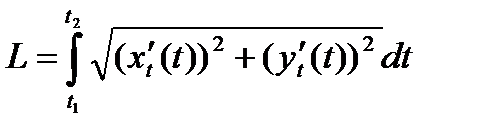 .
.
Несобственный интеграл.
В общем виде несобственные интегралы с бесконечными пределами выглядят так:
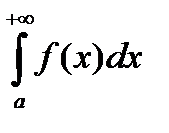 или
или 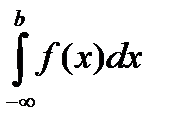 или
или 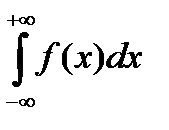 .
.
Рассмотрим случай 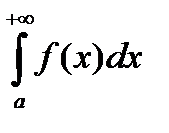 . Техника работы с другими разновидностями – аналогична.
. Техника работы с другими разновидностями – аналогична.
Применим формулу Ньютона-Лейбница при условии что 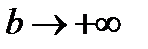 :
:
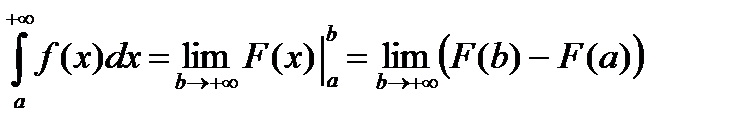 .
.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1. Вычислить: 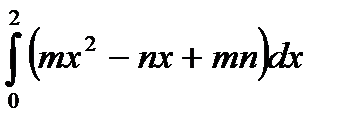
2. Построить схематический чертеж и найти площадь фигуры, ограниченной линиями:
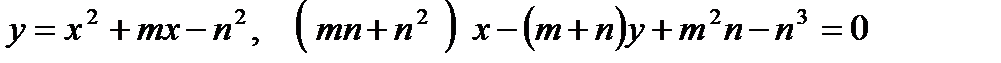 .
.
3. Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями:
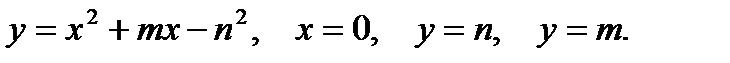
4. Скорость движения точки изменяется по закону v = t2 + nt +m (м/с). Найти путь S, пройденный точкой за (nm) секунд от начала движения.
5. Найдите длину кривой 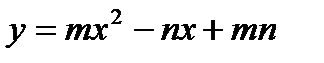 от точки х0=1 до точки х1=2.
от точки х0=1 до точки х1=2.
6. Исследовать на сходимость 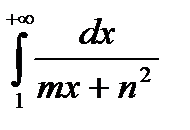
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Определённый интеграл.
2. Его свойства.
3. Геометрический и физический смысл определённого интеграла.
4. Несобственный интеграл.
Практическая работа №13
Тема: Нахождение площадь поверхности и объема тела.
Цель: Научиться вычислять двойной, тройной и поверхностный интеграл и находить объем тела.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Двойной интеграл
Двойной интеграл в общем виде записывается следующим образом: 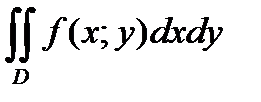 ,
,
где D – область интегрирования (плоская фигура);
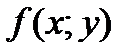 – подынтегральная функция двух переменных, часто она довольно простая.
– подынтегральная функция двух переменных, часто она довольно простая.
Для того чтобы вычислить двойной интеграл, его необходимо свести к так называемым повторным интегралам:
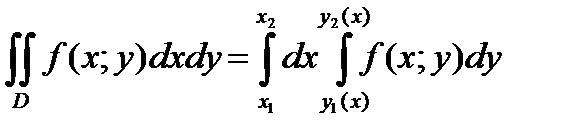 ,
,
где 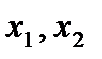 - границы плоской фигуры D с лева и права вдоль оси Ox;
- границы плоской фигуры D с лева и права вдоль оси Ox;
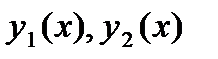 - функции ограничивающие плоскую фигуру D с низу и верху вдоль оси Oy.
- функции ограничивающие плоскую фигуру D с низу и верху вдоль оси Oy.
Порядок обхода области интегрирования D можно изменить:
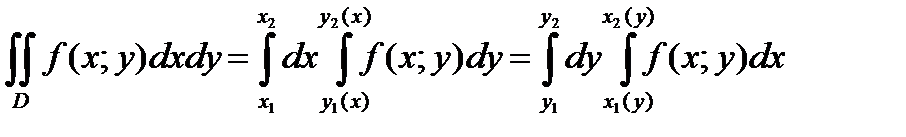 .
.
Площадь плоских фигур.
Вычислим площадь плоской фигуры D, ограниченной линиями x=a, x=b, y=f(x), y=g(x). Для определённости считаем, что f(x)>g(x) на отрезке [a; b]. Площадь данной фигуры численно равна:
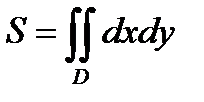 ,
,
когда под интегральная функция двух переменных равна единице 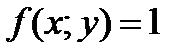 .
.
Изобразим область D на чертеже:
Выберем первый способ обхода области: g(x) ≤ y ≤ f(x) и a ≤ x ≤ b.
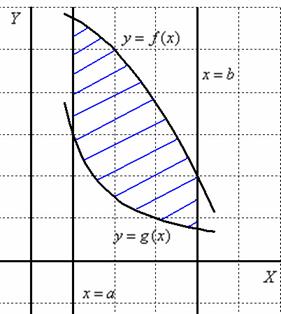 Таким образом:
Таким образом: 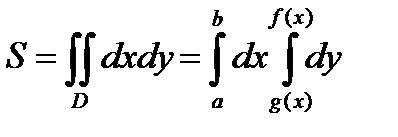 .
.
Повторные интегралы можно считать по отдельности. Сначала внутренний интеграл, затем – внешний интеграл.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
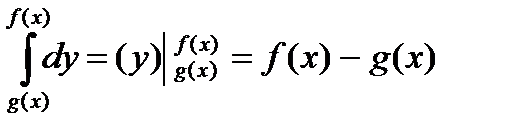 .
.
Используется формула Ньютона-Лейбница, с той лишь разницей, что пределами интегрирования являются не числа, а функции.
2) Результат, полученный в первом пункте необходимо подставить во внешний интеграл: 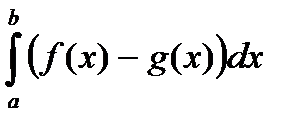 .
.
В полярных координатах, таким образом: 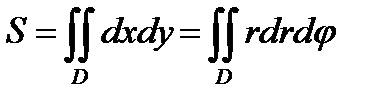 .
.
Объем тела
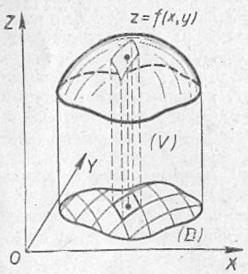 Предполагаем, что функция
Предполагаем, что функция 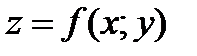 существует в каждой точке
существует в каждой точке 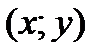 плоской области D и задаёт некоторую поверхность трехмерного пространства. Для определенности считаем, что
плоской области D и задаёт некоторую поверхность трехмерного пространства. Для определенности считаем, что 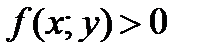 , то есть поверхность располагается над плоскостью XOY.
, то есть поверхность располагается над плоскостью XOY.
Согласно общей концепции интегрирования, произведение 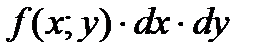 равно бесконечно малому объёму dV элементарного кусочка тела (посмотрите на кусок, выделенный на чертеже пунктирными линиями, и мысленно сделайте бесконечно малыми его «длину» и «ширину»). Двойной же интеграл объединяетэти бесконечномалые значения dV по всей области D, в результате чего мы получаем суммарный (интегральный) объём всего цилиндрическогобруса
равно бесконечно малому объёму dV элементарного кусочка тела (посмотрите на кусок, выделенный на чертеже пунктирными линиями, и мысленно сделайте бесконечно малыми его «длину» и «ширину»). Двойной же интеграл объединяетэти бесконечномалые значения dV по всей области D, в результате чего мы получаем суммарный (интегральный) объём всего цилиндрическогобруса 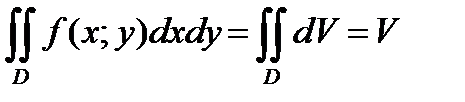 .
.
Тройной интеграл
В простейшем случае, когда 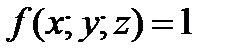 , тройной интеграл
, тройной интеграл 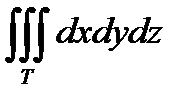 численно равен объёму тела T. И действительно, в соответствии с общим смыслом интегрирования, произведение
численно равен объёму тела T. И действительно, в соответствии с общим смыслом интегрирования, произведение 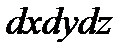 равно бесконечно малому объёму dV элементарного «кирпичика» тела. А тройной интеграл как раз и объединяет все эти бесконечно малые частички по области T, в результате чего получается интегральное (суммарное) значение объёма тела:
равно бесконечно малому объёму dV элементарного «кирпичика» тела. А тройной интеграл как раз и объединяет все эти бесконечно малые частички по области T, в результате чего получается интегральное (суммарное) значение объёма тела: 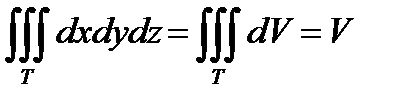 .
.
ВАРИАНТЫ
Числовых данных параметров т и п определяются по первым буквам фамилии и полного имени.
| А-В | Г-Е | Ж-И | К-М | Н-П | Р-Т | У-Х | Ц-Ш | Щ-Э | Ю-Я | ||
| Фамилия | т | ||||||||||
| Имя | п |
ЗАДАНИЯ
1) Заменить порядок интегрирования и вычислить повторный интеграл 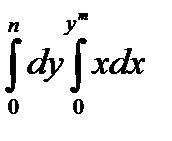 .
.
2) Вычислить площади двойным интегралом ограниченные линиями 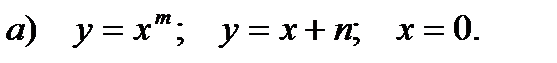
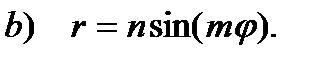
3) Вычислить объем тела, ограниченного поверхностями: 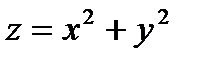 ,
, 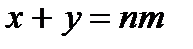 ,
, 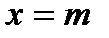 ,
, 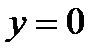 ,
, 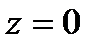 .
.
4) Вычислить объем тела, ограниченного поверхностями: 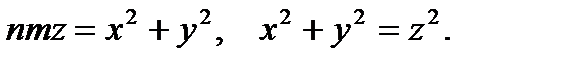
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с теоретическими сведениями.
2. Выбрать свой вариант согласно первым буквам фамилии и полного имени.
3. Записать исходные данные.
4. Решить задания.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Двойной интеграл. Свойства. Вычисление площади, объема и поверхности.
2. Тройной интеграл. Свойства. Вычисление объема.
Практическая работа №14
Тема: Решение дифференциальных уравнений первого порядка.
Цель: Научиться решать дифференциальные уравнения первого порядка.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Определение. Дифференциальным уравнениемназывается уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Определение. Общим решениемдифференциального уравнения называется такая дифференцируемая функция y = j(x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
Определение. Решение вида у = j(х, С0) называется частным решениемдифференциального уравнения.
Определение. Дифференциальным уравнением первого порядканазывается соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
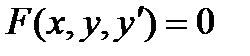
Дифференциальные уравнения с разделяющимися переменными.
Общий вид такого уравнения
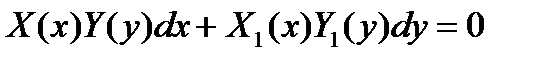 ,
,
где Х(х), Х1(х) — функции только от х, У(у), У1 (у) — функции только от у.
Поделив обе части уравнения на произведение Х1(х)У(у) 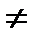 0, получим уравнение с разделенными переменными
0, получим уравнение с разделенными переменными
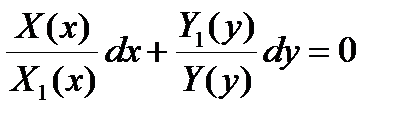 .
.
Общий интеграл этого уравнения имеет вид
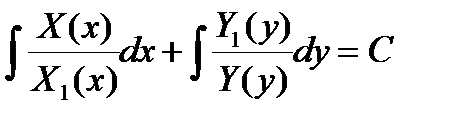 .
.
Замечание. Если произведение Х1 (х) У(у) =0 при х=а и у=b, то эти функции х=а и у=b являются решениями дифференциального уравнения при условии, что при этих значениях х и у уравнение не теряет числового смысла. Геометрически эти решения представляют собой прямые, параллельные осям координат.
Однородное дифференциальное уравнение
Однородное дифференциальное уравнение можно записать в виде 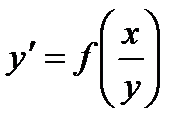 .
.
Абсолютно все однородные уравнения можно решить с помощью одной-единственной стандартной замены 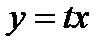 .
.
Подставляем 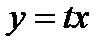 и
и 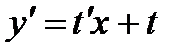 в исходное уравнение
в исходное уравнение 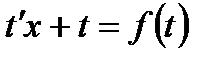 , заметим, что теперь уравнение имеет вид с разделяющимися переменными.
, заметим, что теперь уравнение имеет вид с разделяющимися переменными.
После нахождения 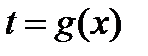 , ответ подаем в виде
, ответ подаем в виде 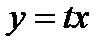 .
.
Линейные дифференциальные уравнения первого порядка.
Общий вид такого уравнения
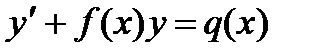 , (1)
, (1)
где f(x) и q(x) – заданные функции от х. Это уравнение является линейным относительно искомой функции и ее производной.
Есди q(x)=0, то линейное дифференциальное уравнение (1) называется однородным. Оно имеет вид 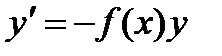 и решается методом разделения переменных.
и решается методом разделения переменных.
Еслн f(x)=0, то уравнение (1) принимает вид у'=q(x) и решается методом разделения переменных.
Существуют различные приемы решения линейного неоднородного дифференциального уравнения. Рассмотрим два из них.
1. Этот прием решения основан на применении следующей теоремы: если у=φ(х) - некоторое решение уравнения (1), то все решения этого уравнения задаются формулой
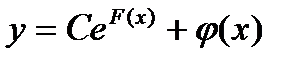 ,
,
где СеF(x) — общее решение однородного уравнения. Иными словами, для нахождения общего решения уравнения (1) достаточно найти хотя бы одно его частное решение,
2. Этот прием решения основан на простом замечании, что любую величину t (переменную или постоянную) можно представить в виде произведения двух множителей: t = uv, причем один из них можно выбрать произвольно (лишь бы он был отличен от нуля).
Решение линейного неоднородного дифференциального уравнения будем искать в виде у = uv, где u и v — функции от х. Подставляем в уравнение у = uv и у' = u`v+v`u.
