Скорость изменения импульса тела равна векторной сумме всех действующих на него сил. 3 страница

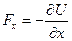. (42)

Здесь вместо символов d использованы символы 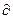для обозначения частных производных. Это значит, что во время дифференцирования функции U(x,y,z,) по одной из координат, с остальными координатами обращаются как с константами.

Кинетическая энергия частицы. Теорема о кинетической энергии. Рассмотрим частицу, движущуюся под действием некоторой силы, равной по второму закону Ньютона 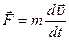. При перемещении 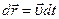элементарная работа этой силы .

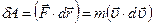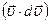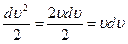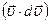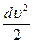Поскольку =udu, где du - приращение модуля скорости, а , то = , Þ 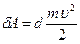. Отсюда видно, что работа силы 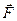идет на приращение величины 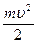. Эта величина называется кинетической энергией:

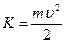. (43)

Проинтегрируем выражение 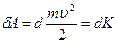: Þ 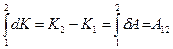. И окончательно

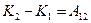. (44)

Мы доказали теорему о кинетической энергии:

Приращение кинетической энергии частицы на перемещении из точки 1 в точку 2 равно алгебраической сумме работ всех сил, действующих на частицу на том же перемещении. Очень рекомендую использовать именно эту теорему вместо закона сохранения энергии в случаях, когда в задаче имеется единственная частица.

Кинетическая энергия системы частиц. Определим кинетическую энергию системы частиц как сумму кинетических энергий всех составляющих систему частиц:

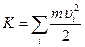. (45)

Опишем состояние системы в некоторый момент времени как совокупность положений всех её частиц. Пусть в течение некоторого времени i-я частица системы переместилась из точки i₁в точку i₂. По теореме о кинетической энергии: 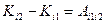, где 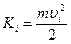. Поскольку каждая частица системы могла за это время переместиться в новое положение, то изменилось и состояние системы в целом: система перешла из состояния 1 в состояние 2. Просуммируем изменения кинетической энергии всех частиц системы, тогда изменение кинетической энергии при переходе из состояния 1 в состояние 2 равно сумме работ всех сил, действующих на частицы системы – внешних и внутренних, как потенциальных, так и непотенциальных:

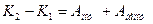. (46)

Механическая энергия. Согласно определению потенциальной энергии, работа потенциальных сил равна убыли потенциальной энергии в начальном и конечном состояниях: 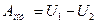. Таким образом, 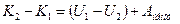, Þ

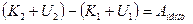. (47)

Выражение в круглых скобках называется полной механической энергией системы, или просто механической энергией. Механическая энергия системы равна сумме её кинетической и потенциальной энергий:

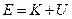. (48)

Выражение (47) можно переписать:

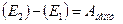. (49)

Мы получили закон изменения механической энергии: изменение механической энергии системы равно работе всех непотенциальных сил (как внешних, так и внутренних).

Закон сохранения энергии в механике. Если непотенциальных сил нет, или их работа равна нулю, то очевидно, 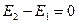, откуда следует закон сохранения энергии в механике:

в отсутствие непотенциальных сил полная механическая энергия изолированной (или находящейся во внешнем потенциальном поле) системы сохраняется.

Обратите внимание! 1 Мы неявно предположили, что работу всех потенциальных сил мы «упаковали» в виде потенциальной энергии. Потенциальная энергия системы в общем случае включает в себя потенциальную энергию взаимодействия частиц системы и потенциальную энергию системы во внешнем потенциальном поле (если оно есть). В некоторых случаях работу внешних потенциальных сил бывает удобно не включать в изменение потенциальной энергии системы и тогда потенциальная энергия состоит только из энергии взаимодействия составляющих её частиц. В этом случае закон изменения энергии в механике следует формулировать иначе: изменение механической энергии системы равно суммарной работе всех внешних сил (потенциальных и непотенциальных) и непотенциальных внутренних сил.

2 В применении этого закона есть тонкости, которые не очевидны из данных выше формулировок. Если наша система состоит из обычных тел (камни, кирпичи, бруски на наклонной плоскости, шарики и т.п.), то силой гравитационного притяжения между ними можно пренебречь из-за её малости, зато потенциальную энергию во внешнем гравитационном поле (Земли) всегда включают в потенциальную энергию системы. Если при этом «на тело действует сила », то обычно студент не понимает, куда включать её работу? С одной стороны, она вроде бы внешняя, Þ не следует включать ее работу в потенциальную энергию; с другой стороны она, как правило, потенциальная (в частности, постоянная), поэтому - надо включать? Совет: не включайте и тогда используйте закон изменения энергии в механике в форме: изменение механической энергии системы равно суммарной работе всех внешних и непотенциальных внутренних сил

Применение законов сохранения к задаче о столкновениях шаров. Существует большое количество задач, связанное с двумя типами столкновений: упругие и неупругие. Обратите внимание! В этом разделе для компактности векторы обозначены жирным шрифтом, как в учебниках.

При абсолютно упругомударе выполняются

1. Закон сохранения импульса (ЗСИ), 2. Закон сохранения энергии (ЗСЭ).Пусть скорости тел равны до столкновения v₁ и v₂ , после - u₁ и u₂ . Если удар центральный, то векторы v₁ , v₂ , u₁ и u₂ лежат на одной прямой! Запишем оба закона сохранения (ЗСЭ умножим на 2)

m₁ v₁ + m₂v₂ =m₁ u₁ + m₂u₂ (1)

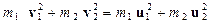. (2)

В обоих уравнениях перенесем все, что касается m₁ в левую часть, а m₂ - в правую. Заодно во втором уравнении представим разность квадратов скоростей как произведение их суммы на разность

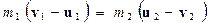(3)

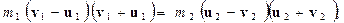(4)

Из сравнения уравнений (3) и (4) следует, что

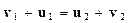. (5)

Умножим последнее уравнение на m₁и сложим с уравнением (1)

m₁ v₁ + m₁ u₁ + m₁ v₁ +m₂ v₂ =m₁ u₂ + m₁v₂ + m₁ u₁ + m₂u₂,

где после приведения подобных членов неизвестной останется только скорость u₂:

2 m₁ v₁ +m₂v₂ =m₁ u₂ + m₁v₂ + m₂ u₂,следовательно

.

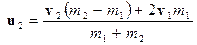Для нахождения u₁ уравнение (5) умножим на m₂ и вычтем из него уравнение (1). После приведения подобных членов аналогично получаем u₁:

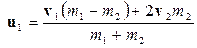
При абсолютно неупругом ударе выполняется только Закон сохранения импульса (ЗСИ).Закон сохранения энергии не выполняется, так как часть механической энергии переходит во внутреннюю за счет неупругой деформации. При этом после столкновения скорость у тел одинакова - они движутся как единое тело. В соответствии с законом сохранения импульса

m₁ v₁ + m₂v₂ = (m₁ + m₂)u,

откуда легко выразить скорость тел u после столкновения:

.

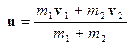Обратите внимание! В данных выводах все скорости представлены векторно. Поэтому в каждой конкретной задаче нужно сначала сделать рисунок, выбрать ось для проектирования, а затем спроектировать полученные здесь формулы на Вашу ось с учетом знаков проекций скоростей!

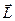Момент импульса частицы. Момент силы. Моментом импульса частицы А (рис.13) относительно точки О называется вектор , равный векторному произведению векторов 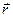и :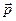

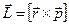, (50)

модуль которого равен L=rpsina=lp, (51)

где величина l, равная длине перпендикуляра, опущенного из точки О на линию вектора импульса l= rsina называется плечом вектора импульса .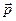

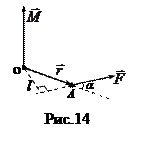Моментом силы относительно точки О называется вектор 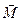, равный векторному произведению векторов 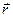и 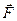(рис.14):

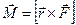. (52)

Уравнение моментов. Продифференцируем (50) по времени:

.

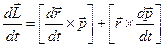Вектор скорости 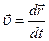совпадает по направлению с вектором 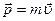, поэтому первое слагаемое равно нулю. Производная 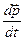= 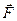по второму закону Ньютона, поэтому второе слагаемое представляет собой момент силы относительно точки О. Так мы приходим к уравнению моментов: производная по времени от момента импульса частицы относительно некоторой точки О равна моменту равнодействующей силы относительно той же точки О:

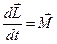. (53)

Из уравнения моментов (53) следует, что если 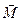= 0, то 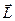=const. Другими словами, если момент всех сил, действующих на частицу, равен нулю, то момент импульса частицы относительно той же точки остается постоянным.

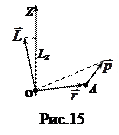Момент импульса и момент силы относительно оси. Пусть относительно некоторой точки О на неподвижной оси Z момент импульса частицы А равен 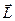, а момент сил, действующих на частицу, равен 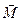(рис.15). Моментом импульса L_z

относительно оси Z называют проекцию вектора 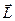на ось Z. Моментом силы M_z

относительно оси Z называют проекцию вектора 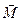на ось Z. Записав уравнение (53) в проекциях на ось Z, получим

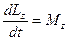. (54)

Производная по времени от проекции момента импульса частицы относительно некоторой оси Z равна проекции момента равнодействующей силы относительно той же оси.

Если момент силы относительно некоторой неподвижной оси равен нулю, то момент импульса относительно той же оси остается постоянным. Найдем выражения для L_z и M_z. Для этого удобно ввести цилиндрическую систему координат: r, j, z, связав с частицей А орты 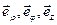, направленные в сторону возрастания соответствующих координат (рис.16). В этой системе радиус-вектор 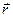и импульс 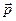частицы можно записать так ; .

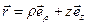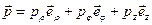Запишем векторное произведение в выражении момента импульса 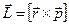в виде определителя матрицы 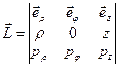, откуда видно, что проекция момента импульса на ось Z равна

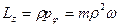, (55)

где r - расстояние частицы от оси Z; 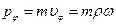, где w - проекция угловой скорости на ось Z. Аналогично запишем момент силы:

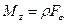. (56)

Закон сохранения момента импульса. Определим момент импульса системы частиц, как векторную сумму моментов импульсов её отдельных частиц:

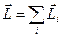, (57)

а суммарный момент сил, приложенный к системе, как 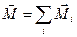, где все векторы определены относительно одной и той же точки О, лежащей на некоторой неподвижной оси 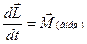. Продифференцируем выражение (57) по времени: 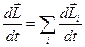. Производная 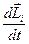равна моменту всех сил, действующих на i-ю частицу. Представим момент всех сил 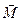как сумму моментов внутренних и внешних сил: 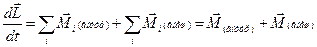. Суммарный момент всех внутренних сил относительно любой точки равен нулю. Действительно, силы взаимодействия между точками внутри системы - это силы взаимодействия между всеми парами точек. Две силы в каждой паре равны по модулю и противоположно направлены по третьему закону Ньютона. Поэтому и их моменты относительно любой точки равны по модулю и противоположно направлены. Следовательно, суммарный момент всех внутренних сил равен нулю. В результате последнее уравнение приобретает вид

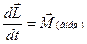. (58)

Это значит: производная момента импульса системы по времени равна суммарному моменту всех внешних сил. Из уравнения (58) следует, что приращение момента импульса системы за конечный промежуток времени t

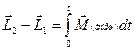. (59)

Это значит: приращение момента импульса системы равно импульсу суммарного момента всех внешних сил. Отсюда непосредственно вытекает

Закон сохранения момента импульса. Действительно, для изолированной (замкнутой) системы внешних сил нет, следовательно, правая часть в выражении (59) равна нулю. И тогда момент импульса замкнутой системы частиц остается постоянным: 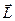=const. В более частном случае у незамкнутых систем может сохраняться не сам момент импульса, а его проекция на некоторую неподвижную ось. Это бывает тогда, когда проекция суммарного момента всех внешних сил на эту ось равна нулю. Действительно, проекция уравнения (58) на некоторую неподвижную ось Z выглядит так: 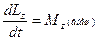. Если 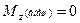, то .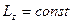

Вращение твердого тела вокруг неподвижной оси. Твердое тело можно представить как систему материальных точек. Тогда момент импульса относительно неподвижной оси Z согласно формуле (55), можно записать 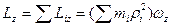, так как проекция угловой скорости у всех точек твердого тела одинакова. Введем обозначение 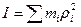, тогда

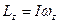. (60)

Величина 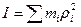, (61)

где m_i – масса i-й материальной точки, r_i – ее расстояние до оси вращения, называется моментом инерции твердого тела, который, очевидно, зависит от распределения масс m_i относительно оси вращения. Для вычисления момента инерции тела можно в формуле (61) перейти к пределу, тогда

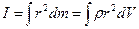, (62)

где dm и dV – масса и объем элемента тела, находящегося на расстоянии r от оси Z; r - в последней формуле плотность тела в dV.

Моменты инерции некоторых однородных твердых тел представлены в таблице.

Твердое тело	Ось Z	Момент инерции
Тонкий стержень длины l	Перпендикулярна стержню, проходит через середину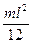
Тонкий стержень длины l	Перпендикулярна стержню, проходит через конец стержня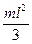
Сплошной цилиндр радиуса R	Совпадает с осью цилиндра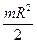
Тонкий диск радиуса R	Перпендикулярна диску, проходит через центр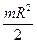
Тонкий диск радиуса R	Совпадает с диаметром диска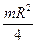
Шар радиуса R	Проходит через центр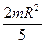

В некоторых случаях вычисление момента инерции значительно упрощается, если воспользоваться теоремой Штейнера:

момент инерции Iотносительно произвольной осиZравен моменту инерцииI_cотносительно осиZ_c, параллельной данной и проходящей через центр масс тела, плюс произведение массы тела на квадрат расстоянияaмежду осями:

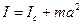. (63)

Таким образом, если известен момент инерции I_c , то нахождение момента инерции элементарно. Например, момент тонкого стержня длины l, относительно оси, перпендикулярной стержню и проходящей через его конец, равен

.

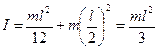Основное уравнение динамики вращения твердого тела. Запишем уравнение (58) в проекции на неподвижную ось Z:

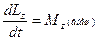. (64)

Поскольку 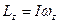и I постоянен для данного твердого тела, то, подставляя в (60), получим

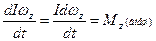, или

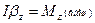. (65)

Кинетическая энергия вращающегося твердого тела относительно неподвижной оси.

Как мы уже упоминали, скорость i-й частицы твердого тела равна 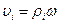, тогда кинетическую энергию тела можно записать как сумму кинетических энергий составляющих его частиц

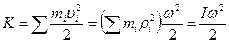. Таким образом, кинетическая энергия вращающегося тела

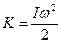. (66)

Работа внешних сил при вращении твердого тела вокруг неподвижной оси.

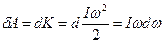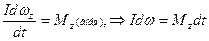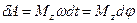В соответствии с (46) работа всех внешних сил, действующих на твердое тело, равна приращению только кинетической энергии тела, так как его потенциальная энергия при этом не меняется, Þ , где w - проекция угловой скорости на ось вращения (т.е. w=w_z). Так как , Þ 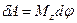, Þ , Þ

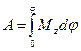. (67)

При 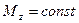, работа вычисляется ещё проще: А= 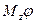. Если силы таковы, что их момент 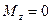, то работы они не производят.

Кинетическая энергия при плоском движении твердого тела. Примерами плоского движения твердого тела являются: шар, цилиндр или диск, катящийся по горизонтальной или наклонной плоскости и т.п. Можно показать, что при этом кинетическая энергия складывается из суммы кинетических энергий вращения вокруг оси симметрии, проходящей через центр масс, и поступательного движения центра масс:

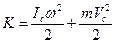. (68)

Здесь есть тонкости, о которых студент обычно не догадывается, поэтому и не допускает ошибок.

Колебания и волны

Гармонические колебания.

Гармоническими называются колебания, в которых величина х изменяется по закону

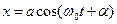, (1)

где а – амплитуда, 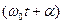- фаза, a - начальная фаза, w₀ - циклическая частота, w₀=2pn . Период колебаний T , а также частоты ν и w₀ связаны:

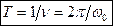. (2)

Обратите внимание на наименования единиц измерения: [w] = c^-1, [n]=Гц.

Продифференцировав (1) по времени, найдем скорость 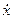и ускорение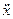

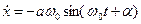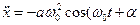; ). (3)

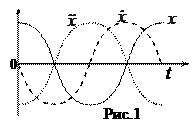Графики на рис.1 показывают, что х и 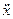находятся в противофазе, а скорость 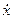опережает смещение х на .

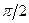Наиболее часто встречающее заблуждение состоит в том, что учащиеся думают, что на рис.1 изображена траектория. НЕТ! Это графики! Зависимости х (и производных) от времени! Притом при нулевой начальной фазе и одинаковых по масштабу амплитудах! Движение одномерное! Поэтому траектория – набор отрезков вдоль вертикальной оси х.