Существующие подходы к изучению структуры потока

Можно предложить разные подходы к изучению структуры потока и влияния этой структуры на ход химических процессов.

Наиболее полную информацию о структуре потока можно получить, зная скорость жидкости в любой точке аппарата, т. е. получив поле скоростей. В принципе это дает исчерпывающую картину потока. Точное описание поля скоростей может явиться материалом для решения любой задачи, относящейся к течению жидкости. Но при таком подходе встречаются труднопреодолимые препятствия.

Прежде всего, чрезвычайно трудна экспериментальная задача измерения скоростей во всех частях потока. В любом аппарате имеются области, где поток либо проходит сквозь сужения, либо резко заворачивает. Здесь почти невозможно измерить скорость, не нарушив структуру потока.

Более того, подобные эксперименты зачастую проводить нерационально из-за трудности обработки полученной таким путем информации о гидродинамической структуре потоков совместно с уравнениями переноса массы и энергии (для тепло- и массообменных процессов).

Поле скоростей — сложная трехмерная структура, описание которой должно содержать функции по меньшей мере трех переменных (координат). Нестационарность (например, в турбулентном потоке) добавляет четвертую — время. Математическое описание процесса обычно получается в виде систем дифференциальных уравнений в частных производных; решить такую систему даже с помощью вычислительных машин удается лишь в простейших случаях.

Второй возможный подход — выделить изо всей сложной картины потока одну характеристику и основывать описание на ней. Так, можно было бы описывать процесс перемешивания. Наиболее распространено описание потока на основе распределения времени пребывания.

Третий подход — построение упрощенных мысленных моделей потока. Упрощая сложную картину, такая модель в то же время должна отражать существенные для нас особенности потока — в первую очередь, с достаточной адекватностью описывать особенности протекания в данном потоке химических, тепловых и массообменных процессов.

Среднее время τ пребывания всех частиц потока жидкости в аппарате определяется простым соотношением

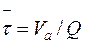(1)

где V_a - объем рабочей зоны аппарата, Q-объемный расход потока

Совокупную информацию о характере движения среды в аппарате содержит функция распределения частиц потока по времени пребывания. Разумеется, функция распределения времени пребывания является далеко не полной характеристикой движения, хотя и достаточной для интегральной оценки работы аппарата в тех случаях, когда степень превращения частиц определяется только временем их пребывания в нем. Кроме того, экспериментальные функции распределения времени пребывания могут оказаться полезными для проверки адекватности и определения параметров упрощенных теоретических моделей движения сред в аппаратах, называемых моделями гидродинамической структуры потоков.

Для того чтобы измерить случайную величину - время пребывания частицы потока в аппарате, необходимо пометить ее таким образом, чтобы метка позволяла зарегистрировать моменты входа и выхода частицы из аппарата, и получить кривую изменения концентрации в потоке на выходе. Эту кривую называют выходной кривой, или кривой отклика

Для получения кривых отклика используют установку, принципиальная схема которой представлена на рис. 2.

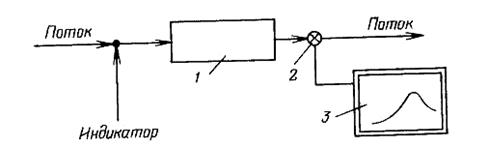
Рис 2 Схема установки для получения кривых отклика 1-аппарат, 2- концентратомер, 3 - графопостроитель

По одному методу в момент, принимаемый за начало τ, во входящий поток быстро (теоретически мгновенно) вводят индикатор, или трассер. По другому методу индикатор вводится ступенчато, т.е. в момент τ концентрация индикатора скачком возрастает до некоторой величины С₁ и остается на этом уровне длительное время. В качестве индикатора может быть использовано вещество, которое легко количественно определяется в жидкости и не реагирует ни с жидкостью, ни с материалом аппарата (например, к воде можно примешивать раствор красителя, неорганической соли, радиоактивные изотопы и т.д.). Количество индикатора должно быть небольшим, чтобы не оказывать влияния на характер потока. Затем измеряют концентрацию С индикатора в потоке, выходящем из аппарата, как функцию времени τ, т. е. отклик на входное возмущение получают в виде выходных кривых, или кривых отклика, которые часто называют С-кривыми. Знание С-кривых позволяет установить, сколько жидкости, какая часть ее от вошедшей в аппарат, выйдет из него через определенный промежуток времени.

В зависимости от способа ввода индикатора получают или дифференциальную функцию распределения С(τ) —при импульсном вводе индикатора, или интегральную функцию распределения F(τ) -при ступенчатом вводе индикатора. По виду полученных кривых отклика делают вывод о структуре потоков в аппарате.

При таком подходе вскрыть механизм происходящих в данном аппарате процессов затруднительно, поскольку реальное поле скоростей в нем неизвестно, т.е в этом случае аппарат рассматривается как «черный ящик». Вместе с тем такой метод анализа структуры потоков в аппарате достаточно прост, существенно упрощается количественная обработка полученных данных, так как получают функцию только одной переменной-времени.

Обозначим М_о количество индикатора, вводимого в поток, непрерывно входящий в аппарат, а c- концентрацию индикатора на выходе из аппарата. Начальная концентрация c₀ в аппарате, например, при условии полного перемешивания в нем жидкости будет определяться как отношение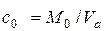

Чтобы иметь возможность распространить результаты анализа модельного потока на другие, подобные данному, введем безразмерные (приведенные) параметры: приведенное время 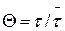; приведенная концентрация С = с/с₀ .

Рассмотрим произвольный текущий момент времени τ. За бесконечно малый промежуток времени из аппарата выйдет объем жидкости Qdτ, а количество индикатора dM, вышедшее с этим объемом жидкости,-

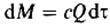
В безразмерных координатах:

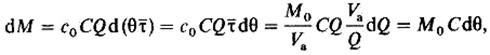
или

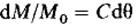
Таким образом, 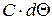равно доле первоначально введенного индикатора, который выходит из аппарата за промежуток времени 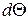. По определению плотности вероятности случайной величины

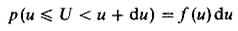
вероятность того, что случайная величина U примет какое-либо значение в интервале от и до и + du, равна плотности вероятности, или дифференциальной функции распределения, этой величины (здесь р- символ вероятности; U - обозначение случайной величины, могущей принимать разные значения; u - какое-либо конкретное ее значение). Таким образом, безразмерная концентрация индикатора С равна плотности вероятности (дифференциальной функции распределения) безразмерного времени .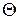

Если ввод индикатора осуществить ступенчато, получим F-кривую отклика, т.е. интегральную функцию распределения, причем

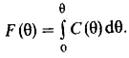
При θ <0 С(θ) = 0, т.е. вероятность того, что частица выйдет из аппарата прежде, чем войдет в него, равна нулю. В то же время, проинтегрировав уравнение (5.3) в пределах от 0 до М_о и от 0 до ∞, т.е.

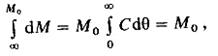
видим, что

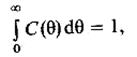
т. е. вероятность того, что частица, вошедшая в аппарат, когда-нибудь из него выйдет, равна единице.

Важнейшими характеристиками случайных величин являются математическое ожидание и дисперсия.

Математическое ожидание определяет среднее значение случайной величины; для времени пребывания частицы в аппарате оно определяется по формуле

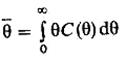
или в размерном виде

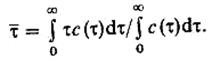
С помощью уравнений (1), (5) и (6) можно определить расход жидкости Q, зная объем аппарата V_a, или, наоборот, зная расход Q, определить неизвестный объем фазы рабочей зоны аппарата V_a.

Дисперсия времени пребывания σ², которая может быть полезной при анализе структуры потока, характеризует среднее значение квадрата разброса его относительно математического ожидания. Дисперсию вычисляют по формуле

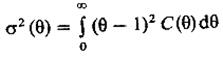
или для размерных значений

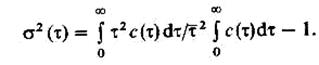
Отметим, что чем больше дисперсия, тем сильнее проявляется продольное перемешивание жидкости.