Рациональные формы поперечных сечений при изгибе

Наиболее рациональным следует признать сечение, обладающее минимальной площадью при заданной нагрузке (изгибающем моменте) на балку. В этом случае расход материала на изготовление балки, будет минимальным. Для получения балки минимальной материалоемкости нужно стремиться к тому, чтобы по возможности наибольший объем материала работал при напряжениях, равных допускаемым или близким к ним. Прежде всего рациональное сечение балки при изгибе должно удовлетворять условию равнопрочности растянутой и сжатой зон балки. Иными словами необходимо, чтобы наибольшие напряжения растяжения (max s_р) н наибольшие напряжения сжатия (max s_с) одновременно достигали допускаемых напряжений [s_р] и [s_с].

Поэтому для балки из пластичного материала (одинаково работающего на растяжение и сжатие: [s_р] = [s_с] = [s]), условие равнопрочности выполняется для сечений, симметричных относительно нейтральной оси. К таким сечениям относится, например, прямоугольное сечение (рис. 9, а), при котором обеспечено условие равенства maxs_р=maxs_с. Однако в этом случае материал, равномерно распределенный по высоте сечения, плохо используется в зоне нейтральной оси. Чтобы получить более рациональное сечение, необходимо возможно большую часть материала переместить в зоны, максимально удаленные от нейтральной оси. Таким образом, приходим к рациональному для пластичного материала сечению в форме симметричного двутавра (рис. 9, б), у которого возможно большая часть материала сосредоточена на полках (горизонтальных массивных листах), соединенных стенкой (вертикальным листом), толщина которой (d) назначается из условий прочности стенки по касательным напряжениям, а также из соображений ее устойчивости (см. гл. 15). К двутаврому сечению близко по критерию рациональности так называемое коробчатое сечение (рис. 9, в).

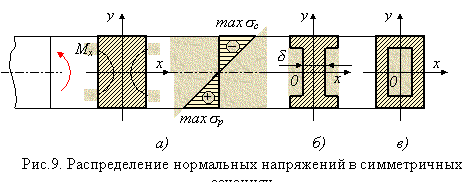
Рассуждая аналогично, приходим к выводу, что для балок из хрупкого материала наиболее рациональным будет сечение в форме несимметричного двутавра, удовлетворяющего условию равнопрочности на растяжение и сжатие (рис. 10):

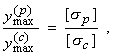
которое вытекает из требования

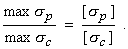
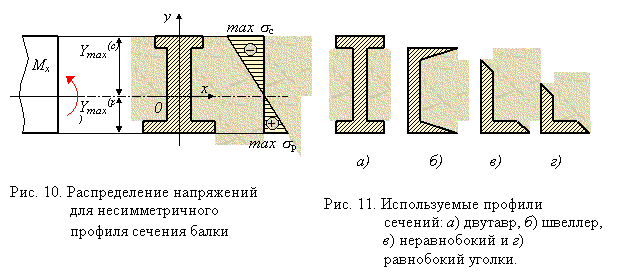
Идея рациональности поперечного сечения стержней при изгибе реализована в стандартных тонкостенных профилях, получаемых методами горячего прессования или прокатки из рядовых и легированных конструкционных высококачественных сталей, а также алюминия и алюминиевых сплавов, получивших широкое распространение в строительстве, машиностроении, авиационном машиностроении. Широко распространены показанные на рис. 11: а - двутавр, б - швеллер, в - неравнобокий уголок, г-равнобокий уголок. Реже встречаются тавр, таврошвеллер, зетовый профиль и др. Употребляются также холодногнутые замкнутые сварные профили.

Поскольку по соображениям технологии сортамент стандартных профилей по размерам ограничен (например, наибольший прокатный двутавр согласно ГОСТ 8239-72 имеет высоту 550 мм), то для больших пролетов приходится применять составные (сварные или клепаные) балки.

15 Составные балки и перемещения при изгибе

Ключевые слова: сварные двутавровые балки, уравнение упругой кривой, прогиб, угол поворота, граничные условия.