Теоретический раздел работы

4.2.1 Определение расстояния от точки до плоскости.

Так как расстояние от точки до плоскости есть ни что иное, как перпендикуляр, проведенный из этой точки к плоскости, то наша задача сводится к проведению этого перпендикуляра. Прямая линия перпендикулярна плоскости, если она перпендикулярна любым двум взаимно пересекающимся прямым этой плоскости. Если в качестве этих прямых взять две любые взаимно пересекающиеся горизонталь и фронталь, то мы можем сказать, что если прямая перпендикулярна плоскости, то ее горизонтальная проекция перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция – перпендикулярна фронтальной проекции фронтали той же плоскости (l ^∑(h; f) → l₁^h₁ Ù l₂^f₂). При этом справедлива и обратная теорема, то есть, если проекция прямой перпендикулярна одноименным проекциям главных линий плоскости, то такая прямая перпендикулярна плоскости (смотри рисунок 4.1)

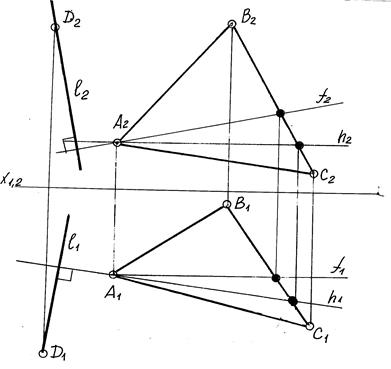
Рисунок 4.1

Рассмотрим применение этих теорем при решении практических задач.

Задача 4.1. Определить расстояние от точки D до плоскости тэта, заданной треугольником АВС.

Ход решения задачи (смотри рисунок 4.2):

- как бы не была задана плоскость, проводим в ней любую фронталь (f₁; f₂) и горизонталь(h₁; h₂);

- из точки D₁ восстанавливаем перпендикуляр к h₁, а из точки D₂ – перпендикуляр к f₂ и получаем направление перпендикуляра l (l₁ l₂);

- находим точку К = l∩Θ (как найти эту точку, смотри задачи на пересечение прямой и плоскости);

- D₁К₁ и D₂ К₂ проекции перпендикуляра. Его натуральную величину находим любым известным способом. В данной задаче его натуральная величина найдена методом треугольник

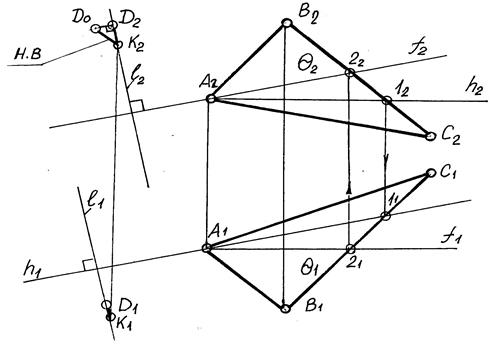
Рисунок 4.2

Часто приходится решать задачу обратную – строить плоскость , которая проходит через заданную точку А перпендикулярно данной прямой (рисунок 4.3). Как правило, эту плоскость задают главными линиями плоскости (горизонталью и фронталью), так как известно направление этих главных линий плоскости. Через точку А проводим горизонталь (ее горизонтальная проекция перпендикулярна горизонтальной проекции прямой и через эту же точку А проводим фронталь плоскости (ее фронтальная проекция перпендикулярна фронтальной проекции прямой).

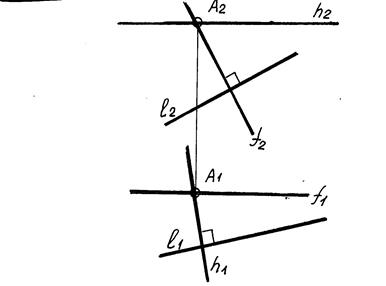
Рисунок 4.3

4.2.2 Параллельность плоскостей

Две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости, параллельны двум пересекающимся прямым другой плоскости. Через точку пространства можно провести пучок прямых линий параллельных данной плоскости.

На комплексном чертеже (эпюре Монжа) (смотри рисунок 4.4) плоскость сигма задана двумя параллельными прямыми и через точку пространства К проведена плоскость, параллельная заданной, при этом прямая g параллельна с, а прямая е параллельна прямым а и в

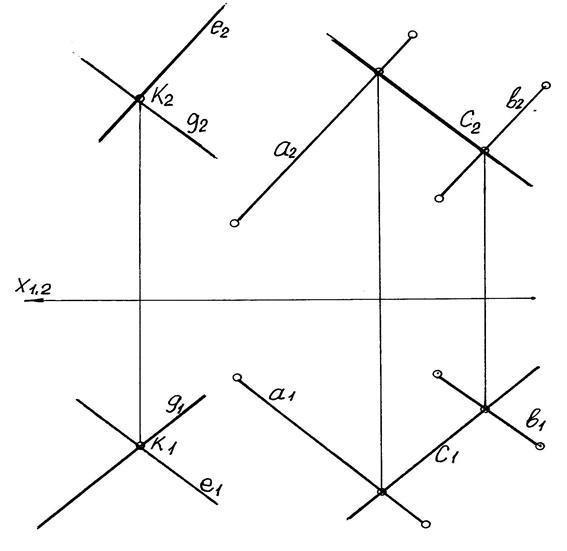
Рисунок 4.4

У параллельных плоскостей их главные линии (следы) соответственно параллельны. На рисунке 4.5 плоскость сигма задана следами и дана точка К, через которую нужно провести плоскость, параллельную плоскости сигма. Для этого через точку К проведем одну из главных линий плоскости (например горизонталь). Через след горизонтали будет проходить новая плоскость сигма.

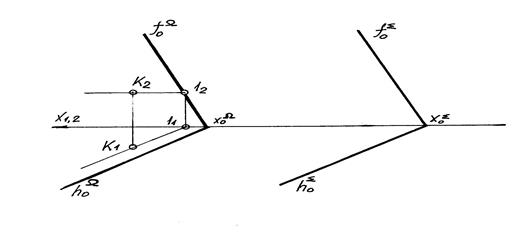
Рисунок 4.5