Общие принципы расчета конструкции

В результате расчета нужно получить ответ на вопрос, удовлет­воряет или нет конструкция тем требованиям прочности и жест­кости, которые к ней предъявляются. Для этого необходимо прежде всего сформулировать те принципы, которые должны быть положе­ны в основу оценки условий достаточной прочности и жесткости.

Методы расчета конструкций выбираются в зависимости от условий работы конструкций и требований, которые к ней предъ­являются. Так, наиболее распространенным методом расчета деталей машин на прочность является расчет по допускаемым на­пряжениям. В основу этого метода положено предположение, что определяющим параметром надежности конструкции является напряжение или, точнее говоря, напряженное состояние в точке. Расчет выполняется в следующем порядке.

На основании анализа напряженного состояния конструкции выявляется та точка сооружения, где возникают наибольшие расчетные (рабочие) на­пряжения 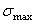. Расчетная величина напряжений сопоставляется с пре­дельно допустимой величиной напряжений 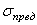для данного материала, полученной на основе предварительных лабораторных испытаний. Чтобы не нарушилась прочность элемента, рабочие напряжения в любой его точке должны быть меньше предельных. Для особо ответственных конструкций, для которых требуется не допускать возникновения пластических деформаций, за величину 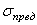принимается 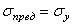. В тех случаях, когда допустимо возникновение пластических деформаций, как правило, принимается 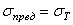. Для хрупких материалов, а в неко­торых случаях и умеренно пластических материалов, принимается .

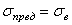Для надежной работы элемента нельзя допустить, чтобы рабочие (расчетные) напряжения в наиболее напряженной точке были близки к предельным, нужно обеспечить запас прочности.

Отношение предельного напряжения для материала, из которого изготовлен элемент конструкции, к максимальному рабочему напряжению называют коэффициентом запаса прочности

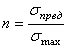. (1.14)

Выбор коэффициента запаса прочности – один из основных и наиболее ответственных этапов расчета на прочность. При заниженном коэффициенте запаса прочности снижается надежность работы детали, повышается опасность ее разрушения при эксплуатации. При завышении запаса прочности увеличивается масса и стоимость детали.

Коэффициент запаса учитывает следующие основные факторы.

1. Погрешности в создании рабочей модели.

2. Возможные превышения, нагрузки в процессе эксплуатации.

3. Степень ответственности изделия.

4. Несовершенства в определении свойств материала.

5. Вероятность возможных экстремальных ситуаций (землетрясение, случайный удар и т.п.).

При назначении коэффициента запаса прочности учитывают, насколько точно можно для проектируемой детали определить рабочее и предельное напряжения. Рабочие напряжения нельзя определить абсолютно точно, так как фактические, действующие на элемент конструкции нагрузки могут существенно отличаться от используемых в расчете. В процессе эксплуатации конструкции возможно кратковременное увеличение нагрузок (перегрузки), часто нагрузки непрерывно изменяются или носят случайный характер (например, нагрузки на крыло летящего самолета). Формулы сопротивления материалов основаны на определенных допущениях, упрощающих расчеты, и, следовательно, не обеспечивают высокой точности. В деталях сложной формы напряжения, как правило, можно определить только приближенно. Предельные напряжения, характеризующие прочность материала, также нельзя определить абсолютно точно вследствие непостоянства химического состава сплавов в различных плавках, отклонений в режимах технологического процесса изготовления материалов, погрешностей при испытании образцов. При расчете элемента конструкции необходимо учитывать возможные последствия его разрушения.

Так как все факторы, влияющие на прочность элемента конструкции, учесть точно в расчете невозможно, в расчет вводят требуемый (допускаемый) коэффициент запаса прочности , гарантирующий надежную работу элемента конструкции в течение требуемого срока службы (табл.1.2)

Таблица 1.2. Ориентировочные значения допускаемого коэффициента

запаса прочности

Вид материала	Характер нагрузки	Коэффициент запаса прочности
Пластичный	Статическая	2,4-2,6
Ударная	2,8-5,0
Повторно-переменная	5,0-15,0
Хрупкий	Статическая	3,0-9,0

Часто этот коэффициент представляют в виде произведения частных коэффициентов запаса 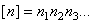, каждый из которых учитывает влияние на прочность элемента конструкции какого-либо одного ил нескольких факторов.

В каждой отрасли машиностроения существуют нормы на допускаемые запасы прочности, основанные на большом опыте расчета деталей и их эксплуатации. Определяемые по нормам коэффициенты запасы прочности называют нормативными.

Прочность элемента конструкции считают обеспеченной, если расчетный коэффициент запаса не меньше допускаемого

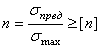. (1.15)

Это равенство называют условием прочности.

Если установлен допускаемый коэффициент запаса прочности и для выбранного материала известно предельное напряжение, определяют максимальное напряжение, которое можно допустить для надежной работы элемента конструкции. Такое напряжение называют допускаемым

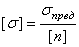. (1.16)

Часто величина допускаемого напряжения берется из таблиц, составленных на основе действующих норм (см. «Справочные данные»).

В практических расчетах считают, что прочность элемента конструкции обеспечена, если возникающие в нем максимальные напряжения не превышают допускаемых. Условие прочности имеет вид

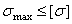. (1.17)

Если материал имеет различные предельные напряжения при растяжении и сжатии, то допускаемое напряжение обозначают соответственно 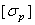и .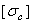

Чтобы уточнить, какое напряжение принято в качестве предельного (предел текучести 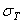или прочности ), иногда в обозначения расчетных и допускаемых коэффициентов запаса прочности вводят соответствующие индексы: ; ; ; .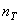

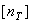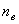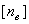Указанный метод является не единственным. Например, на практике в некоторых случаях используется метод расчета конст­рукций по разрушающим нагрузкам. В этом методе путем расчета определяется предельная нагрузка, которую может выдержать кон­струкция, не разрушаясь и не изменяя существенно свою форму. Предельная (разрушающая) нагрузка сопоставляется с проектной нагрузкой, и на этом основании делается вывод о несущей способ­ности конструкции в эксплуатационных условиях.

Условие прочности можно представить в виде

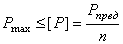, (1.18)

где - коэффициент запаса прочности, принимаемый таким же, как и в методе допускаемых напряжений.

При определении разрушающей нагрузки для конструкций из пластичного материала применяется схематизированная диаграмма напряжений - диаграмма Прандтля (рис.1.9). Схематиза­ция диаграммы заключается в предположении, что материал на на­чальном этапе деформирования находится в упругой стадии вплоть до предела текучести, а затем материал обладает неограниченной площадкой текучести. Материал, работающий по такой диаграмме, называется идеально упруго-пластическим. Такая схема­тизированная диаграмма деформирования в большей степени соот­ветствует действительной диаграмме деформирования материала, имеющего ярко выраженную площадку текучести, т.е. пластичным материалам.

Следует заметить, что определение разрушающей нагрузки возможно только для несложных расчетных схем.

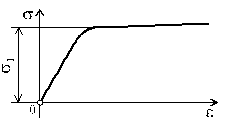
Рис.1.9

Если необходимо добиться наименьших изменений фор­мы конструкции, то производится расчет по допускаемым пе­ремещениям. Это не исключает и одновременной проверки сис­темы на прочность по напряжениям.

В случае расчета конструкции по допускаемым перемещениям необходимо удов­летворять условию

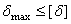, (1.19)

где 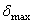и 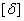- максимальное и допускаемое значения переме­щения.

Для расчета строительных конструкций применяется метод расчета по предельным состояниям.

Данный метод предполагает обеспечить такие условия работы конструкции, при которых исключалась бы возможность наступления расчетного предельного состояния, под которым понимают потерю способности сопротивляться внешним силовым воздействиям или отвечать заданным эксплуатационным требованиям.

Вопросы для самопроверки

- В чем заключаются задачи курса «Сопротивление материалов»?

- Назовите выдающихся русских ученых в области прочности материалов?

- Что называют прочностью, жесткостью, устойчивостью детали?

- Что такое расчетная схема объекта?

- Укажите геометрические признаки стержня, оболочки и массивного тела.

- Какой брус называется призматическим?

- Изложите основные требования при проектировании машин и сооружений?

- Какие силы в сопротивлении материалов считают внешними? Какие силы являются внутренними?

- Какими методами определяют внешние силы? Как называют метод для определения внутренних сил?

- Как классифицируются нагрузки, действующие на части машин и сооружений?

- Что такое сосредоточенная сила, распределенная нагрузка и момент?

- Какие нагрузки принято считать сосредоточенными?

- Какое тело называют брусом? Нарисуйте любой брус и ука­жите ось бруса и его поперечное сечение?

- Какие усилия включают в себя полная система внешних сил?

- Как в сопротивлении материалов располагают систему коор­динат?

- Что в сопротивлении материалов называют внутренними силовыми факторами?

- Перечислите внутренние силовые факторы.

- Перечислите внутренние силовые факторы сечения бруса для общего случая, плоской задачи, линейной задачи?

- Как определяются внутренние силовые факторы через внешние силы?

- Запишите систему уравнений, используемую при определении внутренних силовых факторов в сечении?

- Как обозначается и как определяется продольная сила в сече­нии?

- Как обозначаются и как определяются поперечные силы?

- Как обозначаются и определяются изгибающие и крутящие моменты?

- Какие деформации вызываются каждым из внутренних си­ловых факторов?

- Поясните суть метода сечений.

- Чему равен главный вектор и главный момент внутренних сил?

- Как определяют внутренние силовые факторы?

- Какие основные виды деформаций вызываются внешними силами?

- Типы деформаций.

- Какие возможны виды деформации тела и как они связаны с внутренними силовыми факторами?

- В чём заключается количественная оценка деформаций?

- Перечислите простые виды сопротивление стержня.

- Дайте определение понятия «напряжения» и какие виды напряжения вы знаете?

- В каких единицах измеряются напряжения?

- Чем отличаются нормальные напряжения от касательных?

- Что оценивается величиной напряжений?

- Что такое равнопрочная конструкция?

- Как связаны напряжения в сечении с внутренними силовыми факторами?

- Что называется напряжением? Какая у него размерность?

- Какое напряжение называется нормальным и какое касательным?

- Как связаны напряжения в сечении с внутренними силовыми факторами?

- Как по отношению к площадке направлены нормальные и касательные напряжения? Как они обозначаются?

- Какие напряжения возникают в поперечном сечении при действии продольных сил?

- Какие напряжения возникают при действии поперечных сил?

- Как выражается размерность напряжения в системе СИ и в технической системе?

- Что называется деформацией? Какие деформации называют упругими?

- Какие деформации относятся к простым?

- Какие гипотезы используются при изучении курса «Сопротивление материалов»?

- Что следует понимать под напряженным состоянием в точке?

- Поясните, что такое линейная и угловая деформация.

- Сформулируйте закон Гука и принцип суперпозиции.

- Перечислите основные допущения сопротивления материалов.

- Дайте формулировку принципа Сен-Венана?

- Что называется абсолютным удлинением?

- Что понимается под гипотезой плоских сечений?

- В чем сущность и значение для расчетов принципа малости деформаций?

- В чем заключается принцип независимости действия сил (суперпозиции), при каких условиях этот принцип имеет место, для каких целей применяется?

- Как формулируется закон Гука?

- Что характеризует модуль упругости первого рода? Какова его размерность?

- Что называют абсолютной и относительной линейными деформациями?

- Что такое коэффициент Пуассона?

- Как записывается закон Гука для растяжения (сжатия)?

- В чем различия между деформациями и перемещениями?

- Как определить потенциальную энергию деформации при растяжении (сжатии)?

- Что называют прочностью, пластичностью, упругостью, твердостью материала?

- Что называют пределом пропорциональности, упругости, текучести, прочности (временным сопротивлением) материала?

- Чем характеризуют пластичность материала? По какому признаку материалы делят на хрупкие и пластичные?

- Что такое принцип начальных размеров?

- В чем заключается гипотеза о сплошности и изотроп­ности материалов? Какие тела называются анизотропными?

- Дайте определение нормативного (R_н) и расчетного (R) сопротивления и опишите, как они устанавливаются?

- Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?

- В чем различие между предельным и допускаемым напряжениями?

- Что называется относительной продольной и относительной поперечной деформацией? Для чего они определяются?

- Какие напряжения считают предельными для материалов?

- Что представляет собой коэффициент запаса прочности, с какой целью и как его назначают?

- В чем заключается условие прочности элемента конструкции?

- Как составляют условие жесткости для элементов конструкций?

- В чем основное назначение определения твердости готовых деталей?

- Какие напряжения считают предельными для материалов?

- Что представляет собой коэффициент запаса прочности, с какой целью и как его назначают?

- В чем заключается условие прочности элемента конструкции?

- Что представляет собой допускаемое напряжение? Как его определяют?

- Как составляют условие жесткости для элементов конструкции?

- С какой целью проводятся механические испытания материалов? Какие напряжения являются опасными для пластичных и хрупких материалов?

- Что называется допускаемым напряжением? Как оно выбирается для пластичных и хрупких материалов?

- Что называется коэффициентом запаса прочности и от каких основных факторов зависит его величина?

- Какие три типа расчетов встречаются при расчете прочности конструкций? Напишите условия прочности при растяжении для каждого из этих видов задач?

- Перечислите основные принципы расчета инженерных конструкций.

- Рабочее напряжение, возникающее в детали, равно 160 МПа, а опасное (предельное) напряжение для материала детали 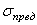=320 МПа. Определить коэффициент запаса прочности?

- Сопротивление материалов – это наука:

1) о действии нагрузок на конструкции;

2) об инженерных методах расчета на прочность, жесткость и устойчивость элементов конструкции;

3) об упругости материальных тел.

- Прочность конструкции

1) способность противостоять коррозии;

2) способность элемента конструкции растягиваться или сжиматься;

3) способность конструкции противостоять внешней нагрузке, не разрушаясь.

- Жесткость конструкции

1) свойство подвергаться технологической обработке;

2) способность конструкции сохранять свои формы и размеры при действии внешней нагрузки;

3) способность противостоять вибрациям.

- Устойчивость конструкции

1) способность сохранять заданную форму упругого равновесия;

2) способность противостоять опрокидыванию;

3) способность возвращаться в исходное положение при нагружении.

- Нормальная работа зубчатого механизма была нарушена из-за возникновения слишком больших упругих перемещений валов. Почему нарушилась нормальная работа передачи?

1) из-за недостаточной прочности валов;

2) из-за недостаточной жесткости валов;

3) из-за недостаточной устойчивости валов.

- Велосипедная спица резко искривилась под действием сжимающей силы. Почему произошло изменение прямолинейной формы спицы?

1) из-за недостаточности прочности;

2) из-за недостаточности жесткости;

3) из-за недостаточности устойчивости.

- При подъеме груза оборвался канат. Что послужило причиной обрыва?

1) недостаточная прочность каната;

2) недостаточная жесткость каната.

- Изменится ли значение внутренних силовых факторов в зависимости от того, будут ли они вычислены по внешним силам, расположенным слева от сечения или справа от него?

1) не изменятся;

2) изменятся.

- Расчетная модель

1) изготовление макета конструкции;

2) изготовление чертежей и эскизов конструкции;

3) совокупность аналогий реального объекта при отбрасывании от него второстепенных подробностей, что упрощает расчет.

- Метод сечений

1) метод определения центра тяжести сечения;

2) метод выявления внутренних сил в сечении нагруженного тела;

3) метод определения сил при растяжении – сжатии.

- Какие внутренние силовые факторы действуют в сечении нагруженного тела?

1) силы растяжения, сдвига, моментов изгиба и кручения;

2) силы молекулярного притяжения;

3) электромагнитные гравитационные силы.

- Главный вектор внутренних сил равен сумме сил внешних, действующих по одну сторону сечения?

1) да;

2) нет;

3) равен главному вектору внешних сил.

- Главный вектор внутренних сил определяется методом сечений?

1) нет;

2) да;

3) определяется аналитически.

- Главный момент внутренних сил определяет моменты изгиба?

1) нет;

2) да;

3) внешние силы.

- Определите вид деформированного состояния бруса, если в его поперечных сечениях возникает изгибающий момент М и растягивающая сила N?

1) чистый изгиб;

2) растяжение;

3) чистый изгиб и растяжение.

- Можно ли с помощью метода сечений определить закон распределения внутренних сил по сечению?

1) можно;

2) нельзя.

- Через любую точку бруса можно провести различные сечения, например, перпендикулярно оси или под углом к ней. Изменится ли величина и направление напряжения в данной точке при изменении направления плоскости сечения?

1) не изменится;

2) изменится.

- В чем состоит принцип независимости действия сил?

1) Деформации конструкций предполагаются настолько малыми, что можно не учитывать их влияние на взаимное расположение нагрузок до любых точек конструкции.

2) Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке.

3) Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности.

4) Поперечные сечения бруса, плоские до приложения к нему нагрузки, остаются плоскими и при действии нагрузки.

- Какие внутренние усилия могут возникать в поперечных сечениях брусьев?

1) ; ;

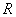2) ; ; ; ; ; ;

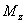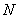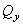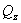3) ; ;

4) ; ; ; ; .

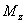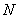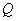- Напряжения нормальные возникают:

1) при растяжении – сжатии и изгибе;

2) при сдвиге – срезе;

3) при статическом нагружении.

- Типы напряжений:

1) при ударе;

2) при ускоренном движении;

3) нормальные ( 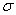), касательные ( ).

- В наклонном сечении нагруженного стержня осевыми нагрузками возникают:

1) силы сдвига;

2) нормальные ( 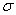) и касательные напряжения ( );

3) продольные деформации.

- При кручении в нормальном сечении вала возникают:

1) касательные напряжения;

2) нормальные напряжения

3) момент сопротивления ( ).

- При чистом изгибе в поперечном сечении балки возникают:

1) поперечные силы (Q);

2) касательные напряжения ( );

3) нормальные напряжения ( ).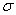

- Какую размерность имеют линейные и угловые деформации?

1) Линейные деформации измеряются в м, а угловые в рад.

2) Линейные и угловые деформации - величины безмерные.

3) Линейные деформации- безмерные величины, а угловые измеряются в рад.

4) Линейные деформации измеряются в м, а угловые деформации безмерные величины.

- Основной метод применяемый для определения внутренних усилий.

1) метод сил,

2) метод перемещений,

3) метод сечений.

- Упругость

1) способность материала изгибаться;

2) способность материала восстанавливать свою форму и размеры после снятия внешней нагрузки;

3) характеристика пружин и рессор.

- Пластичность

1) способность материала приобретать остаточные пластические неисчезающие деформации;

2) свойство пластических масс при нагревании;

3) способность материала при ковке принимать необходимые формы.

- Пластичность характеризуется:

1) пределом пропорциональности;

2) пределом текучести;

3) коэффициентом остаточного удлинения ( ) и остаточного сужения шейки ( ) испытуемого образца.

- Твердость материала:

1) способность материала к механической обработке;

2) способность материала противодействовать механическому проникновению в него инородных (посторонних) тел;

3) свойства, присущие твердым сплавам и алмазу.

- Характеристики механической прочности:

1) модули упругости Е и G;

2) коэффициент Пуассона;

3) пределы пропорциональности 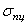, упругости , предел текучести 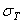, предел прочности .

- Какие механические характеристики материалов вы знаете.

1) коэффициент Пуассона,

2) предел упругости,

3) предел текучести,

4) предел жесткости,

5) предел прочности,

6) предел изогнутости,

7) предел пропорциональности.

- Какие пластические характеристики материалов вы знаете.

1) растянутость,

2) относительное остаточное растяжение,

3) сдвинутость,

4) относительное остаточное сужение.

- Что характеризует допускаемое напряжение.

1) прочность,

2) жесткость,

3) долговечность работы материала.

- Предельные напряжения:

1) напряжения, при которых начинается разрушение (хрупкое и пластичное);

2) напряжение, при котором относительное удлинение составляет 0,5%;

3) напряжение при коэффициенте запаса n= 1.

- Напряжение допускаемое (максимальное), , :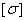

1) всякое напряжение меньше предела пропорциональности;

2) напряжение, равное временному сопротивлению;

3) предельное напряжение, деленное на коэффициент запаса.

- Коэффициент запаса:

1) отношение предельного напряжения к максимальному допустимому напряжению;

2) безразмерная величина больше 1;

3) отношение нормального напряжения к касательному.

- Каковы последствия увеличения коэффициента запаса?

1) вес конструкции уменьшается;

2) вес конструкции увеличивается;

3) вес конструкции не изменяется.

-Коэффициент запаса используют для определения допускаемых напряжений

1) нет;

2) да;

3) для увеличения веса конструкции.

- Справедлив ли закон Гука за пределом пропорциональности

1) нет

2) да, при наклёпе

3) справедлив за пределом прочности

- Коэффициент Пуассона одинаков при растяжении – сжатии

1) да;

2) нет;

3) неодинаков до предела текучести.

- Механические характеристики хрупких и пластичных материалов численно отличаются

1) да,

2) одинаковы при сжатии,

3) неодинаковы при нагревании.

- Предельные напряжения:

1) , ;

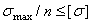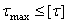2) , ;

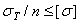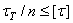3) , .

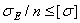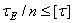- Образцы из стали и дерева с равной площадью поперечного сечением растягиваются одинаковыми силами. Будут ли равны возникающие в образцах усилия?

1) в стальном образце возникнут большие напряжения, чем в деревянном;

2) в образцах возникнут равные напряжения.

- Допускаемое напряжение при расчете на прочность было принято равным 180 МПа. После окончательного выбора размеров конструкции рабочее напряжение стало равным 185 МПа. Грозит ли конструкции опасность разрушения?

1) да;

2) нет.

- Как изменится масса конструкции, если при подборе ее сечения уменьшить коэффициент запаса прочности?

1) масса конструкции уменьшится;

2) масса не изменится.

- Сколько связей накладывается на балку со стороны

1) шарнирно подвижной опоры.

5, 4, 2, 3, 1.

2) шарнирно неподвижной опоры.

5, 4, 2, 3, 1.

3) жесткой заделки.

5, 4, 2, 3, 1.

- Вал находится в равновесии при

1) ,

2) ,

3) ,

4)