Никаких других формул в логике высказываний нет

Определение такого вида называется индуктивным. В п.п. 1 и 2 определены элементарные формулы, в п.п. 3 и 4 даны правила образования новых формул из любых двух данных формул.

Условимся для упрощения записей не заключать в скобки формулы, не являющиеся частями других формул или стоящие под знаком отрицания. Заметим, что в формуле число левых скобок всегда должно быть равно числу правых скобок.

Опишем процедуру формализации высказываний:

1 Если высказывание – простое, то ему ставится в соответствие элементарная формула.

2 Если высказывание – составное, то для составления соответствующей формулы нужно: а) выделить все элементарные высказывания и логические связки, образующие данное составное высказывание; б) заменить их соответствующими символами; в) расставить скобки в соответствии со смыслом данного высказывания.

Пример 8.Определите логическую структуру высказываний (формализуйте высказывания):

1 Е = «Ваш приезд не является ни необходимым, ни желательным».

Составляющие простые высказывания: А = Ваш приезд необходим; В = Ваш приезд желателен. Они соединены между собой неявно имеющимся в высказывании Е союзом «и» и, кроме того, к каждому из них относится частица «не». Таким образом, форма сложного высказывания имеет вид: .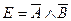

2 Е = «Поиски врага длились уже три часа, но результатов не было, притаившийся враг ничем себя не выдал».

Переформулируем высказывание таким образом, чтобы выделить логические связки, неявно соединяющие простые высказывания: «Если притаившийся враг ничем себя не выдал, то его поиски длились уже три часа и результатов не было». Теперь можно выделить простые высказывания: А = Враг себя выдал; В = Поиски врага длились уже три часа и С = Результат был. Теперь можно формализовать сложное высказывание: .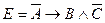

Замечание: Символ импликации ставится там, где подразумевается вторая часть союза «если…, то…», т.е. на месте «то». Таким образом, формула, полученная во втором примере, читается: «Если не А, то В и не С».

3 Е = «Если число делится на 2 и на 3, то оно делится на 6».

В этом высказывании можно выделить следующие элементарные высказывания: А = Число делится на 2, В = Число делится на 3 и С = Число делится на 6. Тогда формула, соответствующая сложному высказыванию, имеет вид: .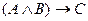

Последний пример наглядно показывает, почему математическую логику интересует только логическая структура высказываний. Точно такую же логическую структуру, как в третьем примере имеет большое количество, например, математических теорем: «Если в четырехугольнике противоположные стороны параллельны и равны, то этот четырехугольник - параллелограмм» или «Если две прямые параллельны третьей прямой, то они параллельны друг другу».

Пример 9. По форме высказываний и выраженным на естественном языке составляющим его простым высказываниям получить фразу на естественном языке.

1 .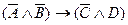

Составляющие простые высказывания:

А = Человек с детства давал нервам властвовать над собой.

В = Человек в юности давал нервам властвовать над собой.

С = Нервы привыкнут раздражаться.

D = Нервы будут послушны.

Для начала прочитаем формулу с использованием логических связок, не обращая внимания на смысл составляющих простых высказываний: «Если не А и не В, то не С и D». Теперь подставим вместо букв соответствующие высказывания, не произнося повторяющиеся части или заменяя их синонимами (местоимениями). Получим следующую фразу на естественном языке:

Е = Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны. (К.Д. Ушинский)

2 .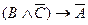

Составляющие простые высказывания:

А = Некто является врачом.

В = Больной поговорил с врачом.

С = Больному стало легче.

Фраза на естественном языке:

Е = Если больному после разговора с врачом не становится легче, то это не врач. (В.М. Бехтерев)

Вычислить значение логического выражения (формулы ЛВ) – значит найти значение истинности этого выражения при заданных значениях истинности составляющих переменных.

При вычислении значения формулы ЛВ логические операции (если нет скобок) вычисляются в определенном порядке:

1) негация (отрицание); 2) конъюнкция; 3) дизъюнкция; 4) импликация и 5) эквиваленция.

Пример 10. Даны формулы. Определить порядок вычисления формул:

1 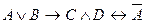. Порядок вычисления следующий:

1) отрицание 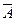; 2) конъюнкция 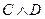; 3) дизъюнкция 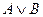; 4) импликация 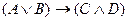и, наконец, эквиваленция .

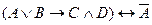2 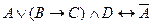. Порядок вычисления следующий:

1) отрицание 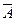; 2) импликация 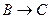; 3) конъюнкция 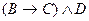; 4) дизъюнкция 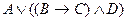; и 5) эквиваленция .

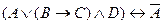Удобной формой записи при нахождении значений формулы, соответствующих всевозможным наборам значений ее переменных, является таблица, которую называют таблицей истинности.

Для начала научимся определять количество строк в таблице. Если высказывание одно, то оно может принимать только два значения истинности – «истина» и «ложь», поэтому строк в такой таблице 3 (две строки для значений переменной и строка заголовка). Примером такой таблицы служит таблица истинности в определении негации. Если переменных в формуле две, то они могут принимать одновременно такие значения: оба высказывания истинны, первое – истинно, а второе – ложно, первое – ложно, а второе – истинно и, наконец, оба они могут быть ложными. Число строк в такой таблице равно 5 (плюс строка заголовка). Вообще, число наборов значений, которые могут принимать п переменных, находится как 2^п.

Сформулируем алгоритм построения таблицы истинности сложного высказывания:

1 Вычислить количество строк и столбцов в таблице истинности.

Пусть в формуле п различных переменных и k операций. Переменные считаем каждую только один раз, а символы операций – все, сколько есть. Тогда число строк в таблице равно 2^п + 1 (число наборов значений переменных плюс строка заголовка), а число столбцов в таблице равно n + k.

2 Начертить таблицу.

3 Заполнить строку заголовка.

В строке заголовка записываем промежуточные формулы, начиная с элементарных и учитывая порядок выполнения операций. Вместо промежуточных формул, если они большие, можно записывать их порядковые номера (из порядка выполнения операций).

4 Заполнить оставшиеся строки таблицы, начиная с первого столбца.

При вычислении значений промежуточных формул, надо помнить, что в каждой операции участвует не более двух формул (может быть и не элементарных).

Пример 11. Составить таблицы истинности для формул: 1) 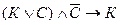; 2) .

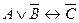1 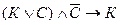. Эта формула содержит 2 различные переменные (К и С) и 4 символа логических операций, т.е. n = 2 и k = 4. Тогда строк в таблице 2² + 1 = 4 + 1 = 5, а столбцов – 2 + 4 = 6. Рисуем таблицу:

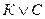Определим порядок выполнения операций: 1) отрицание ; 2) дизъюнкция ; 3) конъюнкция 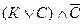и 4) импликация .

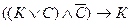Заполняем строку заголовка, начиная с элементарных формул:

К	С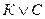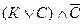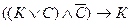

По-другому строка заголовка может выглядеть так:

К	С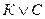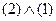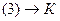

Заполняем первый столбик значениями истинности переменной К, для этого число пустых строк делим пополам (4 : 2 = 2) и в половине пишем значение «истина», а в оставшейся половине – «ложь»:

К	С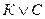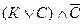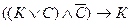

Заполняем второй столбик значениями истинности переменной С. Для этого число пустых строк делим на 4 (4 : 4 = 1) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной К соответствовали оба значения истинности переменной С:

К	С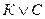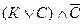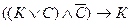

Начиная с третьего столбика, заполняем строки результатами выполнения операций. В третьем столбике записываем результат выполнения операции отрицания . При этом смотрим на соответствующие значения переменной С:

К	С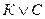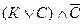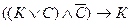

В четвертом столбике записываем результаты выполнения дизъюнкции 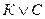, обращая внимание на значения истинности переменных К и С в соответствующей строке:

К	С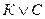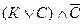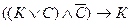

В пятом столбике записываем результаты выполнения операции конъюнкции 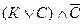. При этом используем значения истинности соответствующих операций из третьего и четвертого столбиков:

К	С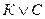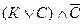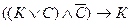

И, наконец, в шестом столбике записываем результаты выполнения итоговой операции импликации 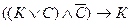, используя результаты предыдущей операции конъюнкции и значения истинности переменной К:

К	С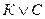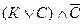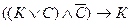

Из итогового результата мы можем сделать следующий вывод: какие бы по смыслу элементарные высказывания не составляли высказывание, соответствующее данной логической структуре, в итоге мы получим истинное высказывание.

Формулы, принимающие значение «истина» при всех наборах значений входящих в нее переменных, называются тождественно истинными или тавтологиями.

Одна из задач математической логики состоит в поиске формул, являющихся тавтологиями и противоречиями (тождественно ложными, т.е. принимающими при всех наборах значений переменных значение «ложь»). Способы рассуждений, формализующиеся тавтологиями, затем применяются при доказательстве утверждений.

2 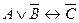. Данная формула содержит 3 различные переменные и 4 символа логических операций. Число строк в таблице – 2³ + 1 = 8 + 1 = 9. Число столбцов – 3 + 4 = 7.

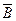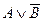Определим порядок выполнения операций: 1) отрицание ; 2) отрицание ; 3) дизъюнкция и 4) эквиваленция 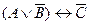. Нарисуем таблицу и заполним строку заголовка, начиная с элементарных формул:

А	В	С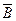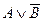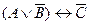

Заполняем первый столбик значениями истинности переменной А, для этого число пустых строк делим пополам (8 : 2 = 4) и в половине пишем значение «истина», а в оставшейся половине – «ложь»:

А	В	С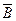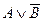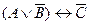

Заполняем второй столбик значениями истинности переменной В. Для этого число пустых строк делим на 4 (8 : 4 = 2) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной А соответствовали по два значения истинности переменной В:

А	В	С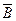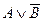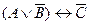

Заполняем третий столбик значениями истинности переменной С. Для этого число пустых строк делим на 8 (8 : 8 = 1) и попеременно записываем в строки по одному значению «истина» и «ложь» таким образом, чтобы каждому значению истинности переменной В соответствовали оба значения истинности переменной С:

А	В	С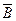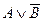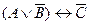

Заполняем четвертый столбик результатами выполнения операции отрицания 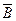. При этом смотрим на значения истинности переменной В в соответствующих строках:

А	В	С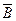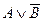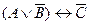

Аналогичным образом заполняем пятый столбик результатами операции отрицания . При этом смотрим на значения истинности переменной С в соответствующих строках:

А	В	С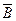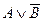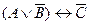

В шестом столбике записываем результаты выполнения операции дизъюнкции 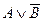. При этом используем значения истинности переменной А и результаты операции 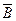(первый и четвертый столбцы):

А	В	С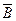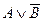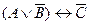

И, наконец, в седьмом столбике записываем результат выполнения итоговой операции эквиваленции 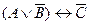. При этом используем результаты предыдущей операции и операции (шестой и пятый столбики):

А	В	С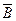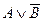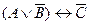

Вывод следующий: истинность высказывания, имеющего данную логическую структуру, зависит от значений истинности составляющих его элементарных высказываний. Формулы такого вида (принимающие при некоторых наборах переменных значение «истина», а при некоторых – значение «ложь») называются выполнимыми (опровержимыми).

С помощью таблиц истинности можно установить, при каких наборах значений истинности входящих переменных формула будет принимать истинное или ложное значение (а также высказывание, имеющее соответствующую логическую структуру), какие формулы будут тавтологиями или противоречиями, а также установить, являются ли две данные формулы равносильными.

В логике говорят, что два предложения равносильны, если они одновременно истинны, либо одновременно ложны. Слово «одновременно» в этой фразе неоднозначно. Так, для предложений «Завтра будет вторник» и «Вчера было воскресенье» это слово имеет буквальный смысл: в понедельник они оба истинны, а в остальные дни недели – оба ложны. Для уравнений «х = 2» и «2х = 4» «одновременно» означает «при одних и тех же значениях переменной». Прогнозы «Завтра будет дождь» и «Неверно, что завтра не будет дождя» одновременно подтвердятся (окажутся истинными) либо не подтвердятся (окажутся ложными). В сущности, это один и тот же прогноз, выраженный в двух разных формах, которые можно представить формулами Х и 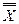. Эти формулы одновременно принимают значение «истина» либо значение «ложь». Для проверки достаточно составить таблицу истинности:

Х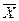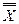

Видим, что значения истинности в первом и последнем столбцах совпадают. Такие формулы, как и соответствующие им предложения, естественно считать равносильными.

Формулы F₁ и F₂ называются равносильными, если их эквиваленция 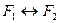– тавтология.

Равносильность двух формул записывается так: 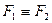(читается: формула F₁ равносильна формуле F₂).

Проверить, равносильны ли формулы, можно двумя способами: 1) составить их эквиваленцию и с помощью таблицы истинности проверить, не является ли она тавтологией; 2) для каждой формулы составить таблицу истинности и сравнить итоговые результаты; если в итоговых столбцах при одинаковых наборах значений переменных значения истинности обеих формул будут равны, то формулы являются равносильными.

Пример 12. Проверить, являются ли формулы 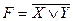и 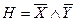равносильными.

Решение.

1 Составим таблицу истинности для формулы F:

Х	Y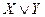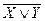

2 Составим таблицу истинности для формулы Н:

Х	Y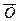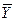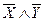

3 Так как итоговые столбцы в обеих таблицах совпадают (совпадают значения формул для одинаковых наборов значений переменных), значит, формулы равносильны, т.е., .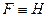

Равносильности формул логики высказываний часто называют законами логики. Перечислим наиболее важные из них:

I 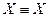1– закон тождества (утверждает, что мысль, заключенная в некотором высказывании, остается (считается) неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует).

II 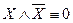– закон противоречия (никакое предложение не может быть истинным одновременно со своим отрицанием).

III 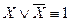– закон исключенного третьего (закон альтернативы).

IV 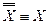– закон двойного отрицания.

V 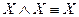; 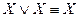– законы тождества (или идемпотентности (на латинском языке «idem» означает «то же», а «potentia» - «сила»)).

VI 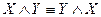; 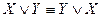– законы коммутативности (переместительности).

VI 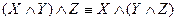; 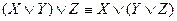– законы ассоциативности (сочетательности).

VII 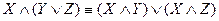; 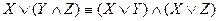– законы дистрибутивности (распределительности).

VIII 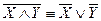; 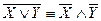– законы де Моргана (английский логик, 1806-1871).

Законы логики используются для упрощения сложных формул и для доказательства тождественной истинности или ложности формул.

Контрольные вопросы

1 Дайте определение высказывания и высказывательной формы.

2 Перечислите основные логические связки.

3 Дайте определение логической операции.

4 Дайте определение негации, конъюнкции, дизъюнкции, импликации и эквиваленции.

5 Какие переменные называются пропозициональными?

6 Сформулируйте определение формулы логики высказываний.

7 Опишите процедуру формализации высказываний.

8 Для чего нужна таблица истинности?

9 Опишите алгоритм составления таблицы истинности.

10 Какие формулы называются тавтологиями, противоречиями, выполнимыми (опровержимыми)?

11 Какие формулы называются равносильными?

12 Сформулируйте несколько основных законов логики.

13 Для чего нужны законы логики?

Тема 4: Элементы комбинаторики

Когда кончается игра в три кости,

То проигравший снова их берет.

И мечет их один в унылой злости;

Другого провожает весь народ…

Данте «Божественная комедия»

Введение

Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.

Комбинаторика как наука возникла в XVI веке. В жизни тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущейся силой в развитии комбинаторики и развивавшейся одновременно с ней теории вероятностей.

Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Н. Тарталья. Он составил таблицу, показывающую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами (например, 1 + 3 + 4 = 4 + 2 + 2).

Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Б. Паскаль и П. Ферма. Исходным пунктом их исследований тоже были проблемы азартных игр. Особенно большую роль сыграла здесь задача о разделе ставки, которую предложил Паскалю его друг шевалье де Мере, страстный игрок. Проблема состояла в следующем: «матч» в орлянку ведется до шести выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а второй – 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив. Применив методы комбинаторики, Паскаль решил задачу в общем случае, когда одному игроку остается до выигрыша r партий, а второму s партий. Другое решение дал Ферма.

Дальнейшее развитие комбинаторики связано с именами Я. Бернулли, Г.Лейбница и Л. Эйлера. Однако и у них основную роль играли приложения к различным играм (лото, солитер и др.). За последние годы комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются при решении транспортных задач, в частности задач по составлению расписаний; для составления планов производства и реализации продукции. Установлены связи между комбинаторикой и задачами линейного программирования, статистики и т.д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории информации.