Локальный экстремум. Достаточные критерии локальных экстремумов

Пусть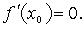

Если f' при переходе через точку x0 меняет знак с "+" на "-", то x0 - точка локального максимума.

Если f' при переходе через точку x0 меняет знак с "-" на "+", то x0 - точка локального минимума.

Если f' при переходе через точку x0 не меняет знака, то точка x0 не является точкой локального экстремума.

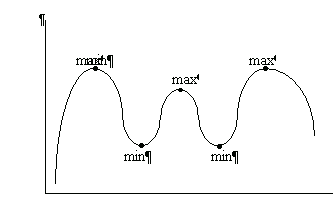
Точки локальных максимума и минимума называются точками локальных экстремумов, а значения функции в них - локальными экстремумами функции.

Пусть функция f (х) определена на отрезке [а, b] и имеет локальный экстремум на каком-то из концов этого отрезка. Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для «а» и левой для «b» полуокрестностью.

II Правило. Пусть f дважды дифференцируема в точке x0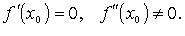

Если 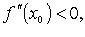то x0 - точка локального максимума.

Если 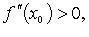то x0 - точка локального минимума.

III Правило. Пусть f n раз непрерывно дифференцируема в точке x0 и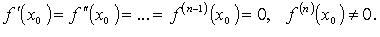

Если n - четное и 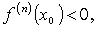то x0 - точка локального максимума.

Если n - четное и 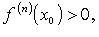то x0 - точка локального минимума.

Если n - нечетное, то x0 не является точкой локального экстремума.

2. Основные теоремы дифференциального исчисления: Ферма

Рассмотрим некоторые теоремы, которые позволят в дальнейшем проводить исследование поведения функций. Они носят названия основных теорем математического анализа или основных теорем дифференциального исчисления, поскольку указывают на взаимосвязь производной функции в точке и ее поведения в этой точке. Рассмотрим теорему Ферма.

Пьер Ферма (1601-1665) - французский математик. По профессии - юрист. Математикой занимался в свободное время. Ферма - один из создателей теории чисел. С его именем связаны две теоремы: великая теорема Ферма (для любого натурального числа n > 2 уравнение хn + yn = zn не имеет решений в целых положительных числах х, у, z) и малая теорема Ферма (если р - простое число и а - целое число, не делящееся на р, то а р-1 - 1 делится на р).

Теорема Ферма. Пусть функция f (х) определена на интервале (а, b) и в некоторой точке х0 (а, b) имеет локальный экстремум. Тогда, если в точке х0 существует конечная производная f '(x0), то f '(x0) = 0.

Доказательство.

Пусть, для определенности, в точке х0 функция имеет локальный минимум, то есть f (х) f (х0), х U(х0). Тогда в силу дифференцируемости

f (х) в точке х0 получим:

при х > х0:

при х < х0:

Следовательно, эти неравенства в силу дифференцируемости имеют место одновременно лишь когда

Теорема доказана.

Геометрический смысл теоремы Ферма: если х0 (а, b) является точкой минимума или максимума функции f (х) и в этой точке существует производная функции, то касательная, проведенная к графику функции

в точке (х0, f (х0)), параллельна оси Ох:

Заметим, что оба условия теоремы Ферма - интервал (а, b) и дифференцируемость функции в точке локального экстремума - обязательны.

Пример 1. у = х, х (-1; 1).

В точке х0 = 0 функция имеет минимум, но в этой точке производная не существует. Следовательно, теорема Ферма для данной функции неверна (не выполняется условие дифференцируемости функции в точке х0).